无缺陷的轴心受压构件,当轴心压力N较小时,构件只产生轴向压缩变形,保持直线平衡状态。若有外界干扰力,构件会产生微小弯曲。当压力N小于临界值,干扰力消失后,构件立即恢复到原来的平衡状态,称为稳定平衡;当压力N达到临界值,干扰力消失后,构件不能恢复到原来的直线平衡状态而转入微弯平衡状态,称为随遇平衡。此时,若压力继续增加,弯曲变形会突然增大,从而使构件丧失承载能力,这种现象称为理想轴心受压构件的屈曲,即理想轴心受压构件丧失了整体稳定性。

在轴心压力作用下如果构件发生屈曲,屈曲变形可能有3种形式:第1种是弯曲变形,构件的轴线由直线变为曲线,如图5.3(a)所示,此时构件的截面只绕一个主轴回转,这种屈曲称为弯曲屈曲;第2种是扭转屈曲,如图5.3(b)所示,各个截面均绕构件纵轴扭转,这种屈曲称为扭转屈曲;第3种是弯扭屈曲,即构件在发生弯曲变形的同时伴有扭转变形,如图5.3(c)所示。轴心受压构件究竟以什么样的形式屈曲,主要取决于截面的形式和尺寸、构件的长度和构件端部的连接条件。

图5.3　轴心受压构件的屈曲变形

轴心受压构件在微弯状态下保持平衡的最小轴心压力,称为欧拉临界力,用Ncr表示,其计算公式为:

式中　E——材料的弹性模量;

I——构件弯曲时截面绕屈曲轴的惯性矩;

l0——受压构件的计算长度或有效长度,l0=μl,l为构件的几何长度,μ称为构件的计算长度系数,由构件两端的支承情况决定,见表5.3。

表5.3　轴心受压构件的临界力和计算长度系数μ

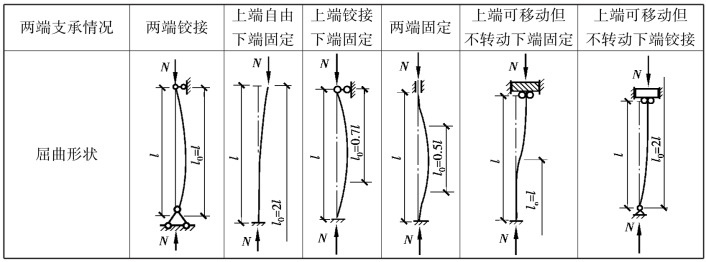
续表

EI代表构件的弯曲刚度,截面的平均应力σcr称为欧拉临界应力,令I=Ai2,得到:(www.daowen.com)

式中　λ——构件的有效长细比;

i——截面的回转半径;

A——构件的毛截面面积。

从式(5.5)中可以看出,构件的临界力Ncr与构件的弯曲刚度EI成正比,与构件的计算长度l0的平方成反比,而与材料的强度无关。因此,构件的稳定性只能用增大截面惯性矩I或减小计算长度l0的办法来提高。

另外,欧拉临界力公式的推导中,假定材料为理想弹塑性体、符合虎克定律,因此当截面应力超过钢材的比例极限fp后,欧拉临界力公式不再适用。此时,可用恩格塞尔(Engesser)提出的切线模量Et=dσ/dε来代替欧拉公式中的弹性模量E,将欧拉公式推广应用于非弹性范围内(图5.4),即改进的欧拉公式:

相应的切线模量临界应力为:

图5.4　切线模量理论

从形式上看,切线模量临界应力公式和欧拉临界应力公式仅Et和E不同,但在使用上却有很大区别。采用欧拉公式时可直接由长细比λ求得临界应力σcr,但是切线模量公式则不能,因为切线模量Et与临界应力σcr互为函数。由于确定切线模量较为困难,在实际使用中非弹性范围的临界应力常采用经验公式进行计算。