1)腹板局部稳定的临界应力

组合梁的腹板同时承受剪应力、弯曲应力和局部压应力的作用,如前所述,在不同的应力状态下,薄板的屈曲各不相同,下面分别讨论在各种应力状态下的临界应力。

(1)剪应力作用下的临界应力

梁支承附近的腹板区段,支承情况为两边简支,两边弹性嵌固于翼缘,主要承受剪应力作用[图4.26(b)],其主压应力大小与剪应力相等但作用方向与剪应力方向成45°角,并引起板的屈曲。如不考虑塑性的发展,在弹性阶段的临界剪应力可用与式(4.54)类似的公式表示为:

式中　b——为板的边长a与h0中较小者;

a——横向加劲肋间距;

h0——腹板高度;

tw——腹板厚度。

屈曲系数k与板的边长比有关(图4.27):

当(a为短边时)

当λs>1.2,临界剪应力处于弹性状态;λs≤0.8,临界剪应力进入塑性状态;0.8<λs≤1.2,临界剪应力处于弹塑性状态。

由图4.27可见,临界剪应力随a/h0的减小而提高,当a/h0>2后,稳定系数变化不大,即如果横向加劲肋的间距大于2h0,对进一步提高临界剪应力的作用不大。因此,《钢结构设计标准》(GB50017—2017)规定:横向加劲肋最大间距为2h0(对无局部压应力的梁,当h0/tw≤100时,可放宽至2.5h0),如图4.28所示。

图4.27　k与a/h0的关系

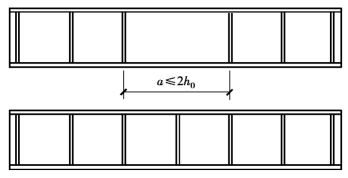
图4.28　横向加劲肋的布置

由式(4.62)—式(4.64)可见,当腹板不设横向加劲肋时,a/h0→∞,k=5.34,若要求τcr≤fv,则λs应不大于0.8,代入式(4.63)得h0/tw=,考虑到区格的平均剪应力一般低于fv,故《钢结构设计标准》(GB50017—2017)规定:

当腹板的高厚比满足式(4.67)时,对仅承受剪应力作用的腹板,不会发生剪切失稳,可不设横向加劲肋。

(2)弯曲应力作用下的临界应力

在弯曲应力作用下,腹板的失稳形式如图4.23(a)所示,凹凸波形的中心靠近压应力合力的作用线。采用与受剪时一样的方法,引入抗弯计算的腹板通用高厚比的概念:

临界应力的计算仍采用式(4.54),但稳定系数的大小取决于板的边长比。图4.29给出了k与a/h0关系,由图可见,当a/h0≥0.7时,k值的变化不大,kmin=23.9,只有当a/h0<0.7后,稳定系数才显著提高,也就意味着只有配置相当密度的横向加劲肋才能提高受弯曲应力时腹板的临界应力。因此,比较有效的措施是在腹板受压区中部偏上的位置设置纵向加劲肋,以便有效地阻止腹板的屈曲。纵向加劲肋只需设置在梁受弯较大的区段。

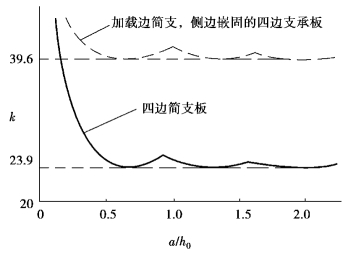
图4.29　薄板受弯时的稳定系数

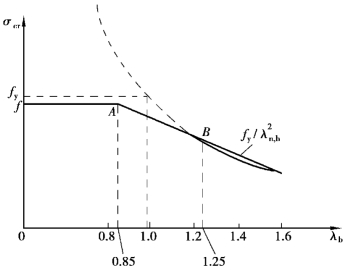
图4.30　临界应力与通用高厚比的关系

由于受拉翼缘刚度很大,梁腹板和受拉翼缘连接边的转动基本上被约束,可认为完全嵌固。受压翼缘对腹板的约束作用除和本身的刚度有关外,还与受压翼缘被限制转动的构造措施有关,当有刚性铺板密铺在受压翼缘上或受压翼缘与钢轨焊接时,受压翼缘的扭转受到约束,取嵌固系数χb=1.66;当受压翼缘扭转没有受到约束时,取嵌固系数χb=1.23。

当梁受压翼缘扭转受到约束时

当梁受压翼缘扭转未受到约束时

为了提高梁的整体稳定性而加强受压翼缘的单轴对称工字形截面梁,受弯时中和轴不在腹板中央,腹板受压区高度hc小于h0/2,此时计算临界应力时,其稳定系数高于23.9,但在实际计算中仍取k=23.9,而把腹板计算高度h0用2hc代替。

当梁受压翼缘扭转受到约束时

当梁受压翼缘扭转未受到约束时

式中　hc——梁腹板弯曲受压区高度,对双轴对称截面,2hc=h0。

根据通用高厚比的范围不同,弯曲临界应力的计算公式为:

当λn,b≤0.85时

当0.85<λn,b≤1.25时

当λn,b>1.25时

式(4.71)中的3个公式分别属于塑性、弹塑性和弹性范围,各范围之间的界线确定原则为:对于没有残余应力和几何缺陷的理想弹塑性板,并不存在弹塑性过渡区,塑性范围和弹性范围的分界点为λn,b=1.0,但由于实际板件内存在缺陷影响,在λn,b<1.0时,临界应力已经开始下降,故《钢结构设计标准》(GB50017—2017)取λn,b=0.85为塑性范围和弹塑性范围的分界点;考虑整体稳定性计算中,当其应力大于0.6fy时,已进入弹塑性范围,相应的,同样的原因《钢结构设计标准》(GB50017—2017)取λn,b=1.25为弹性范围和弹塑性范围的分界点。临界应力和通用高厚比的关系曲线如图4.30所示。

(3)局部压应力作用下的临界应力

在集中荷载作用处未设置支承加劲肋及吊车荷载作用的情况下,腹板将处于局部压应力的作用,其应力分布状态如图4.23(c)所示,在上边缘处最大,下边缘处为零。用于腹板抗局部压应力作用的通用高厚比为:

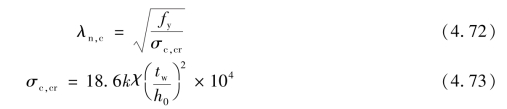
承受局部压应力时翼缘板对腹板的嵌固系数:

稳定系数k与板的边长比有关:

局部压应力和弯曲应力均为正应力,但腹板中引起横向非弹性变形的残余应力不如纵向的大,故取λn,c=1.2作为弹塑性影响的下起始点,偏于安全取λn,c=0.9为弹塑性影响的上起始点。(www.daowen.com)

根据临界屈曲应力不小于屈服应力的准则,按a/h0=2考虑,得到不发生局部压应力失稳的腹板高厚比限值为:

规范偏于安全取:

如不满足这一条件,应减小横向加劲肋的间距,或设置短加劲肋。

2)腹板加劲肋的设置

组合梁腹板配置加劲肋应符合下列规定:

④任何情况下,h0/tw均不应超过250。

⑤梁的支座处和上翼缘受较大固定集中荷载处,宜设置支承加劲肋。

⑥腹板的计算高度h0应按下列规定采用:对轧制型钢梁,为腹板与上、下翼缘相接处两内弧起点间的距离;对焊接截面梁,为腹板高度;对高强度螺栓连接(或铆接)梁,为上、下翼缘与腹板连接的高强度螺栓(或铆钉)线间最近距离。

3)不考虑腹板屈曲后强度的腹板局部稳定性验算

①仅配置横向加劲肋的腹板[图4.31(a)],其各区格的局部稳定应按式(4.79)计算:

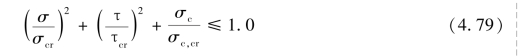
式中　σ——所计算腹板区格内由平均弯矩产生的腹板计算高度边缘的弯曲压应力,N/mm2;

τ——所计算腹板区格内由平均剪力产生的腹板平均剪应力,N/mm2,应按τ=V/(hwtw)计算,hw为腹板高度;

σc——腹板计算高度边缘的局部压应力,N/mm2,应按式(4.7)计算,但取式中的ψ=1.0;

τcr,σcr,σc,cr——各种应力单独作用下的临界应力,N/mm2。

②同时用横向加劲肋和纵向加劲肋加强的腹板[图4.31(b)、(c)],其局部稳定性应按下列公式计算:

•受压翼缘与纵向加劲肋之间的区格

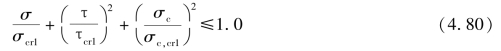
σcr1,σc,cr1,τcr1分别按下列方法计算:

a.σcr1按式(4.71)计算,但式中的λn,b改用下列λn,b1代替。

当梁受压翼缘扭转受到约束时

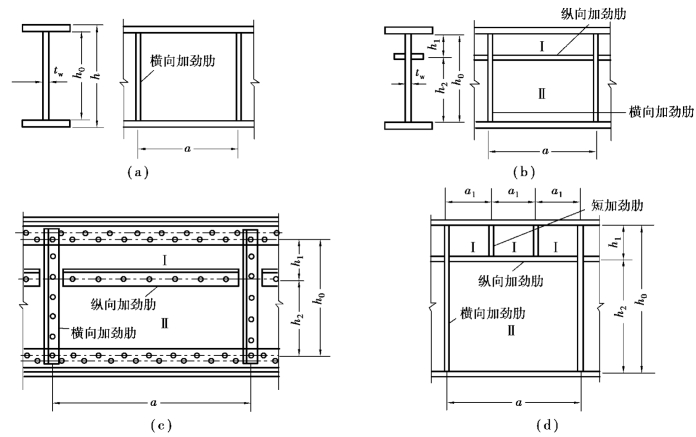
图4.31　腹板加劲肋的布置

式中　σ2——所计算区格内由平均弯矩产生的腹板在纵向加劲肋处的弯曲压应力,N/mm2;

σc2——腹板在纵向加劲肋处的横向压应力,取0.3σc。

a.σcr2按式(4.71)计算,但式中的λn,b改用式(4.84)中的λn,b2代替。

b.τcr2按式(4.62)—式(4.66)计算,将式中的h0改为h2(h2=h0-h1)。

c.σc,cr2按式(4.77)计算,将式中的h0改为h2,当a/h2>2时,取a/h2=2。

③在受压翼缘与纵向加劲肋之间设有短加劲肋的区格[图4.31(d)],其局部稳定性按式(4.80)计算。

该式中的σcr1按与式(4.80)相同的方法计算;τcr1按式(4.62)—式(4.66)计算,但将式中的h0和a改为h1和a1(a1为短加劲肋之间的间距);σc,cr1按式(4.77)计算,但式中的λn,c改用下列λn,c1代替。

当梁受压翼缘扭转受到约束时

当0.8≤λn,s≤1.2时

当λn,s≥1.2时

式中　M,V——所计算同一截面上梁的弯矩设计值(N·mm)和剪力设计值(N)。计算时,V≤0.5Vu,取V=0.5Vu;当M≤Mf时,取M=Mf;

Mf——梁两翼缘所能承担的弯矩设计值,N·mm;

Af1,hm1——较大翼缘的截面积(mm2)及其形心至梁中和轴的距离(mm);

Af2,hm2——较小翼缘的截面积(mm2)及其形心至梁中和轴的距离(mm);

αe——梁截面模量考虑腹板有效高度的折减系数;

Wx——按受拉或受压最大纤维确定的梁毛截面模量,mm3;

Ix——按梁截面全部有效算得的绕x轴的惯性矩,mm4;

hc——按梁截面全部有效算得的腹板受压区高度,mm;

γx——梁截面塑性发展系数;

ρ——腹板受压区有效高度系数;

λn,b——用于腹板受弯计算时的正则化宽厚比;

λn,s——用于腹板受剪计算时的正则化宽厚比。

当焊接截面梁仅配置支座加劲肋时,取=0。