薄板在荷载作用下(图4.24),当荷载达到一定值时,板由平面状态变为微微弯曲状态,根据弹性力学小挠度理论,其挠度w随x和y两个坐标值而变,薄板的屈曲为:

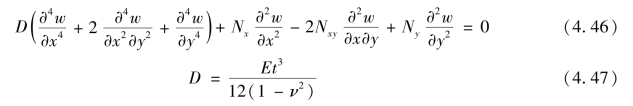
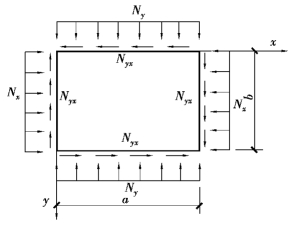
图4.24　荷载作用下的板

式中　D——板单位宽度的抗弯刚度,也称为柱面刚度;

t——板厚;

ν——钢材的泊松比,取0.3。

对于图4.22所示的四边简支板,在单向荷载作用下,微分方程可简化为:

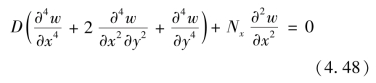
其解可用双重三角级数表示如下:

式中　m——板屈曲时沿x方向的半波数;

n——板屈曲时沿y方向的半波数。

其边界条件为,当x=0和x=a及y=0和y=a时,挠度和弯矩均为零,即

将式(4.49)和式(4.50)代入式(4.48)得微分方程的解为:(www.daowen.com)

从式(4.51)可见,当n=1时,即板屈曲时在y方向形成一个半波时,其临界力Nxcr最小。

式中,称为稳定系数,与板的边界条件(支承情况)和板所受荷载情况有关。

将D,E=2.06×105N/mm2及ν=0.3代入式(4.52)并改用临界应力来表达得:

考虑到梁受力时,并不是所有的板件同时屈曲,板件之间存在相互约束作用,在式(4.53)中引入约束系数χ。

当m取不同值时,将k与a/b的关系绘成曲线,如图4.25所示。当a/b>1时,板屈曲成几个半波,只有当a/b<1时,其临界压力才有可能得到提高,系数k随a/b变化,但各条曲线均接近最小值kmin=4.0。对于其他支承和荷载情况,可推导出与式(4.54)相同的形式,但k的表达式不同。表4.3给出了四边简支板受弯的k值。

图4.25　k与a/b的关系

表4.3　四边简支薄板受弯时的稳定系数k值

注:b为板的受载边宽度。