当符合下列3种情况之一时,可不计算梁的整体稳定性:

①有铺板(各种钢筋混凝土板和钢板)密铺在梁的受压翼缘上并与其牢固相连,能阻止梁受压翼缘的侧向位移时。

②当箱形截面简支梁符合第①条的要求或其截面尺寸(图4.10)满足h/b0≤6,l1/b0≤95时,l1为受压翼缘侧向支承点间的距离(梁的支座处视为有侧向支承)。

图4.10　箱形截面

③H型钢或工字形截面简支梁受压翼缘自由长度l1与其宽度b1之比不超过表4.1所列数值时。

表4.1　H型钢或工字形截面简支梁不需验算整体稳定性的最大l1/b1值

对不满足上述不必验算整体稳定的条件时,需进行整体稳定性验算。

•《钢结构设计标准》(GB50017—2017)规定的计算方法

为保证梁不发生整体失稳,其临界应力应不超过弯曲应力,即

考虑材料的抗力分项系数:

式中,φb=σcr/fy为梁的整体稳定系数,按附录10计算。对于工字形截面梁有:

《钢结构设计标准》(GB50017—2017)规定的梁整体稳定验算方法:(www.daowen.com)

单向受弯构件

双向受弯构件

上述整体稳定系数的计算是按弹性理论方法计算的。研究表明,当按式(4.19)算得的φb大于0.6时,梁已进入弹塑性工作阶段,其整体稳定的临界力有明显下降,必须对φb进行修正。《钢结构设计标准》(GB50017—2017)规定,当按式(4.19)算得的φb大于0.6时,应用式(4.22)计算的φ′b代替φb值进行梁的整体稳定性验算:

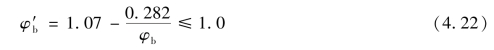
•《公路桥梁钢结构设计规范》(JTGD64—2015)规定的计算方法

在桥梁钢结构中,由于制造安装等原因,实际钢结构不可避免地存在结构与荷载的初偏心和残余应力等,实际钢桥的失稳破坏为弹塑性极值稳定问题。由于影响弹塑性极值稳定的因素很多,计算复杂,钢结构的实际失稳临界应力难以通过计算求得。为了解决钢桥的整体稳定设计问题,许多研究者在整体稳定性验算中主要考虑梁在作用于其平面内的弯矩单独作用下,构件呈现弯扭失稳时的整体稳定折减系数。为保证梁不发生整体失稳,当等截面钢梁不满足可不计算梁整体稳定性的要求时,应按《公路桥梁钢结构设计规范》(JTGD64—2015)中有关梁的整体稳定验算公式进行梁整体稳定的计算。

单向受弯时

双向受弯时

Wx,eff,Wy,eff——有效截面相对于x轴和y轴的截面模量,其中受拉翼缘仅考虑剪力滞影响,受压翼缘同时考虑剪力滞和局部稳定影响;

Mcr,x,Mcr,y——两个主平面内弯矩单独作用下,考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩,可采用有限元方法计算。

【例4.1】　对均布荷载作用下热轧工字钢简支梁的强度、刚度和整体稳定性验算。热轧工字钢简支梁的计算跨径l=6m,截面采用I36a,梁上作用均布荷载设计值q=30kN/m,荷载标准值qk=23kN/m。该梁为顶棚次梁,未设加劲肋,跨中设置侧向支承,钢材为Q235,恒载分项系数γG=1.2。