简而言之,整体稳定性就是指结构或构件在荷载作用下能保持稳定的能力。钢梁同钢筋混凝土梁相比,为了充分发挥钢材的强度,其截面常设计成高而窄的形式,如图4.8所示的工字形截面梁,荷载作用在梁截面主轴y—y且通过其弯曲中心,梁在最大刚度平面内绕主轴x—x弯曲,梁处于平面弯曲状态。梁在弯矩作用下,上翼缘受压、下翼缘受拉、腹板部分受压部分受拉,梁犹如受压构件和受拉构件的组合体。虽然受压的上翼缘在压应力作用下,可能沿刚度较小的翼缘板平面外屈曲,但由于腹板和受拉的下翼缘在这个方向提供了连续的抗弯和抗剪约束,使其不可能发生平面外的屈曲。当外荷载增大到一定数值时,受压翼缘所受到的压应力将使翼缘板绕自身的强轴发生平面内的屈曲,对整个梁来说发生了侧向位移,并带动腹板和受拉的下翼缘发生侧向位移,由于受拉的下翼缘对这个侧向位移的约束作用,使整个截面发生侧向位移的同时,伴随着整个截面的扭转,继而丧失继续承载的能力,这种现象称为梁的弯扭屈曲或整体失稳,如图4.9所示。梁整体失稳时的最大弯矩称为临界弯矩,对应的应力称为临界应力。在梁所承受的弯矩达到临界弯矩之前,梁在弯矩作用平面内发生弯曲;当达到临界弯矩时,梁突然发生弯矩平面外的位移和扭转。如果临界应力低于屈服点,属于弹性弯扭失稳,可采用弹性稳定理论通过在梁失稳后的位移建立平衡微分方程的方法求解。

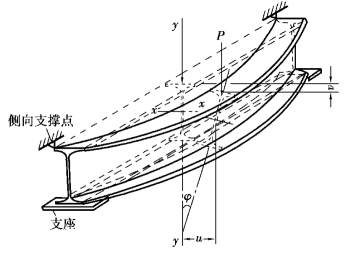
图4.8　钢梁丧失整体稳定性的现象

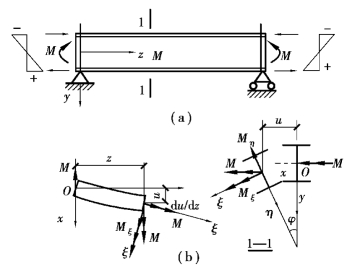
图4.9　工字形截面简支梁整体弯扭失稳

根据弹性稳定理论,双轴对称工字形等截面梁的临界荷载、临界弯矩和受压翼缘的临界应力分别为:

从以上临界弯矩的计算可见:

①截面的侧向刚度EIy、抗扭刚度GJ和翘曲刚度EIw越大,临界弯矩越高。

②梁两端约束程度越高,临界弯矩越高;构件侧向支承点间的间距l1越小,临界弯矩越大。(www.daowen.com)

③梁的整体失稳是由于受压翼缘侧向弯曲引起的,受压翼缘越宽大的截面,其临界弯矩越高。

④荷载的类型和作用位置对临界弯矩的影响,弯矩图越饱满,受压翼缘所受到的压应力越高,其临界弯矩越小;荷载作用在梁的上翼缘,当梁发生扭转时,将加剧扭转,助长屈曲,降低临界弯矩;反之,当荷载作用在梁的下翼缘时,将减缓扭转,提高临界弯矩。

为了提高梁的整体稳定性,可采取以下措施:

①加宽受压翼缘板,可使Ix和Iy都得到提高。

②增加横向联系,减小梁的侧向计算长度l1。

③当梁内无法增设侧向支撑时,宜采用闭合的箱形截面,工字形截面、槽形、T形截面次之,避免选用L形截面。

④增加梁两端的约束提高其整体稳定性。

⑤减少初始变形、初始偏心、残余应力等初始缺陷。