根据试验,一般的低碳钢和低合金钢试件受弯时,其工作性能同简单的拉伸试验,可视为理想的弹塑性材料,应变符合平截面假定。因此,在静力荷载作用下,随着荷载的增加,梁弯曲应力的发展过程可分为3个阶段。以双轴对称工字形截面梁为例说明如下。

1)弹性工作阶段

荷载较小时,截面上各点的应力和应变都呈三角形分布,应力与应变成正比关系,截面上下边缘的最大应力均小于钢材的屈服强度fy[图4.4(b)],荷载继续增加,截面边缘纤维应力达到屈服强度fy,此时的弯矩即为梁弹性工作阶段的最大弯矩:

式中　Wn——梁的净截面抵抗矩,或称梁的截面模量。

对于需要计算疲劳和直接承受动力荷载的梁,常采用弹性方法设计,因此Me是《钢结构设计标准》(GB50017—2017)中直接承受动力荷载的钢梁抗弯强度计算的依据,也是《公路钢结构桥梁设计规范》(JTGD64—2015)中抗弯强度计算的依据。

2)弹塑性工作阶段

当梁边缘的最大正应力达到屈服点时,梁的承载力还远没有达到其极限承载力。随着荷载的进一步增加,由于钢材的塑性性质,边缘纤维进入屈服阶段,应力保持不变,应变继续增大,此时,在截面的上、下各有一个高为a的区域,在这个区域内,应变仍符合平截面假定,但应力不再随着应变的增加而增加,而是保持不变,形成塑性区[图4.4(c)],梁处于弹塑性工作阶段,此时截面内对应的弯矩值即为《钢结构设计标准》(GB50017—2017)中承受静力荷载或间接承受动力荷载的钢梁抗弯强度计算的依据。

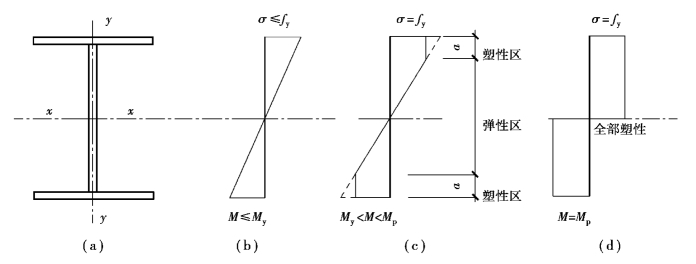
图4.4　各受力阶段梁截面上的正应力分布

3)塑性工作阶段(www.daowen.com)

随着荷载的进一步增大,塑性区不断发展,弹性区不断减小。由于截面内部弹性区的约束,截面塑性区的塑性变形不能自由发展,钢梁仍能承受更大的荷载作用。当弹性区减小至完全消失时[图4.4(d)],荷载不再增加,而变形继续发展,形成“塑性铰”,梁的承载力达到极限承载力,此时的弯矩称为梁塑性弯矩。

式中　S1n,S2n——分别为中和轴以上及以下净截面面积对中和轴的面积矩;

Wpn——梁的净截面塑性抵抗矩,Wpn=S1n+S2n。

梁的塑性弯矩与弹性弯矩之比为:

γF称为截面的形状系数,与截面的几何形状有关,而与所用材料无关。一般截面的形状系数如图4.5所示。

图4.5　截面形状系数

钢结构设计计算中,若全部采用弹性弯矩,则偏于保守;若全部采用塑性弯矩,虽然可以获得较大的经济效益,但过大的塑性变形将使其不适于继续承载,不能满足刚度要求。故《钢结构设计标准》(GB50017—2017)规定:对于不直接承受动力荷载的固端梁、连续梁以及实腹式构件组成的单层和两层框架结构,可以采用塑性设计(即以塑性弯矩为极限弯矩);对需计算疲劳的梁,采用弹性设计;除以上两类构件外,一般的静定梁可以有限制地利用塑性,取截面的塑性发展深度a≤0.125h,采用塑性部分深入截面的弹塑性工作阶段作为设计准则。γx,γy是考虑塑性部分深入截面的系数,称为截面塑性发展系数,γx,γy的取值见附录3。