1)角焊缝计算的基本公式

直角角焊缝有两种计算方法:一种是世界各国多年习用的不考虑角焊缝受力方向的单一应力法;另一种是近年来国际上采用的考虑角焊缝受力方向对焊缝承载力影响的折算应力法。后一种计算方法经过针对我国钢材和焊接工艺条件进行的试验,证明了新公式的可靠性,已纳入现行《钢结构设计标准》(GB50017—2017)中。两种计算方法的主要区别在于对角焊缝有效截面上的应力状态采用的假定不同,因而分析和计算方法也不同。按原方法的应力分析,虽然在轴心力作用下侧焊缝和端焊缝在有效截面上的应力状态不一样,但为了计算方便,假定有效截面上只按均布的单一的角焊缝剪应力控制。按新方法的应力分析,端焊缝能提高22%的承载力,但端焊缝的刚度较大,有脆断倾向。故规范规定:对于承受静载或间接承受动载的连接,宜用新的计算方法,而对于直接承受动载的连接仍采用原来的计算方法。但两种方法均用同一算式,只是对端缝的强度增大系数β取值不同,详见于后。

如图3.29(a)所示的角焊缝连接,在外力Nx作用下角焊缝有效截面(helw=0.7hflw)上产生的应力σ⊥和τ⊥分别为垂直于焊缝长度方向的正应力和剪应力,如图3.29(b)所示。在外力Ny的作用下产生的τ‖为平行于焊缝长度方向的剪应力。三向应力作用于一点,则该点处于复杂应力状态。根据理论分析和试验,可按第四强度理论来计算。该三向应力相互垂直,其强度条件表达式为:

式中　——角焊缝的强度设计值(即侧面焊缝的强度设计值),见附表1.2。相当于焊缝单向抗拉强度设计值。

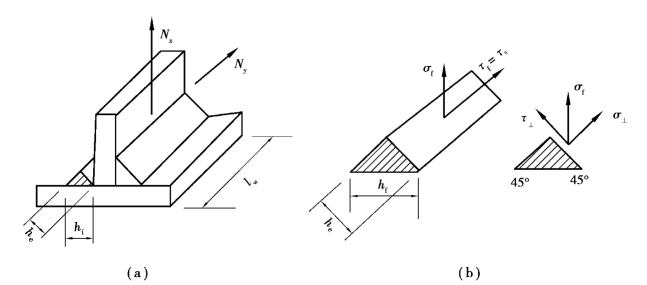
图3.29　角焊缝有效截面上各种应力

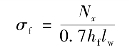
现将式(3.5)转换为便于使用的计算式。如图3.29(b)所示,令σf为垂直于焊缝长度方向按焊缝有效截面计算的应力:将σf分解为正应力σ⊥和剪应力τ⊥:,又把τ‖改称为τf,则τf=τ‖=。将上述σ⊥,τ⊥,τf代入式(3.9)中,得

式中　σf——按焊缝有效截面计算,垂直于焊缝长度方向的应力,N/mm2;

τf——按焊缝有效截面计算,沿焊缝长度方向的剪应力,N/mm2;

he——直角角焊缝的计算厚度(mm),当两焊件间隙b≤1.5mm时,he=0.7hf;1.5mm<b≤5mm时,he=0.7(hf-b),hf为焊脚尺寸;

lw——角焊缝的计算长度(mm),根据具体情况进行折减:若未加引弧板,则两面侧焊的每条焊缝的计算长度等于其实际长度减去2倍的焊脚尺寸,即lw=l-2hf;三面围焊的正面角焊缝计算长度则无须折减,两条侧面角焊缝的计算长度等于其实际长度减去1倍的焊脚尺寸,即lw=l-hf;

——角焊缝的强度设计值,N/mm2;

βf——正面角焊缝的强度设计值增大系数:对承受静力荷载和间接承受动力荷载的结构,βf=1.22;对直接承受动力荷载的结构,βf=1.0。

式(3.10)就是角焊缝连接计算的基本公式,由该公式可知:对正面焊缝,当只有垂直于焊缝长度方向的轴心力Nx时(Ny=0),应满足

对侧面焊缝,当只有平行于焊缝长度方向的轴心力Ny时(Nx=0),应满足:

对于承受静力荷载或间接承受动力荷载的结构,采用上述公式并令βf=1.22。对于直接承受动力荷载的结构,正面焊缝强度虽高,但应力集中现象较严重,又缺乏足够的研究,故规定取βf=1.0。

在公路桥梁钢结构设计中一般不考虑正面角焊缝强度设计值的提高,通常取βf=1.0,并引入结构重要性系数,得到《公路钢结构桥梁设计规范》(JTGD64—2015)中的直角角焊缝在各种应力综合作用下,作用力N与焊缝长度平行以及作用于N与焊缝长度垂直的计算公式,见式(3.13)—式(3.15)。

直角角焊缝在各种力综合作用下,σf和τf共同作用处的计算公式,整理后可得

作用力N与焊缝长度平行,此时垂直于焊缝长度方向的应力σf=0,则

作用力N与焊缝长度垂直,此时平行于焊缝长度方向的应力τf=0,则

式中　——公路钢结构桥梁设计时采用的角焊缝抗拉、抗剪强度设计值。

当角焊缝承受斜向轴心力N时(图3.30),N与焊缝成角θ,应先把N分解为Nx(垂直于焊缝长度)和Ny(平行于焊缝长度),并求出相应的应力σf和τf。

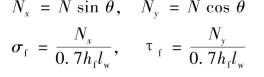
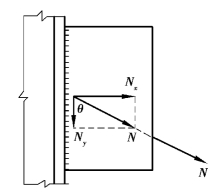
图3.30　角焊缝倾斜受力

再将σf和τf代入基本公式,即可直接进行强度计算,也可以经过整理按式(3.16)计算:

图3.31(b)所示为矩形拼接板,正面角焊缝连接。此时,外力与焊缝长度方向垂直,可按式(3.18)计算,桥梁钢结构则不考虑正面角焊缝的强度增大系数。

图3.31(c)所示为矩形拼接板,三面围焊。可先按式(3.18)计算正面角焊缝所承担的内力N1,再由N-N1按式(3.17)计算侧面角焊缝。

如三面围焊受直接动载,由于βf=1.0,则按轴力由连接一侧角焊缝有效截面面积平均承担计算:

式中　∑lw——连接一侧所有焊缝的计算长度之和。

为使传力线平缓过渡,减小矩形拼接板转角处的应力集中,可改用菱形拼接板,如图3.31(d)所示。菱形拼接板正面角焊缝长度较小,为简化计算,可忽略正面角焊缝及斜焊缝的βf增大系数,不论何种荷载均按式(3.18)计算。

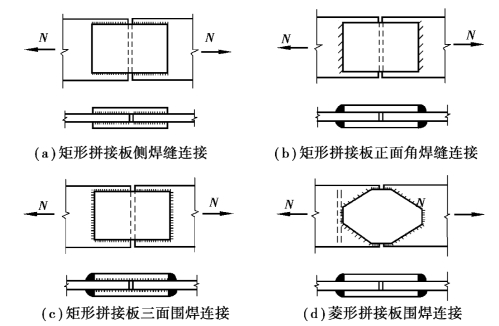
图3.31　轴心力作用下角焊缝连接

(2)受轴心力角钢的连接

①当用侧面角焊缝连接角钢时,虽然轴心力通过角钢截面形心,但肢背焊缝和肢尖焊缝到形心的距离e1≠e2[图3.32(a)],受力大小不等。设肢背焊缝受力为N1,肢尖焊缝受力为N2,由平衡条件得:

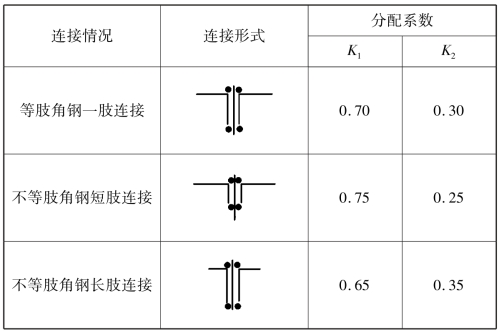
式中　K1,K2——角钢肢背、肢尖焊缝内力分配系数,见表3.3。

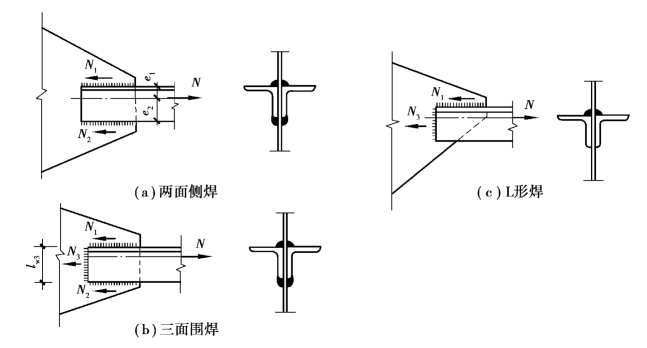
图3.32　角钢角焊缝上受力分配

表3.3　角钢角焊缝的内力分配系数

按下式验算肢背、肢尖焊缝强度:

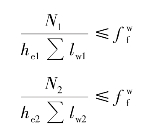
式中　he1,he2——分别为肢背、肢尖焊缝有效厚度;

∑lw1,∑lw2——分别为肢背、肢尖焊缝计算长度之和。

②当采用三面围焊[图3.32(b)]时,可选定正面角焊缝的焊脚尺寸hf,并算出它所能承担的内力:

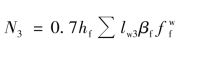
再通过平衡关系,可以解得:

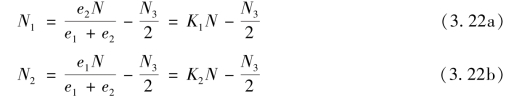
对于L形的角焊缝[图3.32(c)],同理求得N3后,可得

根据上述方法求得N1,N2以后,再按式(3.19)计算侧面角焊缝。

(3)弯矩作用下角焊缝计算

当力矩作用平面与焊缝群所在平面垂直时,焊缝受弯,如图3.33所示。弯矩在焊缝有效截面上产生和焊缝长度方向垂直的应力σf,此弯曲应力呈三角形分布,边缘应力最大,图3.33(b)给出焊缝有效截面,计算公式为

式中　Ww——角焊缝有效截面的截面模量。

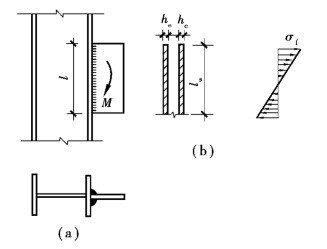
图3.33　弯矩作用时角焊缝的应力

(4)扭矩作用下角焊缝计算

①焊缝群受扭。当力矩作用平面与焊缝群所在平面平行时,焊缝群受扭,如图3.34所示。计算时采取下述假定:被连接件在扭矩作用下绕焊缝有效截面的形心O旋转,焊缝有效截面上任一点的应力方向垂直于该点与形心O的连线,应力大小与其到形心距离r成正比。按上述假定,焊缝有效截面上距形心最远点应力最大,为:

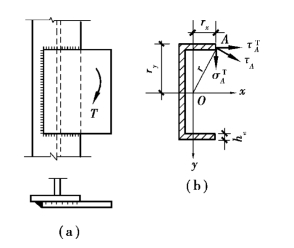
图3.34　扭矩作用时角焊缝的应力

式中　J——焊缝有效截面[图3.29(b)]绕形心O的极惯性矩J=Ix+Iy,Ix,Iy分别为焊缝有效截面绕x,y轴的惯性矩;

r——距形心最远点到形心的距离;

T——扭矩设计值。(www.daowen.com)

式(3.25)给出的应力与焊缝长度方向成斜角记为τA,它不便与其他应力叠加,因此需将它分解到x轴方向(沿焊缝长度方向)和y轴方向(垂直焊缝长度方向)的分应力,即为:

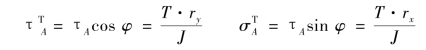
rx,ry,x,r如图3.29(b)所示,将代入式(3.10),可得设计公式为:

②环焊缝受扭(图3.35)。扭矩作用下环形角焊缝有效截面只有剪应力沿切线方向(环向)作用,计算公式为:

式中　J——焊缝环形有效截面极惯性矩,焊缝有效厚度he<0.1D时,J≈0.25πheD3;

D——可近似地取为管的外径。

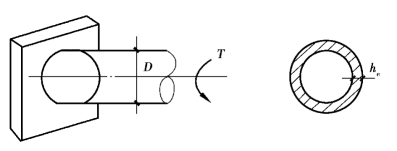
图3.35　环形焊缝受扭

(5)弯矩、剪力、轴力共同作用下角焊缝计算

将连接(图3.36)所受水平力N、垂直力V平移到焊缝群形心,得到一弯矩M=V·e、剪力V和轴力N。弯矩作用下,焊缝有效截面上的应力为三角形分布,方向与焊缝长度方向垂直。剪力V在焊缝有效截面上产生沿焊缝长度方向均匀分布的应力。N力产生垂直于焊缝长度方向均匀分布的应力。3种应力状态叠加后,危险点A的受力状态如图3.36所示。

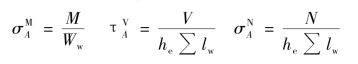
在式(3.10)中代入和,则焊缝计算公式为:

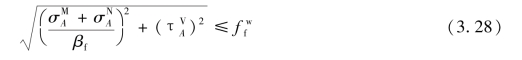
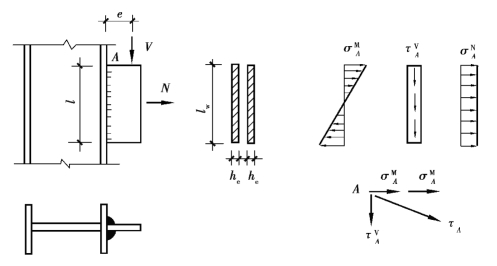
图3.36　受扭、受剪、受轴心力的角焊缝应力

(6)扭矩、剪力、轴力共同作用下角焊缝计算

计算步骤如下:

①求出焊缝有效截面的形心O,如图3.37所示。

②将连接所受外力平移到形心O,得一扭矩T=V(a+e)、剪力V、轴力N。

③计算T,V,N单独作用下危险点A的应力:

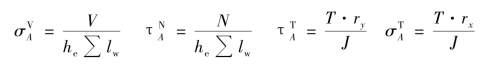
④验算危险点焊缝强度:

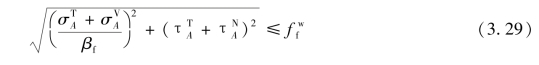
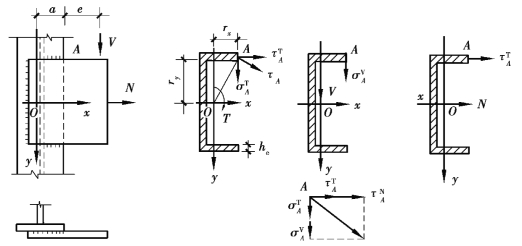
图3.37　受扭、受剪、受轴心力的角焊缝应力

【例3.3】　试确定图3.38所示承受静态轴心力的三面围焊连接的承载力及肢间焊缝长度。已知角钢为2L125×10,与厚度为8mm的节点板连接,其搭接长度为300mm,焊脚尺寸hf=8mm,钢材为Q235B,手工焊,焊条为E43型。

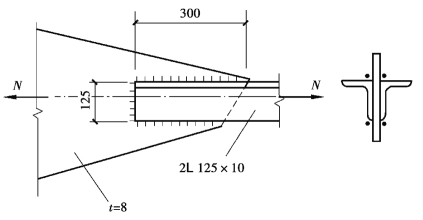
图3.38　例3.3图

【解】　角焊缝强度设计值=160N/mm2。由表3.2知,焊缝内力分配系数为K1=0.70,K2=0.30。正面角焊缝的长度等于相连角钢肢的宽度,即lw3=b=125mm。则正面角焊缝所能承受的内力N3为:由此可计算出肢尖焊缝所要求的实际长度为:

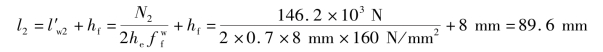
由计算知该连接的承载力N≈943kN,肢尖焊缝长度应为90mm。

【例3.4】　试验算图3.39(a)所示牛腿与钢柱连接角焊缝的强度。钢材为Q235,焊条为E43型,手工焊。荷载设计值N=365kN,偏心距e=350mm,焊脚尺寸hf1=8mm,hf2=6mm。图3.39(b)为焊缝有效截面。

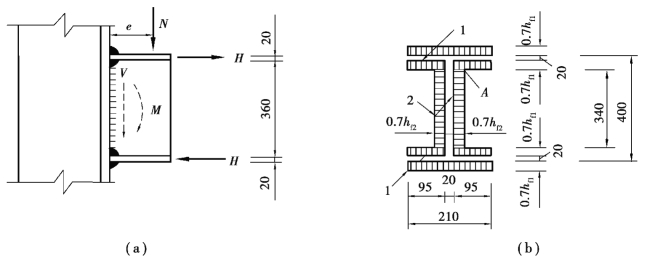
图3.39　工字形牛腿角焊缝计算

【解】　力N在角焊缝形心处引起剪力:V=N=365kN

弯矩:M=N·e=365kN×0.35m=127.8kN·m。

1)考虑腹板焊缝参加传递弯矩的计算方法

根据图3.39(b),全部焊缝有效截面对中和轴的惯性矩为:

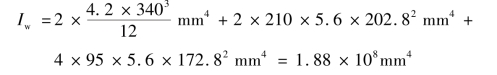
翼缘焊缝的最大应力:

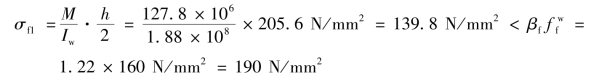
腹板焊缝中设计控制点A由于弯矩M引起的应力:

由于剪力V在腹板焊缝中产生的平均剪应力:

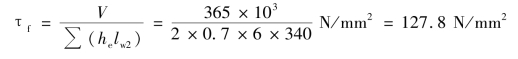
则腹板焊缝的强度(A点为设计控制点)为:

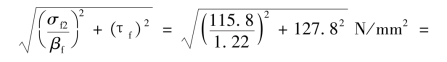
2)按不考虑腹板焊缝传递弯矩的计算方法

翼缘焊缝所承受的水平力:

翼缘焊缝的强度:

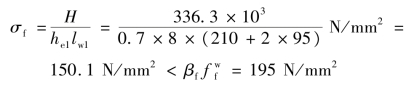
腹板焊缝的强度:

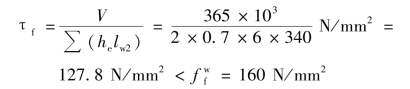
【例3.5】　如图3.40所示,计算支托与柱的连接焊缝。柱翼缘板和支托板厚度t=12mm,材料Q235钢,与柱三面围焊,手工焊。采用E43型焊条,l1=200mm,l2=400mm,作用力F=2×105N,a=200mm,试设计角焊缝。

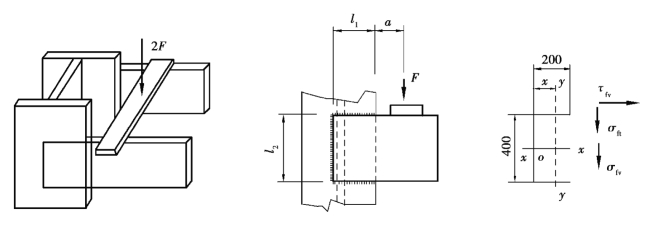
图3.40　例3.5图

【解】　设三边焊缝的焊脚尺寸相同。

取hf=8mm,满足条件:

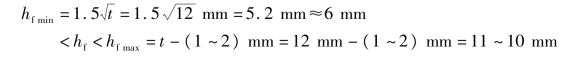
每条焊缝的计算长度均满足大于8hf和小于60hf的要求。

1)几何特性

取hf=8mm,另外考虑弧坑影响lw1=(200-5)mm=195mm。

确定焊缝重心o的坐标

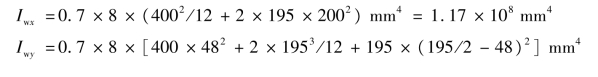
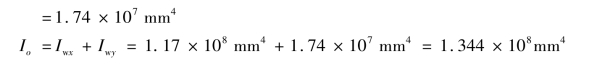
2)内力

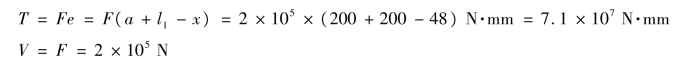
3)焊缝验算

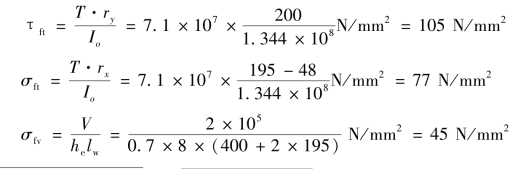
则有,可靠。