定量分析法是指根据现有数据资料，建立在一定数学模型基础上的决策方法。可以使决策过程数学化、模型化，大大提高了科学决策的水平。定量分析难以对许多非程序化的决策课题如涉及政治、社会、心理的决策因素用数学语言加以表达和描述。根据数学模型涉及的决策问题的性质的不同，定量决策方法一般可以分为确定型决策、风险型决策和非确定型决策。

（一）确定型决策

确定型决策的基本特征是：假设事件的各种自然状态是完全肯定而明确的，经过分析计算可以得到各方案的明确结果。确定型决策问题应具备下列条件：具有决策者希望达到的目标；客观条件相对稳定；有两个以上可供选择的方案；各方案执行的结果是明确的。进行确定型决策常用的方法有差量分析法、量本利分析法等。

1.差量分析法　所谓差量是指各个备选方案之间的差别。通过各个备选方案在预期收入、预期成本上的比较，从中选出最优方案的方法，称作差量分析法，也称差别分析法。差量分析主要是通过对比差量收入和差量成本来择优，差量收入是一个备选方案的预期收入与另一个备选方案的预期收入的差异数：差量成本是两个备选方案预期成本的差异数。只要差量收入大于差量成本，那么前一个方案就是较优的；相反，如差量收入小于差量成本，则后一个方案是较优的。

例3－1　某纺织厂可生产两种类型的涤纶面料，生产黑色衬纬涤纶面料1 200m，每米售价1.45元，每米单位变动成本1.1元；如果不生产黑色衬纬涤纶面料而生产涤纶蚊帐面料产品800m，每米售价1.95元，每米单位变动成本1.85元，固定成本不变。试比较分析生产该两种面料哪种最有利？

解：分别计算两种产品生产的差量收入、差量成本与差量损益。

（1）两种产品的差量收入：

1 200×1.45－800×1.95=180（元）

（2）两种产品的差量成本：

1 200×1.1－800×1.85=－160（元）

（3）两种产品的差量损益：

180+160=340（元）

计算分析结果表明，生产黑色衬纬涤纶面料比涤纶蚊帐面料效益要好，可多获利340元。

这种方法一般以企业有同样的生产能力为前提。如果可行方案有两个以上为一组进行比较，最后选择获利最高的方案。

2.量本利分析法　量本利分析法也称为保本分析或盈亏平衡分析。是通过分析企业生产成本、销售利润和产品数量三者之间的关系，掌握盈亏变化规律，指导企业选择获得最大利润的经营方案。量本利分析法常用来进行盈亏平衡分析和经营安全状况分析。

（1）成本与产量的关系。企业从事生产经营活动要消耗大量的人力、物力和财力，它们构成了企业的生产成本。生产成本可划分为固定成本和变动成本。固定成本是指在一定产量范围内，不随产量变动而变动的成本，即使产量为零也要照常支出的费用，如厂房和设备的租金、折旧费、水电费等。从每单位产品的分摊额来看，产量增加，则单位成本降低；产量减少，则单位成本增加。变动成本是指随产量变动而变动的成本，如原料、燃料、直接人工费用等。从单位产品来看，这类成本基本不变。固定成本与变动成本构成产品的总成本。纺织企业在生产经营过程中面临类似的情况，即在一定时期内生产一定数量的产品消耗的成本主要有两部分构成，即固定成本（FC）和变动成本（VC），则总成本（TC）为：

TC=FC+VC

如果产品的单位变动成本为CV，Q表示产品产量（或销量），则VC=CVQ；令P表示产品价格，则销售收入TR=PQ；以π表示利润，则在不考虑税金的情况下有量本利分析的基本等式：

π=TR－TC=PQ－CVQ－FC

（2）盈亏平衡分析和盈亏平衡点的确定。盈亏平衡点又称保本点，是指企业盈亏平衡时的产量（或销量），也就是产品总成本和销售收入相对等时对应的点。即上式π=0时企业的产量。如果以纵轴表示销售收入与总成本，以横轴表示销售量，并在坐标系中画出成本线和收入线，则可得到如图3－3所示的盈亏分析图。由图3－3所示，销售收入TR和总成本线TC的交点，即称之为盈亏平衡点或损益平衡点，此时产量为Q1。在该点上，企业该产品收入与成本正好相等，即处于不亏不盈或损益平衡状态，也称为保本状态。当产量Q＞Q1时，可得到目标利润π，即当π=0，可得到保本点销售量：

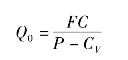
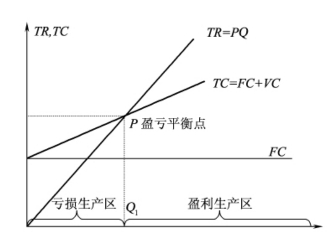
图3－3　盈亏平衡分析图

当π≠0，可得到实现预期利润π的销售量：

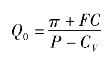
例3－2　某服装厂生产西服，市场售价为1 500元/套，单位变动成本1 100元，固定成本总额为5 000 000元，目标利润为10 000 000元，试求保本点和实现目标利润的销售量各为多少？

解：将有关数据代入式（3－1）和式（3－2），可得到盈亏平衡点销售量：

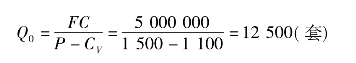
实现目标利润的销售量：

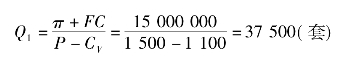
（3）量本利分析法的应用。量本利分析法在纺织企业决策中的应用范围非常广，主要体现在以下几个方面。

①作为判断生产方案的重要依据，通过对比企业当前产量与盈亏平衡点产量，可知生产的盈亏状况，如果现实产量低于盈亏平衡点的产量，则方案不可取；反之，方案可取。

②判断企业经营状况。经营状况的好坏主要通过经营安全率L来衡量

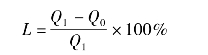
其中Q1－Q0为安全余额，即实际销售量与盈亏平衡点销量的差额，其经济意义为安全余额越大，说明企业的盈利水平越高；反之，越低，其具体的参考数值见表3－1。

表3－1　企业经营安全状态

（二）风险型决策

风险型决策又称随机决策，是指客观存在着不以人的意志为转移的两种以上的自然状态。虽然未来事件可能出现的自然状态是不确定的，但各种自然状态可能发生的概率却是可以预测的，在这种条件下所作的决策即为风险型决策。

风险型决策一般要具备以下几个条件。

①决策者有一个明确的目标。

②存在着两个以上的行动方案，和不以决策者的个人意志为转移的两种以上的客观自然状态。

③各种自然状态发生的概率是可以估计和预测的。

④不同方案在各种自然状态下的损益值可以计算。这里所说的自然状态的概率，一般是从调查研究和历史资料中进行统计分析求得，即客观概率；或者来自决策者主观经验的判断，即主观概率。

风险型决策所依据的标准主要是期望值标准。期望值就是在不同自然状态下决策者所期望达到的数值。风险型决策方法主要有决策表法、决策树法等。

1.决策表法　决策表法又称期望值法或决策矩阵法。这种方法，首先，利用有关资料确定事件发生的概率；其次，利用矩阵表计算并表现出各个行动方案与各种自然状态相结合下的条件收益或条件损失；再次，利用上述概率和条件损益算出期望值并进行比较；最后，选择可以获得最大收益或最小损失的方案为最优方案。

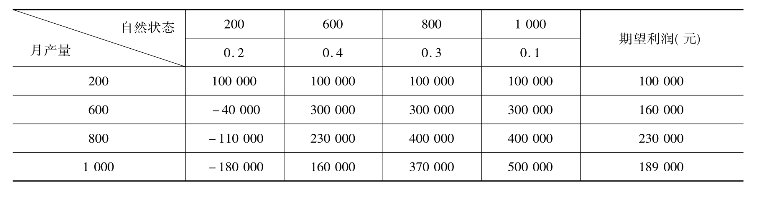
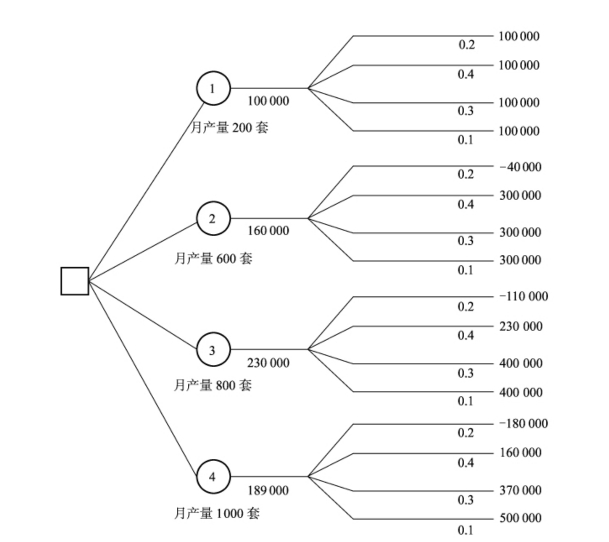
例3－3　某服装厂拟确定西服的月产量决策。根据以往数据，过去每年同期月产量分别为200套、600套、800套、1 000套：概率一次为0.2，0.4，0.3，0.1。而每套西服的出厂成本为300元/套，市场售价800元/套，而当月产出西服如不能及时出厂要付出库存成本每套50元，试问该服装厂的月最佳产量为多少？

解：（1）根据以往同期西服销售资料的分析，可确定今年同期产品生产量的自然状态，并计算出各种状态下的概率，绘制决策收益表（表3－2）。

表3－2　新产品决策收益表

（2）根据以往的销售情况，经过分析，拟定出新产品销售的可行方案。

（3）计算各种行动方案的期望损益值Ei。

EMVi=∑πiPi

式中：EMVi——第i个方案的期望效益值；

πi——不同概率下的收益值；

Pi——事件出现的概率。则有：EMV1=100 000×（0.2+0.4+0.3+0.1）=100 000（元）

EMV2=－40 000×0.2+300 000×（0.4+0.3+0.1）=160 000（元）

EMV3=－110 000×0.2+230 000×0.4+400 000×（0.3+0.1）=230 000（元）

EMV4=－180 000×0.2+160 000×0.4+400 000×0.3+500 000×0.1=189 000（元）

结果以第三种方案为最佳，即月产量为800套时企业受益最大。即根据收益矩阵决策者应该选择当月产量为800套。

2.决策树法　在风险型决策中，除了可以用决策收益表法进行决策外，还可以用决策树进行决策。所不同的是决策树既可以解决单阶段的决策问题，还可以解决决策收益表无法表达的多阶段序列决策问题，具有思路清晰、阶段明确等优点。决策树法是利用树枝图形列出决策方法、自然状态、自然状态概率及其损益，然后计算各个方案的期望损益值，进行比较选择。决策树的基本原理也是以决策收益计算为依据，进行选优决策。所不同的是，决策树是一种图解方式，对分析复杂的问题较为实用。

（1）决策树的构成。决策树有决策点、方案枝、状态节点、概率枝和期望值五个要素构成。决策树的决策点为决策的出发点，由决策点引出若干决策枝，每一决策枝代表一个方案，方案枝的末端为状态节点，状态节点又引出概率枝，每一概率枝代表着一种自然状态，概率末端为期望值。整个形状像“树”型，因而称之为决策树。决策树的一般结构如图3－4所示。

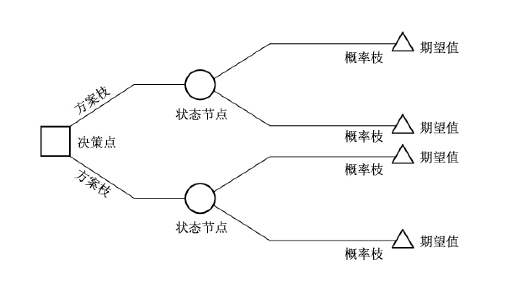
图3－4　决策树一般结构示意图

（2）决策步骤。

①绘制决策树。决策树图是对某个决策问题未来可能发生的情况与方案的可能结果的表示。因此，画决策树图的过程就是拟订各种方案的过程，也是进行状态分析和估算方案可能结果的过程。所以，要对决策问题的发展动向步步深入地进行分析，并按决策树的结构规范由左向右来依次画出决策树图。

②计算期望值。将各自然状态的收益值或损失值分别乘以概率枝上的概率，并将这些值相加，求出状态节点和决策点的收益期望值或损失期望值。期望值的计算方法，从决策树的右边向左边逐步进行。一般把计算结果标示在图中。

③剪枝选定方案。根据不同方案期望值的大小，从右向左（逆推法）进行修枝优选。舍去期望收益值小的方案，留下期望收益值最大的方案。最后便可得出最优方案，并写出结论。

决策树法的主要特点是使用了决策树图，因而整个决策分析过程具有直观、简要、清晰等优点。决策树分析既可用于单阶段的决策，也可用于多阶段的复杂决策。

a.单阶段决策。是指在整个决策中只决策一次，就能选择出决策的行动方案的过程。单阶段决策计算简单，方法简便易行。

以上题为例，运用决策树法，求解如下：

第一步，依据题意，画出决策树图（图3－5）。

第二步，从右到左，计算各节点期望值。

节点①期望值：

100 000×（0.2+0.4+0.3+0.1）=10（万元）

(www.daowen.com)

图3－5　不同月产量时的决策树图

节点②期望值：

－40 000×0.2+300 000（0.4+0.3+0.1）=16（万元）

节点③期望值：

－110 000×0.2+230 000×0.4+400 000×（0.3+0.1）=23（万元）

节点④期望值：

－180 000×0.2+160 000×0.4+400 000×0.3+500 000×0.1=18.9（万元）

第三步，比较节点①、②、③、④，剪去节点①、②、④，决策结果即为月产量应该定在800套。

b.多阶段决策。如果决策问题较复杂，在决策中一次决策不能解决问题需要进行多次决策才能确定决策的行动方案，称为多阶段决策。

例3－4　某涤纶面料厂拟投资扩大生产规模，根据市场预测分析，明年产品的销路有两种可能：销路好和销路一般，各种情况出现的概率为0.7和0.3。涤纶面料厂有两种方案可以选择：新建生产线；改进生产线。若今年没上新生产线，到明年市场需求旺盛，企业还可以采取两种方案：紧急安装新生产线；外包。

各种方案的收益值在表3－3中给出。

表3－3　多阶段决策收益表

解：

（1）依据题意，画出决策树图（图3－6）。

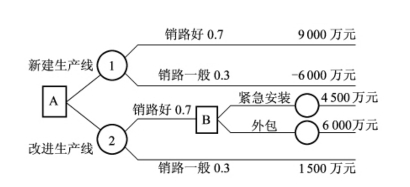
图3－6　不同投资模式下的决策树图

（2）从右到左，先找决策点B的方案值。

决策点B的值：

Max（4 500，6 000）=6 000（万元）

状态节点①净收益值：

9 000×0.7+（－6 000）×0.3=4 500（万元）

状态节点②净收益值：

6 000×0.7+1 500×0.3=4 650（万元）

（3）比较决策点A，状态节点①的收益值为4 500万元，状态节点②的收益值为4 650万元，以最大净收益值作为评价标准，该涤纶面料厂应该选择改进生产线的方案。

最后得到的方案是，今年采用改进生产线的方式；如果明年销路好，则采用外包的方案，如果销路一般，则用原来的生产能力。

（三）非确定型决策

非确定型决策是指在决策所面临的自然状态难以确定而且各种自然状态发生的概率也无法预测的条件下所做出的决策。由于自然状态下决策结果的不可预知，因此具有较大的风险性和主观随意性。在非确定型决策中，由于方案实施后的结果无法做出估计。因此，决策在很大程度上取决于决策者的主观判断，不同的决策者对同一问题的决策结果也可能是完全不一样。非确定型决策常遵循以下几种思考原则。

1.悲观原则　持这种决策原则的决策者，都是对未来事件的结果估计比较保守的。他们力求从不利的情况下寻求较好的方案，即从坏处着眼向好处努力。先分别找出每个方案在各种自然状态下的最小收益值，再将各方案的最小收益值相比较，选出最大数值的方案作为决策方案。即从最坏的情况出发，选择最有利的方案，又称保守型决策。

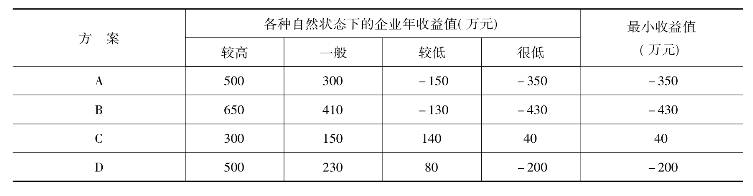
例3－5　某纺织企业拟生产一种新产品，由于缺乏资料，企业对这种产品的市场需求量只能大致估计为四种情况：较高，一般，较低，很低。对这四种自然状态发生的概率无法预测。生产这种新产品企业考虑有四个可行方案，各方案的损益情况见表3－4。

表3－4　各方案最小收益情况

解：

（1）从每个方案中选出最小值{－350，－430，40，－200}。

（2）从各方案的最小值中选择最大值所对应的方案Max{－350，－430，40，－200}=40（万元）。

（3）最优方案应选择C方案。

2.乐观原则　持这种决策原则的决策者，都是对未来前景比较乐观，并有较大成功把握的，愿意承担一定风险去争取最大的收益。

这种方法与悲观原则正好相反，也称为最大值收益法。仍以上例为例（表3－5），选择过程是：首先从每个方案中选择一个最大收益值；然后从这些最大收益值中选择一个最大值，这个最大值所对应的方案就为最优方案。即表中所示的B方案。

表3－5　各方案最大收益情况

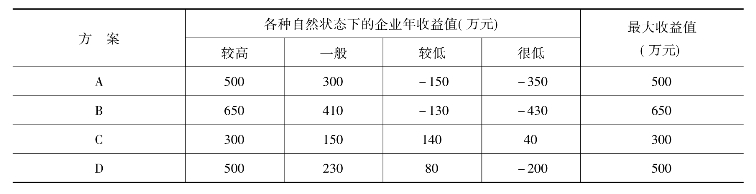
这种方法期待今后出现的情况是最有利的，往往过分乐观，容易引起冒进或出现极不合理的现象。

3.折中原则　这种决策原则的指导思想是，稳中求发展，既不过于乐观也不过于悲观，寻求一个较稳定的方案。

这种方法是，首先考虑每一个方案的最大收益值和最小收益值，然后应用一个系数对最大收益值和最小收益值进行折中调整，计算出它们的调整收益值，最后以最大的调整收益值EMV所对应的方案作为最优方案。

EMV=α×最大收益值+（1－α）×最小收益值

式中：α——乐观系数，α=0～1。

α通常由决策者根据对获得最大收益值的可能性的估计，自主选定。不难看出，当α=1时，这种方法就变成乐观原则决策方法；当α=0时，这种方法就变成悲观原则决策方法。

若α=0.6，则（1－α）=0.4，其各种方案相应收益为：

EMV（A）=0.6×500+0.4×（－350）=160（万元）

EMV（B）=0.6×650+0.4×（－430）=218（万元）

EMV（C）=0.6×300+0.4×40=196（万元）

EMV（D）=0.6×500+0.4×（－200）=160（万元）

比较计算结果，B方案的收益值最大，为最佳方案。

4.最小后悔值法　这种决策方法也叫最小机会损失法。所谓机会损失就是在各种自然状态下决策者选定方案的收益与最大收益之间的差额。机会损失也称为后悔值，每个方案在各种自然状态中都有一个最大的机会损失。利用这种决策方法是把各方案的最大机会损失选出来进行比较，哪个方案的最大机会损失最小，哪个方案就是最优的方案。机会损失的计算和分析有如下步骤。

（1）找出每种自然状态下的最大收益值。

（2）分别求出每种自然状态下各个方案的机会损失（机会损失值=最大收益值－方案收益值）

（3）找出对应于各种自然状态的最大收益值，在表3－6中用*标出。

（4）将对应于每种自然状态的各项收益值从相应的最大值中减去，求出后悔值（表3－7）。

表3－6　各方案收益情况

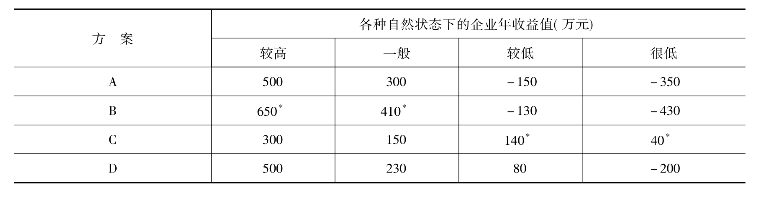
表3－7　各方案后悔值求法

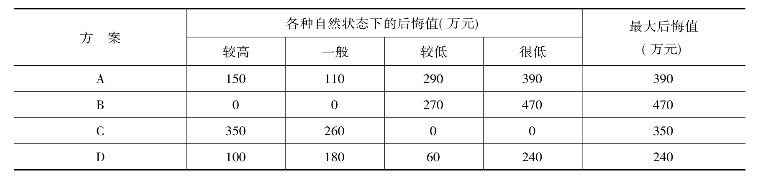
再次，找出各个方案的最大后悔值{390，470，350，240}。

（5）从各个方案的最大后悔值中再选择最小后悔值，其所对应的方案Min{390，470，350，240}=240（万元）为最优方案。D方案是最优的决策方案。

对于上述四种决策方法，在理论上还不能证明哪一种是最合理的。因此，在实际经营决策中，要因事、因人而异。

技能实训

以小组为单位，选定纺织企业，在对企业进行调查的基础上，了解定性和定量决策方法在企业中的运用。

案例综合分析

某纺织厂是一个生产涤纶面料的老厂，过去该厂曾有骄人的业绩。但随着人员老化、长久的粗放式管理，企业中的问题也随处可见，从日常的点滴到生产现场、人员素质等方面都存在着或多或少的问题。

有一位厂长经常发现车间饮水处的水龙头没有关紧，滴滴答答地漏水，为此组织员工开会，要求禁止这一行为，并制定了管理制度。但事过一段时间仍有此现象发生，气得厂长直埋怨员工素质差。

该厂生产车间的设备较多，并且有些较为老化，螺丝的松动是设备维修人员有时最感头痛的事。因为，如果设备在运转中主要的螺丝产生松动，小则造成设备带病运行，大则产生质量和设备事故。但是，又不能每天用手或工具去检查每一个螺丝，这给管理带来了很大的不便。

车间的机器由于长久不清洗，油渍、缠飞花现象比较严重，抓棉机的打手处经常存在挂花和卫生死角，此类现象也同样出现在梳棉、并条、粗纱、细纱等设备上。另外，员工在搬运原料纱和棉卷的过程中，由于检查工作不细致，经常导致原料和回花混入异性纤维，配棉和混棉场所也存在类似问题。棉卷搬运路线的不确定经常使工作现场混乱。

在成品车间同样存在着成品不分的现象，生产现场成品、半成品的合格品区域、不合格品区域划分不清，使现场人员不得不多花大量的时间再去分拣，从而大大降低了工作效率。

车间安全事故时有发生，由于工作的疏忽，使员工在平时的工作中，对有些机器设备如清花、梳棉等的危险部位视而不见。另外，车间消防设备不健全，在车间外地上也存在着烟灰现象。

·讨论题：

如何用定性的决策方法解决上述企业存在的诸多问题？