有限元方法的核心思想就是“离散化”，即将一个包含无限自由度的连续物体，通过网格划分，变成一个只有有限自由度的离散体（图1-5）。有限元方法的基本思路如下。

（1）离散化（网格划分）离散化也就是所说的单元网格划分，将结构人为地划分成有限个子域（这些子域被称为单元），假定单元之间通过有限个点相互连接（这些连接点被称为节点或节点）。

在进行离散化时，作以下假设（图1-6）：①物体由有限大小单元（Finite ele-ment）组成；②单元间通过节点连接、节点传递力；③载荷等效为节点载荷；④节点位移为求解未知量——位移法。

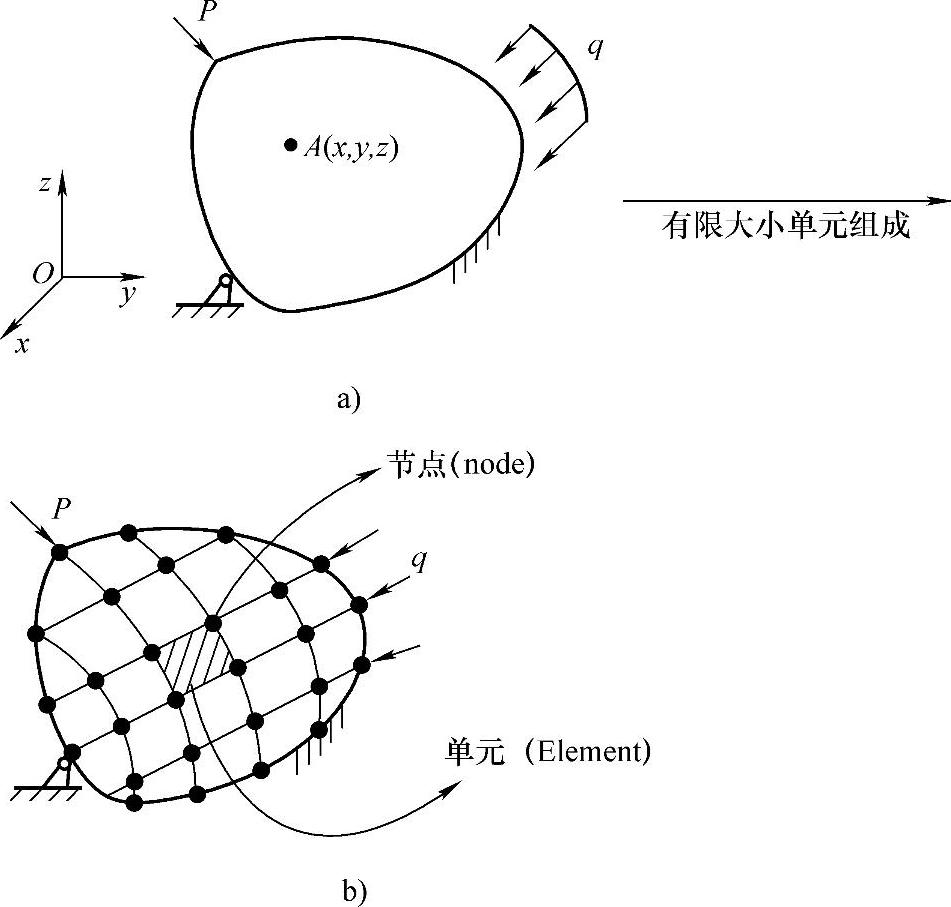
图1-5 有限元网格划分

a）连续体（无限自由度） b）离散体（有限自由度）

通常把三维实体划分成四面体或六面体单元的网格，平面问题划分成三角形或四边形单元的网格。

（2）单元分析 在离散化后，分析任意单元e的受力与变形关系（图1-7）。

1）假设节点位移和节点力：

δ_if_i（i，j，m，p）

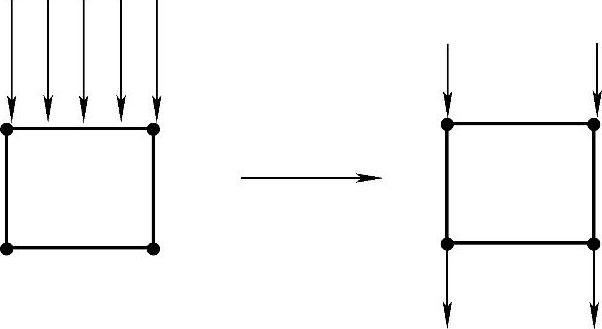
图1-6 离散化

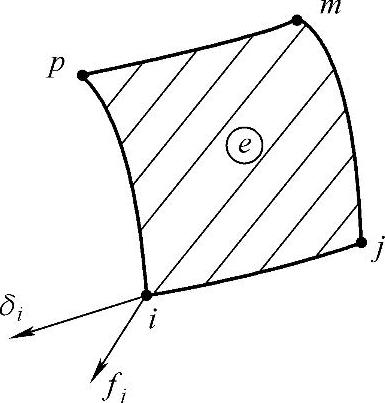
图1-7 分析单元e的受力与变形关系

2）写成矢量的形式：

单元节点位移矢量：

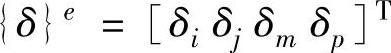(www.daowen.com)

节点力矢量：

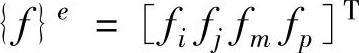
3）建立节点力{f}^e与节点位移{δ}^e之间的关系（力与变形关系）：

{f}^e=[k]^e{δ}^e，[k]^e为单元刚度矩阵

（可以类比弹簧刚度方程（受力与变形关系）f=kx，k刚度系数。）

单元刚度矩阵与单元内部的材料、变形分布有关。

（3）整体分析 将所有的单元刚度方程整合，形成整体系统刚度方程为

{P}=[K]{δ}

式中，{P}为整体系统节点载荷矢量；[K]为整体系统刚度矩阵；{δ}为整体系统节点位移矢量。

（4）求解 求解刚度方程，可以得到节点位移、单元内部位移、单元内部应变，从而得到单元内部的应力为

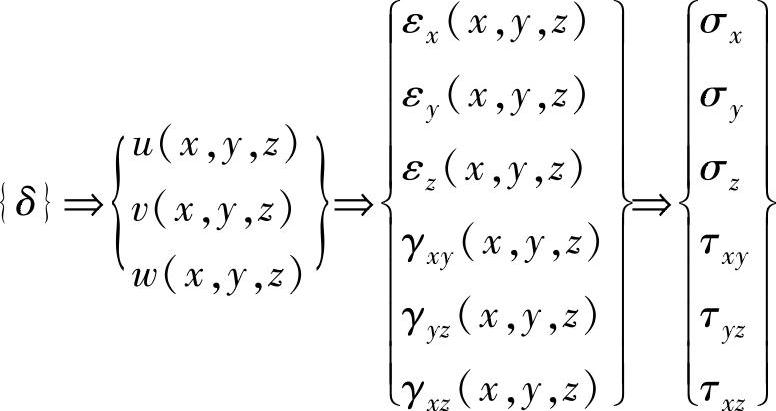
综上所述，可以看出有限元方法的基本特点：

1）“一分一合”。分：连续体（无限自由度）—离散体（有限自由度）—单元分析。合：整体分析、求解。

2）有限元方法能处理复杂的结构形状、边界条件及载荷。

3）有限元方法是一种近似的数值方法。