GNSS-RTK（Real Time Kinematics）测量模式要求至少有两台同时工作的GNSS接收机，由基准站通过数据链实时将载波观测量及基站坐标信息一同传送给流动站。流动站接收GNSS卫星的载波相位与来自基准站的载波相位，并组成相位差分观测值进行实时处理，实时给出厘米级的定位结果。

流动站接收机利用基准站和流动站的基线向量（ΔX，ΔY，ΔZ）加上基准站坐标得到流动站每个点的WGS-84坐标，通过坐标转换得出流动站每个点的坐标（x，y，h）。

根据以上所述基准站和流动站的运作，用户可携带流动站系统在测区又快又准地进行定位测量和放样测设工作。由于即时计算点位坐标，用户对系统的工作可实时监察。基准站传输原始数据时并不限制接收对象，所以适配某一基准站工作的流动站数量不受限制。

载波相位差分是将基准站采集的载波相位发送给流动站进行求差解算坐标。将基准站上观测的载波相位通过数据链传送到流动站，流动站静止不动观测若干历元后进行计算，求解其相位模糊度，这一过程称为初始化。

求差法，即单差，双差和三差三种数学模型，已广泛应用于静态测量中。载波相位求差法的基本思想是：基准站T0不再计算测相伪距修正数　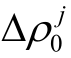，而是将其观测的载波相位观测值由数据链实时发送给用户接收机，然后由用户机进行载波相位求差，再解算出用户的位置。

在基准站T0和流动站Ti上同时在t1和t2历元上观测了两颗卫星（Sj，Sk），基准站的载波相位观测值由数据链实时传送给流动站。这样，用户共获得了8个观测值，即

式中　δt——仪器和卫星钟差；

ρ——仪器至GNSS卫星的真距离；

，ΔT——电离层和对流层延迟影响。

将两台接收机在同一历元观测同一卫星的载波相位观测值相减，得到4个单差方程：

从上式中看出，单差方程中已消去了卫星钟差。将两台接收机同时观测两颗卫星的载波相位观测值求差，即同一历元的单差相减，得到两个双差方程，如下式：(www.daowen.com)

由上式看出，此双差方程中已消去了接收机的钟差。双差方程右端的初始整周模糊度通过初始化进行解算。

静态测量数据处理的主要任务是求解基线向量。因此它的计算程序是：

利用三差法求解出近似的基线长度，再利用浮动双差法求解出相位模糊度和基线向量。将求得的相位模糊度凑整后，进行固定双差的计算，最后求解出精密的基线向量。

但在动态应用中，我们要求的不是基线向量，而是流动站所在的实时位置。因此它的计算程序如下：

（1）在初始化阶段，静态观测若干历元。历元数目的多少取决于流动站到基准站的距离。在数据处理中，重复静态观测的程序，求出相应位置模糊度，并确认此相应位置模糊度正确无误。

（2）将求出的相应位置模糊度代入双差方程中。由于基准站的位置坐标是精确测定的已知值，两颗卫星的位置坐标可由星历参数计算出来，故双差方程中的未知数只有用户在协议地球系中的位置坐标（Xi，Yi，Zi）。此时，只要观测3颗卫星就可进行求解。这样，在实际作业中，观测4～6颗星，就可实时准确地求解（Xi，Yi，Zi）。

将基准站的地心坐标（Xb，Yb，Zb）输出，就可求得流动站的地心坐标：

将当地坐标系与地心坐标的转换参数输出，就可得到当地坐标系的直角坐标：

上述所讨论的单基准站差分GNSS系统结构和算法简单，技术上较为成熟，主要适用于小范围的差分定位工作。对于较大范围的区域，则应用局部区域差分技术，对于一国或几个国家范围的广大区域，应用广域差分技术。