GNSS基线解算就是利用GNSS观测值，通过数据处理，得到测站的坐标或测站间的基线向量值。

在布设GNSS网时，首先需对构成GNSS网的基线进行观测，并利用所采集到的GNSS数据进行数据处理，通过基线解算，获得具有同步观测数据的测站间的基线向量。为了确定GNSS网中各个点在某一特定坐标系统下的绝对坐标，需要提供位置基准、方位基准和尺度基准，而一条GNSS基线向量只含有在WGS-84下的水平方位、垂直方位和尺度信息，通过多条GNSS基线向量可以提供GNSS网的方位基准和尺度基准。

由于GNSS基线向量中不含有确定网中各点绝对坐标的位置基准信息，因此，仅凭GNSS基线向量所提供的基准信息，是无法确定出网中各点的绝对坐标的。而我们布设GNSS网的主要目的是确定网中各个点在某一特定局部坐标系下的坐标，这就需要从外部引入位置基准，这个外部基准通常是通过一个以上的起算点来提供的。GNSS网平差可利用所引入的起算数据来计算出网中各点的坐标。当然，GNSS网的平差，除了可以解求出待定点的坐标以外，还可以发现和剔除GNSS基线向量观测值和地面观测中的粗差，消除由于各种类型的误差而引起的矛盾，并评定观测成果的精度。

一、GNSS网平差的分类

GNSS网平差的分类方法有多种，根据平差所进行的坐标空间，可将GNSS网平差分为三维平差和二维平差；根据平差所采用的观测值和起算数据的数量和类型，可将平差分为无约束平差、约束平差和联合平差等。

1.三维平差和二维平差

（1）三维平差。

所谓三维平差，是指平差在三维空间坐标系中进行，观测值为三维空间中的观测值，解算出的结果为点的三维空间坐标的平差方法。GNSS网的三维平差，一般在三维空间直角坐标系或三维空间大地坐标系下进行。

（2）二维平差。

所谓二维平差，是指平差在二维平面坐标系下进行，观测值为二维观测值，解算出的结果为点的二维平面坐标的平差方法。

2.无约束平差、约束平差和联合平差

（1）无约束平差。

GNSS网的无约束平差是指在平差时不引入会造成GNSS网产生由非观测量所引起的变形的外部起算数据。常见的GNSS网的无约束平差，一般为在平差时没有起算数据或没有多余的起算数据。

（2）约束平差。

GNSS网的约束平差指的是平差时所采用的观测值完全是GNSS观测值（即GNSS基线向量），而且在平差时引入了使GNSS网产生由非观测量所引起的变形的外部起算数据。

（3）联合平差。

GNSS网的联合平差指的是平差时所采用的观测值除了GNSS观测值以外，还采用了地面常规观测值，这些地面常规观测值包括边长、方向、角度等。

二、GNSS网平差原理

1.三维无约束平差

（1）定义。

所谓GNSS网的三维无约束平差，是指平差在WGS-84三维空间直角坐标系下进行，平差时不引入使GNSS网产生由非观测量所引起的变形的外部约束条件的平差方法。具体地说，就是在进行平差时，所采用的起算条件不超过三个。对于GNSS网来说，在进行三维平差时，其必要的起算条件的数量为三个，这三个起算条件既可以是一个起算点的三维坐标向量，也可以是其他的起算条件。

（2）作用。

GNSS网的三维无约束平差有以下三个主要作用：

①评定GNSS网的内部符合精度，发现和剔除GNSS观测值中可能存在的粗差。

由于三维无约束平差的结果完全取决于GNSS网的布设方法和GNSS观测值的质量，因此，三维无约束平差的结果就完全反映了GNSS网本身质量的好坏，如果平差结果质量不好，则说明GNSS网的布设或GNSS观测值的质量有问题；反之，则说明GNSS网的布设或GNSS观测值的质量没有问题。

②得到GNSS网中各个点在WGS-84坐标系下经过了平差处理的三维空间直角坐标。

在进行GNSS网的三维无约束平差时，如果指定网中某点准确的WGS-84坐标作为起算点，则最后可得到经过了平差处理的在WGS-84坐标系下GNSS网中各个点的坐标。

③为将来可能进行的高程拟合，提供经过了平差处理的大地高数据。

用GNSS水准替代常规水准测量获取各点的正高或正常高是目前GNSS应用中一个较新的领域，现在一般采用的是利用公共点进行高程拟合的方法。在进行高程拟合之前，必须获得经平差的大地高数据，三维无约束平差可以提供这些数据。

（3）原理。

在GNSS网三维无约束平差中所采用的观测值为基线向量，即GNSS基线的起点到终点的坐标差，因此，对于每一条基线向量，都可以列出如下的一组观测方程：

与此相对应的方差-协方差阵、协因数阵和权阵分别为

式中，σ0为先验的单位权中误差。

平差所用的观测方程就是通过上面的方法列出的，但为了使平差进行下去，还必须引入位置基准。引入位置基准的方法一般有两种：第一种是以GNSS网中一个点的WGS-84坐标作为起算的位置基准，即可有一个基准方程：

第二种是采用秩亏自由网基准，引入下面的基准方程：

根据上面的观测方程和基准方程，按照最小二乘原理进行平差解算，得到平差结果。

其中，n为组成GNSS网的基线数，p为网中的基线向量数。

协因数阵：Q=（BTPB+GGT）-1。

（4）单位权方差的检验。

平差后单位权方差的估值　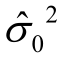应与平差前先验的单位权方差　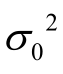一致，判断它们是否一致可以采用　χ2-检验。

原假设H0：

备选假设H1：

其中

若则H0成立；反之，则H1成立。(www.daowen.com)

2.三维联合平差

GNSS网的三维联合平差一般是在某一个地方坐标系下进行的，平差所采用的观测量除了GNSS基线向量外，有可能还引入了常规的地面观测值，这些常规的地面观测值包括边长观测值、角度观测值、方向观测值等；平差所采用的起算数据一般为地面点的三维大地坐标，除此之外，有时还加入了已知边长和已知方位等作为起算数据。

3.二维联合平差

二维联合平差与三维联合平差很相似，不同的是二维联合平差一般在一个平面坐标系下进行。与三维联合平差一样的是，平差所采用的观测量除了GNSS基线向量外，有可能还引入了常规的地面观测值，这些常规的地面观测值包括边长观测值、角度观测值、方向观测值等；平差所采用的起算数据一般为地面点的二维平面坐标，除此之外，有时还加入了已知边长和已知方位等作为起算数据。

三、GNSS网平差的过程

在使用数据处理软件进行GNSS网平差时，需要按以下几个步骤进行：

（1）提取基线向量，构建GNSS基线向量网。

（2）三维无约束平差。

（3）约束平差/联合平差。

（4）质量分析与控制。

1.提取基线向量，构建GNSS基线向量网

要进行GNSS网平差，首先必须提取基线向量，构建GNSS基线向量网。提取基线向量时需要遵循以下几项原则：

（1）必须选取相互独立的基线，若选取不相互独立的基线，则平差结果会与真实的情况不相符合。

（2）所选取的基线应构成闭合的几何图形。

（3）选取质量好的基线向量。基线质量的好坏，可以依据RMS、RDOP、RATIO、同步环闭合差、异步环闭合差和重复基线较差来判定。

（4）选取能构成边数较少的异步环的基线向量。

（5）选取边长较短的基线向量。

2.三维无约束平差

在构成了GNSS基线向量网后，需要进行GNSS网的三维无约束平差。进行无约束平差主要达到以下几个目的：

（1）根据无约束平差的结果，判别所构成的GNSS网中是否有粗差基线，如发现含有粗差的基线，需要进行相应的处理，必须使得最后用于构网的所有基线向量均满足质量要求。

（2）调整各基线向量观测值的权，使得它们相互匹配。

3.约束平差/联合平差

在进行完三维无约束平差后，需要进行约束平差或联合平差，平差可根据需要在三维空间或二维空间中进行。

约束平差的具体步骤如下：

（1）指定进行平差的基准和坐标系统。

（2）指定起算数据。

（3）检验约束条件的质量。

（4）进行平差解算。

4.质量分析与控制

在这一步，进行GNSS网质量的评定，在评定时可以采用下面的指标：

（1）基线向量的改正数。

根据基线向量改正数的大小，可以判断出基线向量中是否含有粗差。具体判定依据是，若，则认为基线向量中不含有粗差；反之，则含有粗差。

（2）相邻点的中误差和相对中误差。

若在进行质量评定时，发现有质量问题，需要根据具体情况进行处理，如果发现构成GNSS网的基线中含有粗差，则需要采取删除含有粗差的基线、重新对含有粗差的基线进行解算或重测含有粗差的基线等方法加以解决；如果发现个别起算数据有质量问题，则应该放弃有质量问题的起算数据。

5.GNSS网平差中起算数据的检验

在进行GNSS网的约束平差或联合平差时，对起算数据进行质量检验是很必要的。由于在GNSS网平差中所用的起算数据一般为点的坐标，因此，在这里将主要介绍对起算点坐标的检验。

（1）方差检验法。

在进行三维无约束平差时，要进行方差估计，调整观测值的权，直至验后的单位权方差与先验的单位权方差相容。在进行约束平差时，以三维无约束平差所得到的验后单位权方差作为先验的单位权方差，逐个加入起算数据进行平差解算，同时检验验后的单位权方差与先验的单位权方差之间的相容性，当在加入了某一起算数据后发现它们不一致，则说明该起算数据可能存在质量问题。

（2）附合路线法。

附合路线法是从一个起算点通过一条由GNSS基线向量组成的GNSS导线推算另一个起算点的坐标，将此坐标与已知值比较，根据它们差异的大小来判断起算点的质量。为准确地判断起算点质量的好坏，一般需要采用多条附合路线。

（3）检查点法。

在进行平差解算时，不将所有起算点坐标固定，而是保留一个点作为检查点，平差后比较该点坐标的平差值和已知值，根据它们差异的大小来判断起算点质量的好坏。为准确地判断起算点质量的好坏，一般需要轮换地将各个起算点分别作为检查点。