1.GNSS网的精度设计

精度是用来衡量网的坐标参数估值受观测偶然误差影响程度的指标。网的精度设计是根据偶然误差的传播规律，按照一定的精度设计方法，分析网中各未知点平差后预期能达到的精度。精度一般常用网点坐标的方差-协方差阵来表示，也可用误差椭圆来描述，或者用方位、距离和角度的标准差来定义。

GNSS网的精度一般用网中点之间的距离误差来表示。然而，对于大多数工程控制网来讲，仅用点位之间距离的精度来表示网的精度是不够的，还需要提供GNSS网中各点点位精度和网中的平均点位精度来表示网的精度。即可用网点坐标的方差-协方差阵构成描述精度的纯量精度标准和准则矩阵来实现。纯量精度标准是选择不同的描述全网总精度的变量，构成不同的纯量精度标准，并用其来建立优化设计的精度目标函数。准则矩阵是由网中点的坐标方差-协方差阵构成的具有理想结构的矩阵，它代表了网的最佳精度分布，具有更细致描述网的精度结构的控制标准。但是，对于GNSS测量，正如前述，其精度与网的点位坐标无关，与观测时间无明显相关性（整周模糊度一旦被确定以后），GNSS网平差的法方程只与点间的基线数目有关，且基线向量的三个坐标分量之间又是相关的，因此，很难从数学的角度和实际应用出发建立使未知数的协因数阵逼近理想状态的准则矩阵。所以，目前较为可行的方法是给出坐标协因数阵的某种纯量精度标准函数。设GNSS网有误差方程：

式中，V、l分别为观测向量及其改正数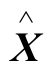；为坐标未知参数向量；P为观测向量的权阵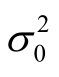；为先验单位权方差（也称先验方差因子，在设计阶段取　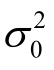＝1）。

由最小二乘原理可得参数的估值及其协因数阵为

优化设计中常用的纯量精度标准，根据其由　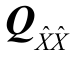构成的函数不同而又有四种不同的最优纯量精度标准函数。

（1）A最优性标准：

式中，Trace表示矩阵的迹；λ1，λ2，…，λt为　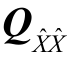的非零特征值。

（2）B最优性标准：

式中，Det表示行列式的值。

（3）C最优性标准：

式中，λmax为　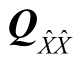的最大特征值。

（4）D最优性标准：

式中，λmin为　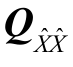的最小特征值。

以上四个最优纯量精度标准函数中，B、C、D三个标准需要计算行列式和特征值，而对于高阶矩阵，这些计算都是比较困难的，因此，在实际中应用较少，一般多用于理论研究。相反，A最优性标准函数求的是　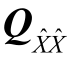的迹，计算方便，避免了特征值的计算，因此在实际中应用较多。在实际应用中还可根据工程对网的具体要求，将A最优性标准变形为

式中，C为平均点位误差要求限值。

2.GNSS网精度设计实例

对GNSS测量进行网形设计，必须考虑精度要求。GNSS网精度设计可按下列步骤进行：

（1）根据布网目的，进行图上选点，并到野外踏勘选点，以保证所选点满足测量任务要求和野外观测应具备的条件，用图解方法在图上获得各观测点位的概略坐标。(www.daowen.com)

（2）根据将要使用的接收机台数N，选取（N-1）条独立基线设计网的观测图形，并选定网中可能追加施测的基线。

（3）根据GNSS控制网测量的精度要求，采用解析-模拟方法，依据精度设计模型，计算将要施测的GNSS网可达到的各项精度指标值。

（4）逐步增减网中独立观测基线，直至精度指标值达到GNSS网所预期的精度指标，并获得最终网形及施测方案。

GNSS网的精度设计可依据程序进行，图2.1.8是GNSS网精度设计的程序流程框图。

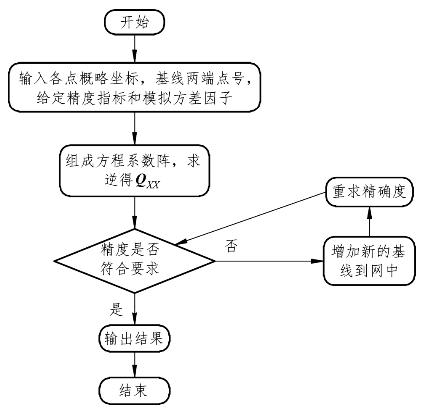
图2.1.8　GNSS网的精度设计程序流程

例如：对一个由8点组成的GNSS模拟网，进行网的精度设计。该网8个点的概略大地坐标由图上量取并列于表2.1.8，点位及网形如图2.1.9所示。

在图2.1.9中，独立基线为1—2，1—3，1—4，2—4，2—6，3—4，3—7，5—6，5—7，5—8，6—8，7—8，共计12条GNSS基线。

表2.1.8　GNSS模拟网坐标值

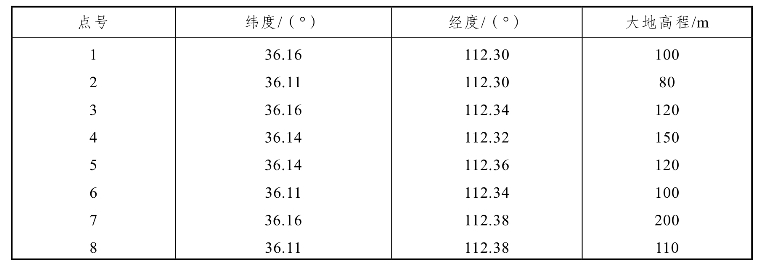
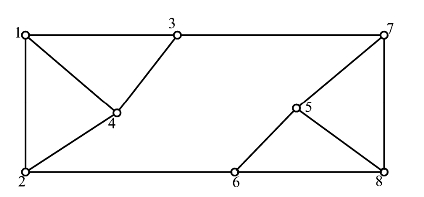
图2.1.9　GNSS模拟网

假定单位权方差　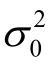=1，以1号点作为基准点，设计后的平均点位误差要求为2.2 cm（即C＝2.2 cm）。

假定GNSS基线长、方位和高差见表2.1.9。

表2.1.9　GNSS基线长、方差和高差的精度

根据图2.1.9独立基线构成的GNSS网形结构，由式（2.1.7）可求出网的平均谐因数值，进而求出网的平均点位误差为

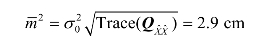
可见，没有达到设计的精度要求。因此，需要在网中加测基线，并重新计算协因数及平均点位误差：

由计算结果可以看出，增加3—5、4—5、4—6（图2.1.10中的虚线边）共三条基线后，就达到了设计的精度要求。因此，最终设计图形及需要观测的独立基线如图2.1.10所示。

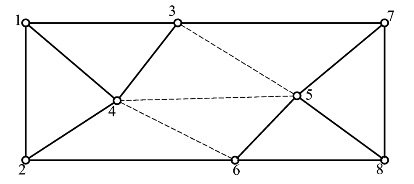
图2.1.10　增加基线后的GNSS模拟网

在实际工作中，精度设计的试算过程都是利用计算机进行的。