与GPS卫星有关的误差主要包括卫星星历误差、卫星钟的钟误差和相对论效应。

一、卫星星历误差

卫星作为高空运行的动态已知点，其瞬时的位置是由卫星星历提供的。卫星星历的误差实质就是卫星位置的误差，即由卫星星历计算得到的卫星的空间位置与卫星实际位置之差。在GPS测量中，卫星是作为已知点的，因此，卫星星历误差是一种起算数据误差，在一个观测时段里，对观测量的影响主要呈现系统误差特性。卫星星历误差的大小主要取决于卫星跟踪系统的质量，如卫星跟踪站的数量及空间分布、观测值的数量及精度、轨道计算时所选用的轨道模型及定轨软件的完善程度等。另外，卫星星历误差与星历的预报间隔也有直接关系。卫星星历误差将严重影响单点定位的精度，在精密相对定位中也是一个重要的误差源。

1.星历误差来源

卫星星历的数据来源有预报星历（广播星历）和后处理星历（精密星历）两类。

（1）预报星历。它是根据美国GPS控制中心跟踪站的观测数据进行外推，通过GPS卫星发播的一种预报星历，是卫星电文中所携带的主要信息。由于我们还不能充分了解作用在卫星上的各种摄动因素的大小及变化规律，所以预报数据中存在着较大的误差。

当前从卫星电文中解译出来的星历参数共17个，每小时更换一次。由这17个星历参数确定的卫星位置精度为20～40 m，有时可达80 m，随着定轨技术和摄动力模型的改善，其定位精度可以提高到5～10 m。广播星历对导航用户与实时定位用户具有十分重要的作用。

（2）精密星历。又称为后处理星历，属于实测星历。它是根据实测资料进行拟合处理而直接得出的星历。它需要在一些已知精确位置的点上跟踪卫星来计算观测瞬间的卫星真实位置，从而获得准确可靠的精密星历。这种星历要在观测后1～2个星期才能得到，这对导航和动态定位无任何意义，但是在静态精密定位中具有重要作用。

精密星历通常有偿地为所需用户服务。目前的GPS 精密星历主要有两种：由美国国防制图局（DMA）生产的精密星历以及由国际GPS服务（IGS）生产的精密星历。前者的星历精度约为2 m；后者的星历精度则优于30 cm。IGS是一个非军方的国际协作组织，其开放度也较高。

此外，GPS卫星是高轨卫星，区域性的跟踪网也能获得很高的定轨精度。所以许多国家和组织都在建立自己的GPS卫星跟踪网开展独立的定轨工作。

2.星历误差对定位的影响

在GPS 定位中，一般都把由卫星星历所给出的卫星在空间的位置视为已知值，此时星历误差将成为一种起算数据误差。这种误差对单点定位和相对定位有不同的影响。下面分别予以介绍：

（1）对单点定位的影响。

对于单点定位，星历误差的径向分量作为等价测距误差进入平差计算，配赋到星站坐标和接收机钟差改正数中去，具体配赋方式则与卫星的几何图形有关。

卫星星历误差在卫星间可以看成是独立的，但同一卫星在一段时间内的星历误差具有很强的相关性，呈现系统性的偏差。即使连续观测较长的时间（1～2 h），也难以消除卫星星历误差对单点定位的影响。一般说来，卫星单点定位误差的量级大体上与卫星星历误差的量级相同。利用广播星历，卫星星历误差对测站坐标的影响一般可达数米、数十米甚至上百米，因此广播星历通常只能满足导航和低精度单点定位的需要。进行厘米级精度的精密单点定位时必须使用高精度的精密星历。

（2）对相对定位的影响。

利用两站的同步观测资料进行相对定位时，由于星历误差对两站的影响具有很强的相关性，所以在求坐标差时，共同的影响可自行消去，从而获得高精度的相对坐标。因此，星历误差对相对定位的影响远小于对单点定位的影响。

星历误差对相对定位的影响通常采用下式来进行估计：

式中　ρ——卫星到观测站的几何距离；

dρ——卫星的星历误差；

D——基线向量长度；

dD——由卫星星历误差引起的基线误差。

式中系数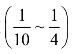的具体取值取决于基线向量的位置与方向、观测时段的长短、观测的卫星数量及其几何分布等因素。

目前，广播星历的精度为5～10 m，星历误差对相对定位的影响为10-7级；即使是在实施SA政策广播星历的精度被人为地降低至100 m时，仍可达到0.5～ 1.2 ppm（1 ppm=10-6），可满足一般控制测量和工程测量的要求。但随着基线距离增加，卫星星历误差引起的基线误差将不断增大。因此，对于长距离、高精度的GPS测量，需要采用精密星历。(www.daowen.com)

3.削弱或消除卫星星历误差的措施

（1）采用精密星历。在高精度的应用领域中， 可使用精密星历。IGS的成立为我们提供了方便。

建立自己独立的卫星跟踪网。建立自己的卫星跟踪网，独立测定卫星轨道参数，可以获得很高的定位精度。这对确保导航和实时定位的可靠性和精度有很重要的意义，尤其在非常时期，可以不受美国政策有意降低调制在C/A码上的卫星星历精度的影响。独立的卫星跟踪网，不仅可以向进行事后处理的用户提供精密星历，而且还可以向进行导航和实时定位的用户提供经精密星历外推得到的较为准确的预报星历。我国已经在北京、上海、武汉、西安、拉萨、乌鲁木齐建立GPS跟踪站。通过跟踪站的监测，精密星历的精度可能达到0.25 m，从而满足1 000 km基线相对的精度达到10-8的要求。

（2）采用相对定位模式。也称为同步观测值求差，这一方法是利用在两个或多个观测站上，对同一卫星的同步观测值求差，因为星历误差对相距不太远的两个测站的影响基本相同，所以对于确定两个测站之间的相对位置，可以减弱卫星星历误差的影响。

采用相对定位模式时，即使基线长度达56 km，广播星历误差的影响仍保持在1 cm以内。采用这种方法布设的GPS网具有很高的相对精度。该法简单，效果显著，因而被广泛使用。

（3）轨道松弛法。所谓轨道松弛法，就是在平差模型中把卫星星历给出的卫星轨道视为初始值，将其改正数作为未知数，通过平差求得测站位置及轨道改正数。这种方法不适用于范围较小的测区，此外数据处理相当复杂，工作量大为增加，不宜在作业单位普遍推广，只适用于无法获取精密星历而采取补救措施的情况。

二、卫星钟的钟误差

1.卫星钟钟误差的来源

卫星钟采用的是GPS时，它是由主控站按照美国海军天文台（USNO）的协调世界时（UTC）进行调整的。GPS时与UTC在1980年1月6日零时对准，不随闰秒增加，时间是连续的，随着时间的积累，两者之间的差别将表现秒的整倍数；如有需要，可由主控站对卫星钟的运行状态进行调整，不过这种遥控调整仍然满足不了定位所需的精度。此外，尽管GPS卫星均设有高精度的原子钟（铷钟和铯钟），但它们与理想的GPS时之间仍存在着难以避免的频率偏差或频率漂移，也包含钟的随机误差。这些偏差总量在1 ms以内，由此引起的等效距离可达300 km，显然无法满足定位精度的要求。在GPS测量中，卫星作为高空观测目标，其位置在不断变化，必须有严格的瞬间时刻，卫星位置才有实际意义。另外，GPS测量就是通过接收和处理GPS信号实现定位的，必须准确测定信号传播时间，才能准确测定观测站至卫星的距离。所以时钟误差是一个重要误差源之一。

2.削弱或消除卫星钟钟误差的措施

在GPS测量中一般可采用下列方法解决钟误差：

（1）采用钟差改正法。GPS定位系统通过地面监控站对卫星的监测，测试卫星钟的偏差。卫星钟的偏差可用二阶多项式的形式加以表示，改正参数通过卫星导航电文发送给用户。应用二项式模拟卫星钟的误差只能保证卫星钟与标准GPS时间同步在20 ns之内。由此引起的等效偏差不会超过6 m。

（2）观测量差分法。卫星钟差或经改正后的残差，在相对定位中可通过差分法得到消除，即在接收机间求一次差分的方法来进一步消除。

（3）通过其他渠道获取精确的卫星钟差值。

在某些应用中，例如利用载波相位观测值进行精密单点定位（Precise Point Positioning，PPP）时，观测值的精度很高，对定位结果的精度要求也很高，自然对卫星钟差也会提出很高的要求。此时根据卫星导航电文中给出的钟参数求得的卫星钟差已不能满足要求，故需通过其他渠道来获取精确的卫星钟差值，如通过国际GPS服务IGS来获取精确的卫星钟差。由于下列原因，IGS能给出精度更高的卫星钟差和卫星星历：

①与GPS地面监控部分相比，IGS的定轨站数量更多，地理分布更好。

②IGS定轨时用的是载波相位观测值（辅之以测码伪距观测值），而广播星历是根据测码伪距导得的。

③IGS给出的最终卫星星历和卫星钟差均为实测的结果，而GPS卫星导航电文中给出的都是预报值。

④IGS所采用的定轨模型及数据处理软件更为严密、完善。目前IGS综合星历中给出的卫星钟差的精度可达0.1 ns。

三、相对论效应

GPS 测量中相对论效应是由于卫星钟和接收机钟所处的状态（运动速度和重力位）不同而引起的卫星钟和接收机钟之间产生相对钟误差的现象。相对论效应主要取决于卫星的运动速度和重力位，并且是以卫星钟的误差这一形式表现的。GPS卫星在高20 200 km的轨道上运行，卫星钟受相对论效应的影响，其频率与地面静止钟相比，将发生频率偏移，这是精密定位中必须顾及的一种误差影响因素。

由于相对论效应的影响，使一台钟放到卫星上去后的频率比在地面时增加。解决相对论效应的最简单的办法就是在制造卫星钟的时候预先把频率降低　。因此，当降低频率以后的卫星钟进入轨道后受到相对论效应的影响，频率正好变为标准频率10.23 MHz。

上述结论是在卫星轨道为圆形、运动为匀速（轨道半径Rs＝26 560 km，运动速度v＝3 874 m/s，光速度c＝299 792 458 m/s，地球半径Rm＝6 378 km）的情况下推导出来的。但实际上GPS卫星的轨道是一个椭圆，卫星的运行速度也随着时间发生变化，故此时将相对论效应视为常数显然不符合实情，而应是时间的函数，即按上述降频的方法改正以后仍存在残差。当GPS卫星轨道椭圆的偏心率等于0.01，GPS卫星的偏近点角等于90°时，相对论效应的影响达到最大值，它对GPS时间的影响最大可达22.897 ns，相当于6.864 m的站星距离，在精密定位中是不容忽视的。