一、绝对定位原理

绝对定位是以地球质心为参考点，用户用一台GPS接收机，一般使用GPS信号中的C/A码或P码作为测距信号，测得用户至GPS卫星的距离，从而解算出待定点在协议地球坐标系中的绝对位置。由于定位只需要一台接收机，具有速度快、灵活方便且无多值性问题等优点，故广泛应用于低精度的测量和导航中。绝对定位包括静态绝对定位和动态绝对定位。

二、静态绝对定位

静态绝对定位是在接收机处于静止状态下，确定测站的三维地心坐标。所依据的观测量是根据码相关测距原理测定的卫星至测站间的伪距，从而解算出其三维地心坐标。

1.伪距法绝对定位解算

根据任务二中学习过的伪距观测方程（1.4.7），其中不仅含有一个测站Ti的三个未知的三维地心坐标　δXi、δYi、δZi，还有一个钟差未知数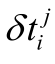，因此需要同步观测四颗卫星，才能组成四个伪距方程，从而解算出测站Ti的三维地心坐标，如图1.4.2所示。

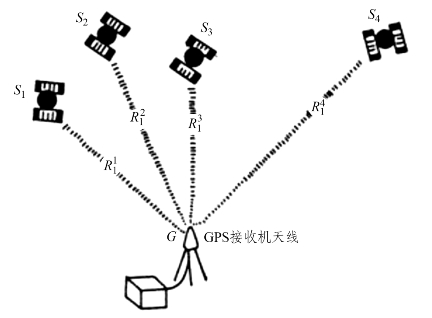
图1.4.2　静态绝对定位示意图

假如现在电离层和对流层延迟等效距离误差已经通过适当的模型推出，即目前已经知道了，则可将公式（1.4.10）进行变形，可令

则伪距方程可以改写成

式中，j＝1，2，3，4。将方程化成矩阵的形式如下：

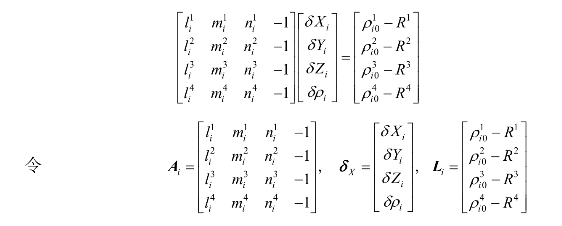
则可将其简化为

由伪距法绝对定位解可以表示为

当同步观测的卫星多于4颗时，则应可用最小二乘法求解，其组成误差方程式为

按最小二乘法解算得到

这一定位方法一般用于测定工作中的单点定位，以较精确地确定观测站在WGS-84坐标系中的绝对坐标。

其中反映定位精度的权系数矩阵为

参数向量各个分量的中误差：

式中，0σ为伪距测量的中误差；iiq为矩阵　XQ主对角线的相应元素。

如果观测的时间较长，接收机钟差的变化是不能忽略的。这时可将钟差表示成多项式的形式，把多项式的系数作为未知数在平差中求解。也可以对不同观测历元引入独立的钟差参数，在平差中求解。

2.载波相位观测值静态绝对定位

在应用载波相位观测值进行静态绝对定位时，需要在观测值中加入电离层、对流层等各项改正，探测出周跳并修复，以提高定位的精度。整周未知数解算后，不再为整数的可将其调整为整数，解算出测站坐标称为固定解，否则称为实数解。

三、动态绝对定位

GPS动态绝对定位原理与静态绝对定位原理相似，只是在GPS动态绝对定位中，需要确定运动载体上的接收机天线相位中心的瞬间位置。由于接收机天线处于运动的状态，故其天线相位中心坐标值是一个不断变化的量，因此确定每一瞬间坐标的观测方程只有较少的多余观测。其主要方法有测码伪距和测相伪距的动态绝对定位法。一般选用C/A码作为观测量，因此其定位精度较低，一般为十几米到几十米，所以此种方法只适用于精度要求不高的车辆运动载体的导航。

1.测码伪距动态绝对定位法

如果仅观测四颗卫星，无多余观测量，解算是唯一的。但是如果同步观测的卫星数多于四颗，则需要用最小二乘法平差求解。

如果历元t中观测站至所测卫星之间的伪距已经经过了卫星时钟差改正则有

取，则测码伪距观测方程可写为

为了确定观测站坐标和接收机钟差，至少需要四个伪距观测量。假设任一历元t，由观测值Ti同步观测四颗卫星分别为j＝1，2，3，4，则有四个伪距方程：

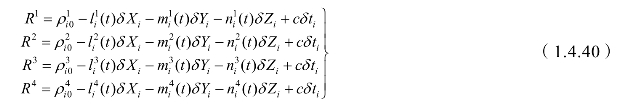
当卫星数多于4颗的时候，可列出方程组，按照最小二乘法求解出点位的三维地心坐标。求得四颗卫星的坐标如下：

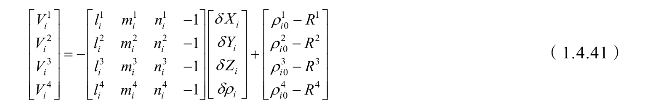
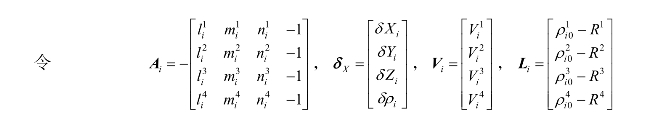(www.daowen.com)

用矩阵的符号表示为

用最小二乘法可得

由此可求得待定点的坐标

（Xi0，Yi0，Zi0）为待定点的初始坐标，在动态定位中，一般可将前一时刻的点位坐标作为当前时刻点位的初始坐标，因此，保证第一个点位坐标的精确，才能为后续点位的解算提供初始坐标值。由于该点的初始值难以精确地获得，所以需要多次迭代方可获得满意的结果。

2.测相伪距动态绝对定位法

载波相位观测方程比测距码观测方程多了一个整周未知数，所以利用测相伪距进行动态定位一般无法实时求解，想要获得动态实时解的关键在于能否预先或者在运动中可靠地确定载波相位观测值的整周未知数。而且载体在运动的过程中，要始终保持对所测卫星的连续跟踪，目前在技术上有一定的困难，同时加之目前动态解算整周未知数的方法，在应用上也有局限性，所以在实时动态定位中目前主要采用的是测码伪距的方法。

四、绝对定位精度评价

利用GPS进行绝对定位时，定位精度主要取决于两个因素：所测卫星在空间的几何分布，通常称为卫星分布的几何图形；另外一个因素是观测量的精度。

1.绝对定位精度的评价

当以测码伪距为观测量，进行动态绝对定位时，其权系数阵可表示为　，可一般的表示为

其中，元素ijq表达了全部解的精度及其相关信息，是评价定位结果的依据。上述权系数阵一般是在空间直角坐标系中给出的，而实际为了估算观测站的位置精度，常采用其在大地坐标系中的表达式。假设在大地坐标系中的相应坐标权系数阵为

根据方程与协方差传播定律：

式中，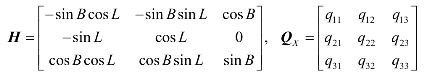

为了评价GPS定位结果，一般采用精度因子DOP（dilution of precision）的概念，并以此作为衡量卫星空间几何分布对定位精度影响的标准。由权系数阵（1.4.42）中主对角线元素定义精度因子DOP，则相应的精度表示为

式中，σ0为伪距测量的中误差。在实践中，根据不同要求，可选用不同的精度评价模型和相应的精度因子。通常有：

（1）平面位置精度因子HDOP（Horizontal DOP）：

相应的中误差为

（2）高程精度因子VDOP（Vertical DOP）：

相应的中误差为

（3）空间三维位置精度因子PDOP（Position DOP）：

相应的中误差为

（4）接收机钟差精度因子TDOP（Time DOP）：

相应的中误差为

（5）几何精度因子GDOP（Geometric DOP），是描述空间位置误差和时间误差综合影响的精度因子：

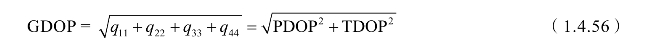
相应的中误差为

GPS绝对定位的误差与精度因子DOP的大小成正比，在伪距观测精度σ0确定的情况下，使精度因子的值尽可能小，是提高定位精度的一个重要途径。由于精度因子与所测卫星的空间分布有关，因此也称观测卫星的图形强度因子。因为卫星的运动及选择卫星的不同，所测卫星在空间分布的几何图形是变化的，那么精度因子的数值也是变化的。

假设观测站与四颗卫星构成的六面体体积为V，经研究表明，精度因子GDOP与该六面体体积V的倒数成正比，即

一般来说，六面体的体积越大，所测卫星在空间的分布范围也越大，GDOP值越小；反之，卫星分布范围越小，GDOP值越大。根据理论分析得到，在观测站到四颗卫星的观测方向中，当任意两方向之间的夹角接近109.5°时，其六面体体积最大。但是在实际观测中，还存在大气折射的影响，所以实际工作中的选址和评价观测卫星分布图形应该是一颗卫星位于天顶，其余三颗卫星相距120°时，所构成的六面体的体积接近最大。