伪距法定位是由GPS接收机在某一时刻测出4颗以上的GPS卫星的伪距得到已知点的卫星位置，采用距离交会的方法求定接收机天线所在点的三维坐标。伪距测量是由GPS卫星发射的测距码信号到达GPS接收机的传播时间乘以光速所得到的距离。由于卫星钟、接收时钟和信号经过大气层的延迟，实际测量出的距离与卫星接收到的几何距离有一定的偏差，因此一般把这样量测出的距离称为伪距（即不是真实的距离）。用C/A码进行测量的伪距称为C/A码伪距，用P码测量的伪距称为P码伪距。

测距码伪距测量的原理是接收机接收到卫星传送来的测距码后，接收机的振荡器立即产生与卫星传来的测距码码形结构完全相同的伪随机噪声码，两组码结构相同，但是相位不同，即码没有对齐，通过延时器使码对齐（在实际的工作中，由于误差的存在，两者只能无限的接近对齐），对齐所用的时间即为测距码在空间传播的时间，进而乘以光速得到伪距。C/A码和P码这两种测距码的伪距观测误差最大分别是2.9 m和0.29 m。虽然定位的精度不高，但是却有速度快等优点，故仍然是一种常用的方法。

一、测码伪距

测码伪距测量是通过测量地面接收机接收到GPS卫星的信息中的测距码信号所用的时间，从而计算出地面接收机到卫星的距离。其公式为

式中，Δt为信号传播的时间；c为光速。

要准确测定测站与卫星之间的距离就必须使卫星钟与用户接收机时钟保持同步，但实际中却会存在卫星钟与接收机钟误差以及无线电信号经过电离层和对流层有延迟误差，这会导致实际测出的伪距与真实的伪距有一定的差值。

用tj（GPS）表示第j颗卫星发出信号瞬间的GPS标准时间，tj是相应卫星钟钟面时刻，δtj表示卫星钟钟面与相对GPS标准时的差；ti（GPS）表示接收机在第i个测站上收到卫星信号瞬间的GPS时间，ti是相应的接收机钟面时刻，δti表示接收机钟面相对于GPS标准时间的差。即有下面的关系：

在不考虑大气层对信号的影响的前提下，可以推算出卫星到达接收站之间的伪距：

为了方便表示，用ρ 表示卫星到接收站之间的几何距离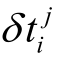，表示接收机时钟和卫星时钟的相对误差。则（1.4.4）可以简化为

再用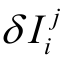表示电离层引起的距离偏差，用　δTij表示此刻对流层引起的距离偏差，这个是随用户高程及气象的不同而变化的，所以，最后的伪距方程可以写成：

上式表示的是卫星在轨道位置和用户位置的函数。如果已知第j颗卫星，则测得的伪距可以写成：

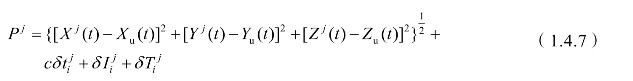
其中，Xj（t）、Yj（t）、Zj（t）是t时刻卫星j的三维地心坐标，Xu（t）、Yu（t）、Zu（t）是测站的三维地心坐标。显然这个方程是非线性的，计算起来费时且麻烦。因此需要把它化成便于计算机解算的形式，即对其进行线性化。设　Xi、Yi、Zi为测站三维地心坐标的近似值，δXi、δYi、δZi为测站坐标的改正值，且导航电文所提供的卫星瞬时坐标为固定值，则有

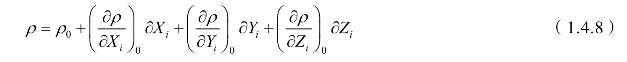
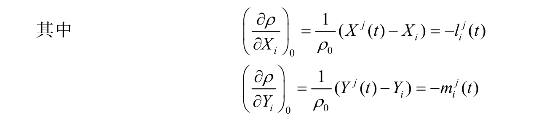
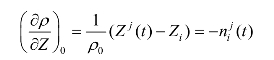
所以其几何距离线性化表达式为

而为站星几何距离的近似值，带入式（1.4.6）得到线性化的伪距观测方程：

二、测相伪距

测相伪距与测码伪距之间的差异在于伪距的获取方式不同，测码伪距是由码相位观测到的伪距，而测相伪距是由载波相位观测到的伪距。载波相位观测量是接收机和卫星位置的函数，得到了它们之间的关系才能从中解算出接收机的位置。

设在GPS标准时刻ti（GPS）、卫星时钟钟面时刻ti的卫星Sj发射的载波信号的相位为φj（tj），在接收机钟面时间ti收到信号后产生的基准信号相位为φi（ti）。应该顾及载波相位差的整周数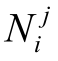，此时载波相位的观测量为

对于卫星钟和接收机钟，其振荡频率一般稳定良好，所以其信号的相位与频率的关系可表示为

其中，f为信号频率；Δt为微小时间间隔；φ以2π为单位。

由于卫星钟与接收机钟的标准时间存在着差异，因此有

tj（GPS）和ti（GPS）表示与钟面tj、ti相应的标准GPS时间，δtj、δti表示接收机与卫星钟的钟差改正数，则

假设，jf为j卫星发射的载波频率，1f为接收机本振荡产生的固定参考，则有

所以相位观测量又可以写为

考虑到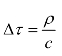，同时电离层和对流层对信号传播延迟Δτ的影响，最终Δτ可以用下式表示：

式中，c为电磁波传播速度；ρ为卫星到接收机之间的几何距离。所以载波相位测量的观测方程可写成：

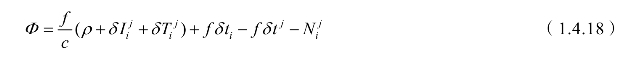(www.daowen.com)

将公式（1.4.15）两边同时乘以，即可以得到

三、整周未知数的确定、周跳探测与恢复

1.整周未知数N0确定

当以载波相位进行精确定位时，在连续跟踪某颗卫星j的所有载波相位的观测值中，均含有相同的整周未知数N0，准确确定N0是高精度定位的关键。因此，确定N0是载波相位测量中一项重要的工作。常用的方法主要有以下几种：

（1）整周未知数的平差待定参数法——经典方法。

①整数解（固定解）。

整周未知数从理论上讲应该是一个整数，但是由于误差的存在，平差求得的整周未知数往往不是一个整数，而是一个实数。所以一般短基线定位时采用这种方法。具体步骤是：首先，根据卫星位置和修复周跳后的观测值进行平差计算，得到基线向量和整周未知数；然后，将整周未知数取为整数，如果此刻整周未知数的整数候选值不止一个，则应将所有的候选值构成不同的组合，并重新进行平差计算；最后，取使基线解方差最小的那组整数作为整周未知数。

②实数解（浮动解）。

当基线较长时，误差的相关性降低，如卫星星历、大气折射等误差的影响将消除的不够全面，所以不论是基线向量还是整周未知数，精确度均较低。因此对于20 km以上的长基线通常不再考虑整周未知数的整数性质，而是直接将实数解作为整周未知数的解。由实数整周未知数获得的基线解也称为浮动解。

（2）伪距法。

伪距法是在进行载波相位测量的同时又进行了伪距测量，将伪距观测值减去载波相位的实际观测值后可以得到λ·N0。但是由于伪距测量的精度比较低，使用多次观测λ·N0的平均值才能勉强得到正确的整周未知数。

（3）三差法（多普勒法）。

根据载波相位的观测值的线性组合可知，在连续跟踪载波相位观测值中均含有相同的整周未知数N0，所以在相邻两个观测历元的载波相位求差中直接将该未知的参数消去，从而解算出坐标参数，这种方法称为三差法。同时由于三差法利用了连续跟踪卫星的两个历元间的相位差等于多普勒积分值这一特性，所以此方法又称为多普勒法。同时又由于卫星的两个历元间观测值之差会受到接收机时钟和卫星钟的误差影响，所以精度不高。

（4）交换接收天线法。

观测之前，在待定点附近5～10 m处选择一个天线交换点，将两台接收机天线分别安置在这两点，同步观测若干个历元后，相互交换天线，并继续观测若干个历元，最后再把这两个天线恢复到原来的位置。此时以这两点之间的基线向量为起始基线向量，利用天线交换前后的同步观测量，求解基线向量，进而确定整周未知数。

2.周跳的探测与恢复

GPS载波相位测量，只能测量载波滞后相位1周以内的小数部分，而载波滞后的整周数N0是当接收机捕获卫星信号后，只要跟踪不中断，接收机便会给出在跟踪期间载波相位整数周的变化。但在实际中，卫星信号如果被障碍物暂时遮挡、外界干扰因素影响或者由于仪器线路的瞬间故障，经常引起卫星跟踪信号的暂时中断，从而导致接收机整周计数中断，这种现象称为整周跳变，简称周跳。当接收机恢复对该卫星的跟踪后，所测相位的小数部分不受跟踪中断的影响，仍然是连续的，但是整周计数由于失去了在连锁期间载波相位变化的整周数，不再连续，使其后的相位观测值，均含有同样的整周误差。因此周跳对于测量成果的精度有明显的影响，需在数据预处理阶段探测出周跳发生的位置，并对其进行修正。下面介绍几种常用的探测和修复周跳的方法。

（1）屏幕扫描法。

如果卫星的相位观测值出现了周跳，则相位观测值的变化率将不再连续。凡曲线出现不规则变化时，就意味着相应的观测值中出现了整周跳变。此方法主要应用在早期GPS相位测量数据处理中，主要靠作业人员在计算机屏幕前依据变化率的图像进行逐段检查，观察其变化率是否连续。但此法也存在费时且只能发现大周跳的缺点。

（2）高次差或多项式拟合法。

此方法是利用在没有周跳的情况下，载波相位的变化随卫星接收机平缓而有规律的变化而变化，如果有周跳存在将破坏这一规律。如果在相邻的两个观测值间依次求差且求得观测值的一次差，这一次差的变化就小得多，在此基础上再求二次差、三次差、四次差，其变化就小得更多了。一般而言，当相位观测值之间求4～5次差时，距离变化对整周数的影响已趋近于零，这时候的差值主要是接收机振荡器的随机误差引起的，具有随机的特性（见表1.4.1）。

表1.4.1　相位观测值高次差

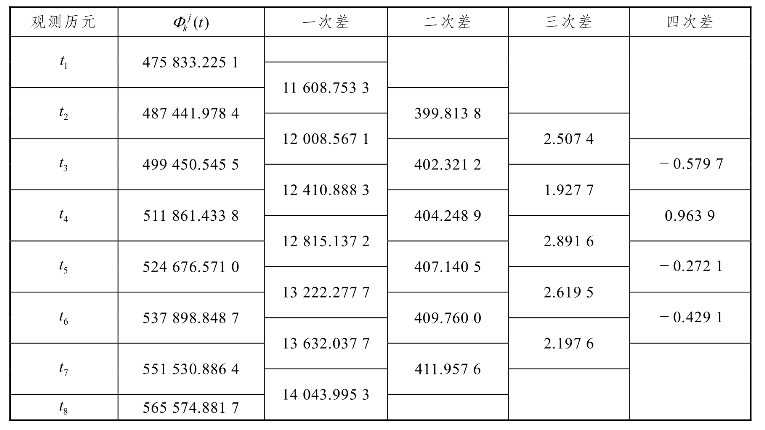
如果在观测过程中发生了周跳，首先这个随机性规律会被破坏，其次高次差还会出现“误差放大”的现象，此时就能发现有周跳现象的时段。如表1.4.2所示，历元ts发生了100周的周跳使第四次差产生异常。但此方法一般难以探测出只有几周的小周跳。

表1.4.2　含有周跳的相位观测值高次差

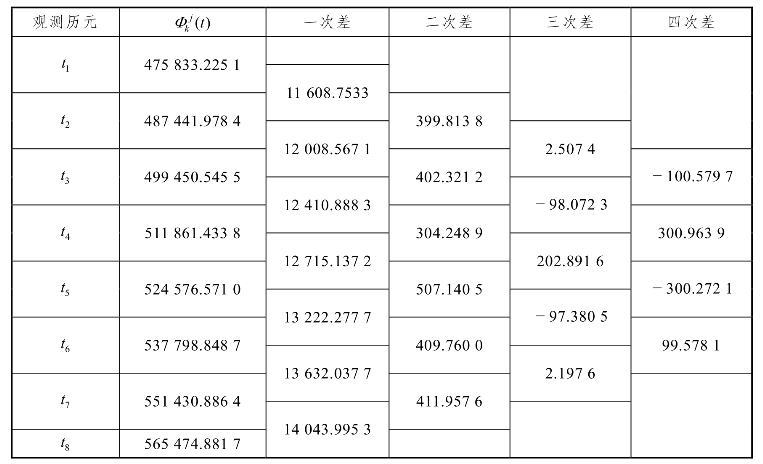
如果用多项式拟合也可以发现周跳，可以根据若干个相位的观测值拟合一个n阶多项式，根据此多项式来预估下一个观测值并与实际值比较，从而发现周跳并修复。

（3）卫星间求差法。

由于每颗卫星的载波相位观测值受到的接收机振荡器的随机误差的影响相同，所以在卫星间求差就可以消除由接收机振荡器的随机误差引起的周跳误差。

某历元时刻接收机k对卫星m的相位观测量：

某历元时刻接收机k对卫星n的相位观测量：

则　，不存在整周数的影响。

（4）双频观测值修复周跳。

双频GPS接收机有两个频率的载波，则双频接收机的两个载波频率的相位观测量为

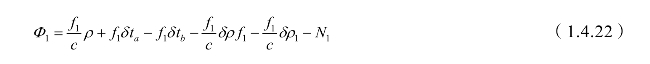
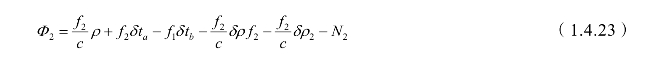
同时考虑到电离层折射改正的影响：，则有

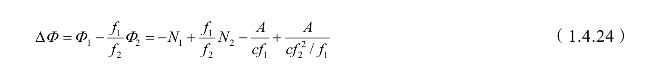
对双频载波相位观测值进行组合运算，同时考虑电离层折射改正，这样就消去了距离项和钟差项以及对流层的改正项，只剩下整周数之差与电离层折射的残差项，其值很小，所以此方法又称为电离层残差法。

此方法的优点在于ΔΦ只涉及频率，取决于电离层残差的影响，不用预先知道测站和卫星坐标。其缺点在于，如果两个载波相位观测值中都出现周跳无法使用此方法，而且不能顾及多路径效应和测量噪声的影响。

（5）根据平差后的残差发现和修复周跳。

根据上述方法处理后的观测值中可能还会存在一些未被发现的小周跳，修复后的观测值也可能有偏差。所以对于修复后的观测值再进行平差计算，求得其残差，有周跳的值会出现很大的残差，据此可以发现和修复周跳。