一、概　述

由GPS定位的原理可知，GPS定位是以GPS卫星为动态已知点，根据GPS接收机观测的星站距离来确定接收机或测站的位置。而位置的确定离不开坐标系。GPS定位所采用的坐标系与经典测量的坐标系相同之处甚多，但也有其显著的特点，主要如下：

（1）由于GPS定位以沿轨道运行的GPS卫星为动态已知点，而GPS卫星轨道与地面点的相对位置关系是时刻变化的，为了便于确定GPS卫星轨道及卫星的位置，须建立与天球固连的空固坐标系。同时，为了便于确定地面点的位置，还须建立与地球固连的地固坐标系。因而，GPS定位的坐标系既有空固坐标系，又有地固坐标系。

（2）经典大地测量是根据地面局部测量数据确定地球形状、大小，进而建立坐标系的，而GPS卫星覆盖全球，因而由GPS卫星确定地球形状、大小建立的地球坐标系是真正意义上的全球坐标系，而不是以区域大地测量数据为依据建立的局部坐标系，如我国“1980年国家大地坐标系”。

（3）GPS卫星的运行是建立在地球与卫星之间的万有引力基础上的，而经典大地测量主要是以几何原理为基础的，因而GPS定位中采用的地球坐标系的原点与经典大地测量坐标系的原点不同。经典大地测量是根据本国的大地测量数据进行参考椭球体定位，以此参考椭球体中心为原点建立坐标系，称为参心坐标系。而GPS定位的地球坐标系原点在地球的质量中心，称为地心坐标系。因而进行GPS测量，常需进行地心坐标系与参心坐标系的转换。

（4）对于小区域而言，经典测量工作通常无须考虑坐标系的问题，只需简单地使新点与已知点的坐标系一致便可；而GPS定位中，无论测区多么小，都涉及WGS-84地球坐标系与当地参心坐标系的转换问题。

由此可见，GPS定位中所采用的坐标系比较复杂。为便于学习掌握，可将坐标系进行如表1.2.1所示分类。

表1.2.1　GPS测量坐标系分类

二、天球坐标系

天球坐标系属于空固坐标系，是不随地球一起自转但随地球一起公转的坐标系，其坐标原点及各坐标轴指向在空间保持不变，便于描述天体及卫星的位置和运行状态。

1.天球的概念

以地球质心M为球心，以任意长为半径的假想球体称为天球。天文学中常将天体沿天球半径方向投影到天球面上，再根据天球面上的参考点、线、面来确定天体位置。天球面上的参考点、线、面如图1.2.1所示。

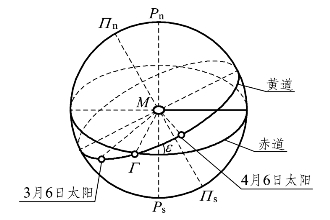
图1.2.1　天球的概念

（1）天轴与天极。

地球自转轴的延伸直线为天轴，天轴与天球面的交点称为天极，交点Pn为北天极，位于北极星附近，Ps为南天极。位于地球北半球的观测者，因地球遮挡不能看到南天极。

（2）天球赤道面与天球赤道。

通过地球质心M且垂直于天轴的平面称为天球赤道面，与地球赤道面重合。天球赤道面与天球面的交线称为天球赤道。

（3）天球子午面与天球子午圈。

包含天轴的平面称为天球子午面，与地球子午面重合。天球子午面与天球面的交线为一大圆，称为天球子午圈。天球子午圈被天轴截成的两个半圆称为时圈。

（4）黄道。

地球绕太阳公转的轨道面称为黄道面。黄道面与赤道面的夹角ε 称为黄赤交角，约为23.5°。黄道面与天球面相交成的大圆叫黄道，也就是地球上的观测者见到的太阳在天球面上的运行轨道。由于地球自转，对于地面上的观测者来说，天球赤道面不动而黄道面每日绕天轴旋转一周。又由于地球绕太阳公转，直观上看，太阳在黄道上每日自西向东运行约1°，每年运行一周。而斗柄在天球上的指向每年自东向西旋转一周。由于黄赤交角的缘故，在地球自转与公转的共同作用下产生了一年四季的变化。

（5）黄极。

通过天球中心且垂直于黄道面的直线与天球面的两个交点称为黄极，靠近北天极Pn的交点Πn称为北黄极，Πs称为南黄极。

（6）春分点。

当太阳在黄道上从天球南半球向北半球运行时，黄道与天球赤道的交点称为春分点，也就是春分时刻太阳在天球上的位置，如图1.2.1中的Γ。春分之前，春分点位于太阳以东。春分过后，春分点位于太阳以西。春分点与太阳之间的距离每日改变约1°。

2.天球坐标系

常用的天球坐标系有天球空间直角坐标系和天球球面坐标系。

天球空间直角坐标系的坐标原点位于地球质心。z轴指向北天极Pn，x轴指向春分点Γ，y轴垂直于xMz平面，与x轴和z轴构成右手坐标系。即伸开右手，大拇指和食指伸直，其余三指曲90°，大拇指指向z轴，食指指向x轴，其余三指指向y轴。在天球空间直角坐标系中，任一天体的位置可用天体的三维坐标（x，y，z）表示，见图1.2.2。

图1.2.2　天球空间直角坐标系与天球球面坐标系

天球球面坐标系的坐标原点也位于地球质心。天体所在天球子午面与春分点所在天球子午面之间的夹角称为天体的赤经，用α 表示；天体到原点M的连线与天球赤道面之间的夹角称为赤纬，用δ 表示；天体至原点的距离称为向径，用r表示。这样，天体的位置也可用三维坐标（α，δ，r）唯一确定。

3.岁差与章动的影响

地球绕自转轴旋转，在无外力矩作用时，其旋转轴指向应该不变。但由于日月对地球赤道隆起部分的引力作用，使得地球自转受到外力矩作用而发生旋转轴的进动现象。即从北天极上方观察时，北天极绕北黄极在圆形轨道上沿顺时针方向缓慢运动，致使春分点每年西移50.2″，25 800年移动一周。这种现象叫岁差。在岁差影响下的北天极称为瞬时平北天极，相应的春分点称为瞬时平春分点。瞬时平北天极绕北黄极旋转的圆称为岁差圆，见图1.2.3。

图1.2.3　岁差与章动

事实上，由于月球轨道和月地距离的变化，使实际北天极沿椭圆形轨道绕瞬时平北天极旋转，这种现象叫章动，周期为18.6年。在章动影响下，实际的北天极称为瞬时北天极，相应的春分点称为真春分点。瞬时北天极绕瞬时平北天极旋转的椭圆叫章动椭圆，长半径约为9.2″。

4.协议天球坐标系

由以上可知，北天极和春分点是运动的，这样，在建立天球坐标系时，z轴和x轴的指向也会随之运动，给天体位置的描述带来不便。为此，人们通常选择某一时刻作为标准历元，并将标准历元的瞬时北天极和真春分点作章动改正，得z轴和x轴的指向，这样建立的坐标系称为协议天球坐标系。国际大地测量学协会（IAG）和国际天文学联合会（IAU）决定，从1984年1月1日起，以2000年1月15日为标准历元。也就是说，目前使用的协议天球坐标系，其z轴和x轴分别指向2000年1月15日的瞬时平北天极和瞬时平春分点。为了便于区别，z轴和x轴分别指向某观测历元的瞬时平北天极和瞬时平春分点的天球坐标系，称为平天球坐标系；z轴和x轴分别指向某观测历元的瞬时北天极和真春分点的天球坐标系称为瞬时天球坐标系。

为了将协议天球坐标系的坐标转换为瞬时天球坐标系的坐标，须经过如下两个步骤的坐标转换。

（1）将协议天球坐标系的坐标转换为瞬时平天球坐标系的坐标。

以　和分别表示天体在瞬时天球坐标系和协议天球坐标系中的坐标，因两坐标系原点同为地球质心，所以只要将协议天球坐标系的坐标轴旋转三次，便可转换为瞬时天球坐标系的坐标。转换公式如下：

式中，ζ、θ、z为坐标系绕z轴和x轴旋转的角度，其值由观测历元与标准历元之间的时间差计算。负号表示旋转向量与该坐标轴方向相反，无负号表示旋转向量与该坐标轴方向相同。为坐标变换矩阵。

（2）将瞬时平天球坐标系的坐标转换为瞬时天球坐标系的坐标。

以　表示瞬时天球坐标系的坐标，则转换公式如下：

式中，ε为观测历元的平黄赤交角；Δψ，Δε分别为黄经章动和交角章动。

三、地球坐标系

地球坐标系为固连在地球上，并与地球一起公转和自转的坐标系，便于描述地面点的位置，又称地固坐标系。

地球坐标系根据坐标系原点位置的不同，又分为地心坐标系和参心坐标系。

地球坐标系根据表现形式不同，又分为空间直角坐标系与大地坐标系。

1.地心坐标系

地心坐标系是以地球质心（包括海洋和大气的整个地球的质量中心）为原点的坐标系，其椭球中心与地球质心重合，且椭球定位与全球大地水准面最为密合。相对于参心坐标系，地心坐标系是全球性的坐标系。

通常有两种表现形式：地心空间直角坐标系与地心大地坐标系。

目前常用的WGS-84坐标系和2000国家大地坐标系均属于地心坐标系。

（1）WGS-84坐标系。

WGS-84坐标系是美国根据卫星大地测量数据建立的大地测量基准，是目前GPS所采用的坐标系。GPS卫星发布的星历就是基于此坐标系，用GPS所测的地面点位，如不经过坐标系的转换，也是此坐标系中的坐标。WGS-84坐标系定义如表1.2.2所示。

表1.2.2　WGS-84坐标系定义

（2）2000国家大地坐标系。

我国于2008年7月1日起，全面启用“2000国家大地坐标系”。2000国家大地坐标系的建立，标志着我国测绘科学技术取得了巨大进步，从此进入了一个崭新的发展阶段，体现了世界级的先进水平，2000国家大地坐标系定义如表1.2.3所示。

表1.2.3　2000国家大地坐标系定义

（3）ITRF国际参考框架。

国际地球参考框架ITRF是一个地心参考框架，是目前精度最高、影响最大的地球参考框架。国际地球自转服务组织（IERS）每年将其所属全球站的观测数据进行综合处理分析，得到一个ITRF框架，并以IERS年报和IERS技术备忘录的形式发布。自1988年起，IERS已经发布了ITRF88、ITRF89、ITRF90、ITRF91、ITRF92、ITRF93、ITRF94、ITRF96、ITRF97、ITRF2000等全球坐标参考框架。各框架在原点、定向、尺度及时间演变基准的定义上有微小差别。

目前ITRF参考框架已在世界上得到广泛应用，我国各地建立的网络系统也为用户提供ITRF框架的转换服务。

2.参心坐标系

在经典大地测量中，为了处理观测成果和传算地面控制网的坐标，通常须选取一参考椭球作为基本参考面，选一参考点作为大地测量的起算点（称为大地原点），利用大地原点天文观测量来确定参考椭球在地球内部位置和方向。由此确定的参考椭球，其中心一般不会和地球质心重合。这种坐标原点位于参考椭球中心的坐标系称为参心坐标系。相对于地心坐标系，参心坐标系又称为区域坐标系。

同样，参心坐标系也有两种表现形式：参心直角坐标系和参心大地坐标系。

由于参心坐标系所采用的参考椭球不同、参考椭球的定位与定向不同，因而有不同的参心坐标系。我国常用的参心坐标系有：1954年北京坐标系和1980年国家大地坐标系。

（1）1954年北京坐标系。

1954年北京坐标系在一定意义上可看成是苏联1942年坐标系的延伸，见表1.2.4。其建立方法是，依照1953年我国东北边境内若干三角点与苏联境内的大地控制网连接，将其坐标延伸到我国，并在北京市建立了名义上的坐标原点，并定名为“1954年北京坐标系”（简称北京54坐标系）。以后经分区域局部平差，扩展、加密而遍及全国。因此，1954年北京坐标系，实际上是苏联1942年坐标系，原点不在北京，而在苏联的普尔科沃。

表1.2.4　1954年北京坐标系定义

几十年来，我国按1954年北京坐标系建立了全国大地控制网，完成了覆盖全国的各种比例尺地形图，以满足经济、国防建设的需要。由于各种原因，1954年北京坐标系存在如下主要缺点和问题：

①克拉索夫斯基椭球体长半轴（a＝6 378 245 m）比1975年国际大地测量与地球物理联合会推荐的更精确地球椭球长半轴（a＝6 378 140 m）大105 m。

②1954年北京坐标系所对应的参考椭球面与我国大地水准面存在着自西向东递增的系统性倾斜，高程异常（大地高与海拔高之差）最大为+65 m（全国范围平均为29 m），且出现在我国东部沿海经济发达地区。

③提供的大地点坐标，未经整体平差，是分级、分区域的局部平差结果，使点位之间（特别是分别位于不同平差区域的点位）的兼容性较差，影响了坐标系本身的精度。

（2）1980年国家大地坐标系。

针对1954年北京坐标系的缺点和问题，1978年我国决定建立新的国家大地坐标系，该坐标系取名为“1980年国家大地坐标系”（简称西安80坐标系）。该大地坐标系原点设在处于我国中心位置的陕西省西安市泾阳县永乐镇，位于西安市西北方向约60 km处，简称“西安原点”。1980年国家大地坐标系定义如表1.2.5。

表1.2.5　1980年国家大地坐标系定义

该坐标系的主要优点如下：

①地球椭球体元素，采用1975年国际大地测量与地球物理联合会推荐的更精确的参数。

②椭球定位以我国范围高程异常值平方和最小为原则求解参数，椭球面与我国大地水准面获得了较好地吻合。高程异常平均值由1954年北京坐标系的29 m减至10 m，最大值出现在西藏的西南角（+40 m），全国广大地区多数在15 m以内。

③全国整体平差，消除了分区局部平差对控制的影响，提高了平差结果的精度。

④大地原点选择在我国中部，缩短了推算大地坐标的路程，减少了推算误差的积累。

不可否认，建立1980年国家大地坐标后，也带来了新的问题和附加工作，主要体现在地形图图廓线和方里网线位置的改变，改变大小随点位而异，我国东部地区其变化最大约为80 m，平均约为60 m。图廓线位置的改变，使新旧地形图接边时产生裂隙。如80 m的变化，在1∶5万地形图上表现为1.6 mm、在1∶1万地形图上表现为8 mm。方里线位置的改变，不仅与坐标系的变化有关，而且还包括因椭球参数改变所带来的投影后平面坐标变化的影响。

3.空间直角坐标系与大地坐标系

无论是天球坐标系或地球坐标系，还是地心坐标系或参心坐标系，按表现形式又可以分为空间直角坐标系与大地坐标系。

空间直角坐标系的坐标原点位于地球质心（地心坐标系）或参考椭球中心（参心坐标系），以笛卡尔坐标的形式，z轴、x轴、y轴构成右手坐标系。

大地坐标系是用大地经度L、大地纬度B和大地高H表示地面点位的。过地面点P的子午面与起始子午面间的夹角叫P点的大地经度。由起始子午面起算，向东为正，叫东经（0°～180°）；向西为负，叫西经（0°～-180°）；过P点的椭球法线与赤道面的夹角叫P点的大地纬度。由赤道面起算，向北为正，叫北纬（0°～90°），向南为负，叫南纬（0°～90°）。从地面点P沿椭球法线到椭球面的距离叫大地高。

地面上任意点的位置，在空间直角坐标系中坐标表示为（x，y，z）P；在大地坐标系中坐标表示为（B，L，H）P。两种坐标的关系如图1.2.4所示。

图1.2.4　地球空间直角坐标系与大地坐标系

4.高斯-克吕格平面直角坐标系

空间直角坐标系和大地坐标系不便于在平面上表达空间点的位置关系，因此，为了便于绘制平面图形，地面点应沿椭球法线投影到椭球面上，再通过地图投影方式，将椭球面上的点投影到平面上。我国统一规定：1∶50万以及更大比例尺地形图采用高斯-克吕格投影。

高斯-克吕格投影属于横轴等角切椭圆柱投影。其原理是：假设用一个椭圆柱面横向套在地球上，使椭圆柱面的轴线通过地心，椭圆柱面与地球椭球面某一经线相切，此经线称为中央经线，以这种椭圆柱面作为投影面。地面点的位置最终以平面坐标x、y和高程H表示，见图1.2.5。

图1.2.5　高斯-克吕格投影的几何概念

为了使变形控制在一个较小的范围内，该投影采用分带投影的办法，即在中央经线东西两侧3°作为一个投影带，投影带的边界即为中央经线东西两侧3°的经线。两条经线在地球南北极相交，形成如同一个花瓣形状的条带。将这样的条带内的地表地物点位逐一投影到椭圆柱面上，然后将此条带展开铺平，再缩小，将其按一定要求分割形成地图。在椭圆柱面内“旋转”地球球面，旋转角度6°，又形成另一花瓣形状的条带，又可生成这一条带区域内的地图。总共旋转60次，就可以将地球每一个区域囊括，如图1.2.6所示。这就是高斯-克吕格投影分带制作地图的原理。

图1.2.6　高斯-克吕格投影分带示意图

以上面方法，制作1∶2万～1∶50万地形图采用6°分带；1∶1万以及更大比例尺地形图采用3°分带，以保证必要的精度。在6°分带或3°分带以内，由于地图图幅的限制，按照比例尺的不同，对每一分带还要按经线与纬线进行分幅。

5.地方坐标系

高斯-克吕格平面直角坐标系在建立过程中，会产生以下两种变形：

（1）高程归化变形。

由于椭球面上两点的法线不平行，在不同高度上测量两点的两条法线之间的距离也不相同，高度越大，距离越长。如图1.2.7所示，将A、B两点沿法线投影到椭球面上，会引起椭球面上的距离DAB与地面上的距离SAB不等，其差值称为高程归化变形。对于一般工程而言，（SAB-DAB）/DAB应不超过1/40 000。因（SAB-DAB）/DAB＝H/R，由此求得H应不超过160 m。

在我国东部沿海地区，地面高程一般较小，可以不考虑高程归化变形。而对于中西部地区，地面高程较大，高程归化变形导致图上长度与实地长度相差过大，不利于工程建设。所以需要用测区平均高程面代替椭球面，将地面点沿法线投影到测区平均高程面上之后，再进行高斯投影。例如，某测区地面到北京54椭球的距离为1 500～1 800 m，则可选择1 650 m的高程面作为测区平均高程面，也就是将北京54的椭球长半径由6 378 245 m增大到63 279 895 m，而椭球扁率仍为1/298.3。

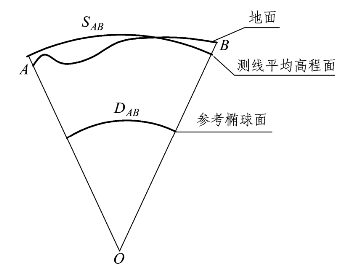
图1.2.7　高程归化变形

（2）高斯投影长度变形。

在高斯投影时，中央子午线投影后长度不变，离中央子午线越远，长度变形越大。设A、B两点在椭球面上的长度为DAB，在高斯平面上的长度为LAB，则

一般工程要求这一变形不超过1/40 000，由此求得AB离中央子午线的距离应不超过45 km。对于国家3°带，离中央子午线的最大距离可达167 km。所以，当测区到中央子午线的距离超过45 km时，应重新选择中央子午线。例如，某测区经度为106°12′～106°30′，则该测区所在3°带中央子午线经度为105°，测区纬度为32°30′～32°38′，该测区离3°带中央子午线的最大距离为150 km，因此，在高斯投影时应另行选择中央子午线经度为106°21′。

综上所述，当测区高程大于160 m或离中央子午线距离大于45 km时，不应采用国家统一坐标系而应建立地方坐标系。建立地方坐标系最简单的方法如下：

①选择测区任意带中央子午线经度，使中央子午线通过测区中央，并对已知点的国家统一坐标（xi，yi）进行换带计算，求得已知点在该带中的坐标（xi′，yi′）。

②选择测区平均高程面的高程h0，使椭球长半径增大h0，或者将已知点在任意带中的坐标增量增大（1+h0/R）倍，求得改正后坐标增量Δx′、Δy′

③选择一个已知点作为坐标原点，使该点坐标仍为任意带坐标不变，即

或者给原点坐标加一个常数

或者直接取原点坐标为某值。(www.daowen.com)

④其他各已知点坐标按原点坐标和改正后坐标增量计算，即

由于高程归化变形与高斯投影变形的符号相反，所以，可将地面长度投影到参考椭球面而不选择测区平均高程面，用适当选择投影带中央子午线的方法抵消高程归化变形；也可使中央子午线与国家统一坐标的中央子午线一致，而通过适当选择高程面来抵消高斯投影变形。

6.地极移动与协议地球坐标系

由于地球不是刚体，在地幔对流以及其他物质迁移的影响下，地球自转轴相对于地球体发生移动，这种现象叫地极移动，简称极移。在建立地球坐标系时，如果使z轴指向某一观测时刻的地球北极，这样的地球坐标系称为瞬时地球坐标系。显然，瞬时地球坐标系并未与地球固连，因此，地面点在瞬时地球坐标系中的位置也是变化的。

为了比较简明地描述地极移动规律，国际纬度局根据1900—1905年5个国际纬度站的观测结果取平均，定义了协议原点（CIO）。过CIO作地球切平面，并以CIO为原点建立平面直角坐标系，其中xP轴指向格林尼治方向，yP轴指向西经90°方向。某一观测时刻的地极位置可用瞬时地极坐标xP和yP表示。国际地球自转服务组织（IERS）定期公布瞬时地极坐标和各年度的平均地极坐标，图1.2.8为1995—1998年的地极移动情况。

图1.2.8　1995—1998年地极移动轨迹

以CIO为参照，国际时间局（BIH）等其他国际组织也根据观测数据定义了不同的协议地极，如BIH84.0等。

z轴指向协议地球北极的地球坐标系称为协议地球坐标系。瞬时地球坐标系与协议地球坐标系之间的坐标可通过式（1.2.8）转换：

在GPS测量中，为确定地面点的位置，需要将GPS卫星在协议天球坐标系中的坐标转换为协议地球坐标系中的坐标，转换步骤为：协议天球坐标系→瞬时平天球坐标系→瞬时天球坐标系→瞬时地球坐标系→协议地球坐标系。其中，除第三步由瞬时天球坐标系转换为瞬时地球坐标系外，其他步骤的转换方法前已述及，此处只介绍第三步的转换。

瞬时天球坐标系与瞬时地球坐标系的坐标原点相同，z轴指向相同，只是两坐标系的x轴在赤道上有一夹角，角值为春分点的格林尼治恒星时。因此只需将瞬时天球坐标系绕z轴旋转春分点的格林尼治恒星时时角GAST即可。计算公式如下：

四、高程系统

1.正高

所谓正高，是指地面点沿铅垂线到大地水准面的距离。如图1.2.9所示，B点的正高为

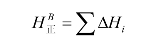
图1.2.9　正高系统

由于水准面不平行，从O点出发，沿OAB路线用几何水准测量B点高程，显然

为此，应在水准路线上测量相应的重力加速度gi，则B点的正高为

式（1.2.10）中的g和dh可在水准路线上测得，而为B点不同深度处的重力加速度平均值，只能由重力场模型确定，在没有精确的重力场模型的情况下，无法求得。

2.正常高

在式（1.2.10）中，用B点不同深度处的正常重力加速度代替实测重力加速度，可得B点正常高：

从地面点沿铅垂线向下量取正常高所得曲面称为似大地水准面。我国采用正常高系统，也就是说，我国的高程起算面实际上不是大地水准面而是似大地水准面。似大地水准面在海平面上与大地水准面重合，在我国东部平原地区，两者相差若干厘米，在西部高原地区相差若干米。

3.大地高

地面点沿椭球法线到椭球面的距离叫该点的大地高，用H表示。大地高与正常高有如下关系：

式中　N——大地水准面差距；

ξ——高程异常。

五、坐标系统的转换

GPS采用WGS-84坐标系，而在工程测量中所采用的是北京54坐标系或西安80坐标系或地方坐标系。因此需要将WGS-84坐标系转换为工程测量中所采用的坐标系。

1.同一坐标系下不同坐标形式的转换

同一坐标系下不同坐标形式的转换包括空间直角坐标（X，Y，Z）和大地坐标（B，L，H）的相互转换、高斯平面直角坐标（x，y）和大地坐标（B，L）的相互转换两种类型。

（1）空间直角坐标和大地坐标的转换。

在相同的基准下，将空间大地坐标转换为空间直角坐标公式为

式中　N——卯酉圈的半径。

式中　a——地球椭球的长半轴；

b——地球椭球的短半轴。

在相同的基准下，将空间直角坐标转换成为空间大地坐标的公式为

在采用上式进行转换时，需要采用迭代的方法，先利用下式求出B的初值：

然后，利用该初值求定H、N的初值，再利用所求出的H和N的初值再次求定B值。

将空间直角坐标转换成为空间大地坐标也可以采用如下的直接算法：

其中

（2）高斯平面直角坐标和大地坐标的转换。

由经纬度计算高斯平面直角坐标称为高斯正算，公式如下：

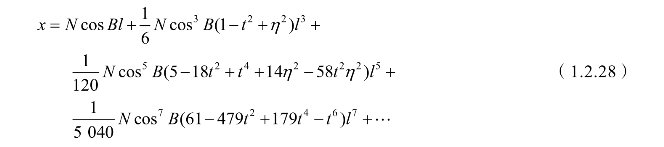
式中　l （B）——子午线弧长；

N=——卯酉圈半径；

t——t=antB；

l=L-L0——经差；

L0——中央子午线经度。

l（B）——从赤道到投影点的椭球面弧长，可用下式计算：

其中

和

由高斯平面直角坐标计算经纬度称为高斯反算，公式如下：

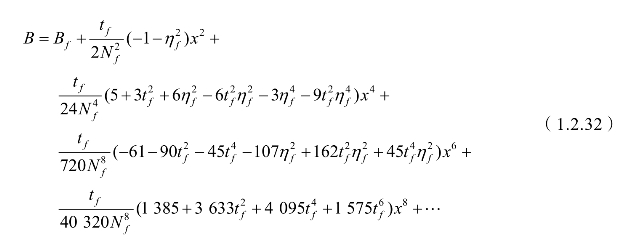
其中，下标为f的项需要基于底点纬度　fB来计算。关于底点纬度的计算，可以采用下面的级数展开式计算：

其中

且

2.不同坐标系的转换

由于GPS采用WGS-84坐标系，而我国各地常用的坐标系是1954年北京坐标系、1980年国家大地坐标系和地方坐标系，因此，无论测区范围多小，测量精度等级如何低，都会涉及不同坐标系统之间的转换问题。

（1）空间直角坐标系的转换。

如图1.2.10所示，WGS-84坐标系的坐标原点为地球质量中心，而北京54坐标系和西安80坐标系的坐标原点是参考椭球中心。所以在两个坐标系之间进行转换时，应进行坐标系的平移，平移量可分解为Δx0、Δy0和Δz0。又因为WGS-84坐标系的三个坐标轴方向也与北京54坐标系或西安80坐标系的坐标轴方向不同，所以还需将北京54坐标系或西安80坐标系分别绕x轴、y轴和z轴旋转ωx、ωy、ωz。此外，两坐标系的尺度也不相同，还需进行尺度转换。两坐标系间转换的公式如下：

图1.2.10　空间直角坐标系的转换

式中，m为尺度比因子。

要在两个空间直角坐标系之间转换，需要知道三个平移参数（Δx0，Δy0，Δz0），三个旋转参数（ωx，ωy，ωz）以及尺度比因子m。为求得七个转换参数，在两个坐标系中至少应有三个公共点，即已知三个点在WGS-84坐标系中的坐标和在北京54坐标系或西安80坐标系中的坐标。在求解转换参数时，公共点坐标的误差对所求参数影响很大，因此所选公共点应满足下列条件：

①点的数目要足够多，以便检核；

②坐标精度要足够高；

③分布要均匀；

④覆盖面要大，以免因公共点坐标误差引起较大的尺度比因子误差和旋转角度误差。

在WGS-84坐标系与北京54坐标系或西安80坐标系之间进行转换，除上述七参数外，还应给出两坐标系的两个椭球参数，一个是长半径，另一个是扁率。

以上转换步骤中，计算人员只需输入七个转换参数或公共点坐标、椭球参数、中央子午线经度和x、y加常数即可，其他计算工作由软件自动完成。

（2）平面直角坐标系的转换。

如图1.2.11所示，在两平面直角坐标系之间进行转换，需要有四个转换参数，其中两个平移参数（Δx0，Δy0），一个旋转参数α 和一个尺度比因子m。转换公式为

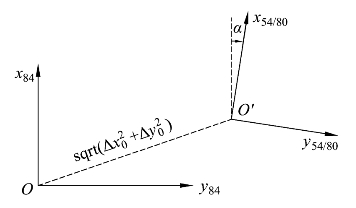
图1.2.11　平面直角坐标系的转换

为求得四个转换参数，应至少有两个公共点。

对于不同坐标系之间的坐标转换，平面四参数转换模型原理简单，数值稳定可靠；对较小区域，其转换的精度较高，但当范围较大时，由于受投影变形误差的影响，其转换精度就较差，因而它只适合于较小区域的坐标转换。七参数转换模型为三维模型，在空间直角坐标系中，两坐标系之间存在严密的转换模型；由于理论比较严密，不存在模型误差和投影变形误差，因而它适合于任何区域的坐标转换。

3.高程系统的转换

GPS所测得的地面高程是以WGS-84椭球面为高程起算面的，而我国的1956年黄海高程系和1985年国家高程基准是以似大地水准面作为高程起算面的，所以必须进行高程系统的转换。使用较多的高程系统转换方法是高程拟合法、区域似大地水准面精化法和地球模型法。因目前还没有适合于全球的大地水准面模型，所以此处只介绍前两种方法。

（1）高程拟合法。

虽然似大地水准面与椭球面之间的距离变化极不规则，但在小区域内，用斜面或二次曲面来确定似大地水准面与椭球面之间的距离还是可行的。

①斜面拟合法。

由式（1.2.12）知，大地高与正常高之差就是高程异常ξ，在小区域内可将ξ看成平面位置x、y的一阶函数，即

或

如果已知至少三个点的正常高H常并测出其大地高H，则可解出式（1.2.38）中的系数a、b、c，然后便可根据任一点的大地高按式（1.2.40）求得相应的正常高。

②二次曲面拟合法。

二次曲面拟合法的方程式为

如已知至少六个点的正常高并测得大地高，便可解出a、b、…、f等六个参数，然后根据任一点的大地高便可求得相应的正常高。

（2）区域似大地水准面精化法。

区域似大地水准面精化法就是在一定区域内采用精密水准测量、重力测量及GPS测量，先建立区域内精确的似大地水准面模型，然后便可根据此模型快速准确地进行高程系统的转换。精确求定区域似大地水准面是大地测量学的一项重要科学目标，也是一项极具实用价值的工程任务。我国高精度省级似大地水准面精化工作正在部分省、市展开，如江苏、青岛、深圳等省市已建成厘米级的区域似大地水准面模型。在具有如此高精度的似大地水准面模型的地方，用GPS测高程可代替三等水准。