由于制动盘（鼓）边界上热载荷的交变特性，进行温度场全三维仿真实际是一个复杂的“四维”问题。因此全三维瞬态热力学仿真计算较之常规的热力学分析工作量成几何数量级的增长，给制动系统虚拟设计的高效求解带来了困难。因此需要对力学模型进行简化，开发快速仿真模型。在制动盘（鼓）上到中心距离相等的同心环上任意两点A、B的载荷如图7-44所示。制动盘（鼓）结构上存在循环对称轴和周期角，并且绕此轴旋转任意一个周期角时，旋转前后的结构重合，物理参数和边界条件也完全重合。

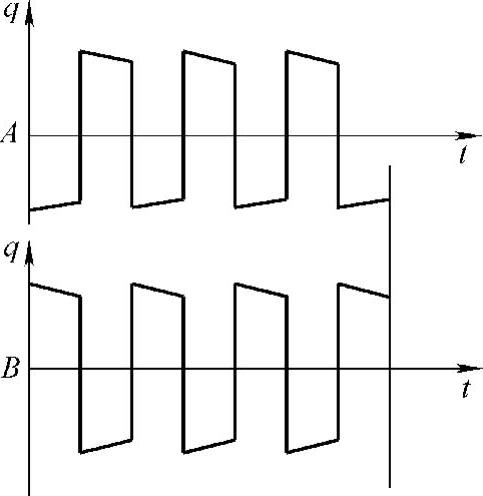
图7-44 A、B点热流函数曲线对比图

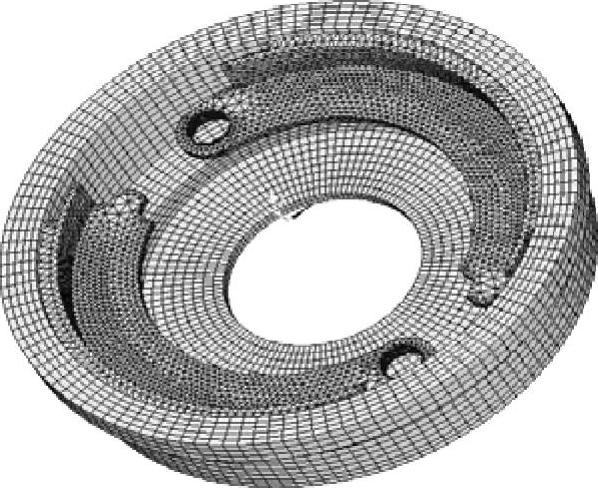
图7-45 制动鼓的整体热力学模型

循环制动过程中，制动系统的温度达到了400℃甚至更高，此时必须考虑辐射边界条件。具有循环对称特征的构件的温度场的求解可以化为对称边界下的一般结构的泛函变分极值问题，从而可以方便地利用热力学法求解。对完全循环对称式的制动鼓，可以直接采用二维热力学模型，如图7-45所示。对于完全循环对称式的实心式制动盘，可以直接采用二维热力学模型，如图7-46所示。对于空心盘式制动系统，考虑散热筋板结构，建立自通风式三维循环对称热力学模型，如图7-47所示。在制动过程中，电动汽车的动能通过轮胎与地面之间的滑动摩擦力和制动系统摩擦副之间的摩擦生热耗散。对于安装有ABS的电动汽车，希望通过制动系统摩擦副耗散的制动能量最大，这样就能将滑移率控制在最佳的滑移率上，保证电动汽车的制动稳定性。基于这一实际工况，一般将滑移率s通过ABS控制在10%左右，即认为在制动过程中90%的热量通过制动系统摩擦生热耗散。根据制动过程中的能量转换，得到任意时刻电动汽车上前、后制动系统上因为制动摩擦生热产生的热流密度为

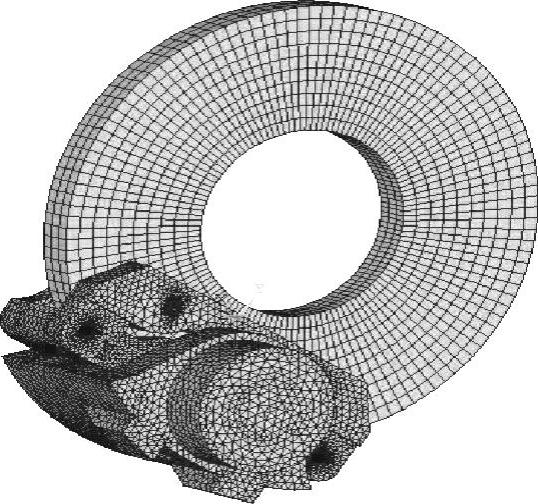
图7-46 实心盘式制动系统整体热力学模型

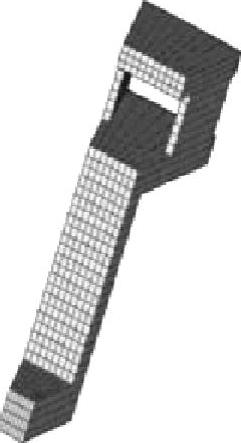
图7-47 空心盘式热力学模型

前制动系统

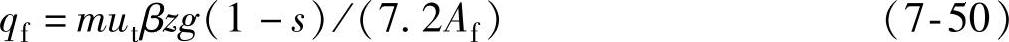
后制动系统

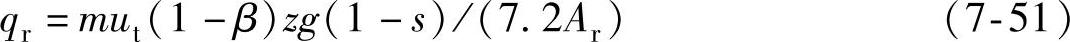
式中，u_t为循环制动过程中电动车辆的瞬时速度。根据制动系统台架试验方法（国标QC/T 564）得

u_t=u₀-at（7-52）

式中，m为车质量；β为制动力分配系数；z为制动强度；s为滑移率；A_f为前制动盘总工作面积；A_r为后制动盘总工作面积。

在制动过程中，制动产生的热量将在制动系统接触副之间进行分配。基于前面的循环对成理论，总的热量在制动衬块和制动盘（鼓）之间分配系数为

(www.daowen.com)

式中，q_r、ρ_r、C_r、K_r分别为制动盘（鼓）的热流密度函数、密度、比热、导热系数；q_k、ρ_k、C_k、K_k分别为制动系统摩擦块的热流密度函数、密度、比热、导热系数。因为密度、比热、导热系数是温度的函数，所以热载荷的分配系数ξ为温度的函数。实心制动盘与外界对流换热系数为

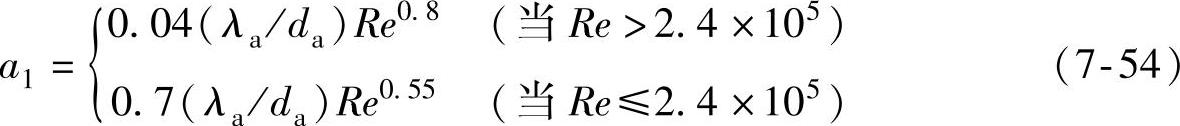
式中，Re=u_aρ_ad_a/（3.6μ_t）为雷诺数；ρ_a为空气的密度；μ_a为空气的黏度；λ_a为空气导热系数；d_a为制动盘的外径。空心盘式制动系统的对流换热系数包括制动盘的对流换热系数α₁和自然通风孔的对流换热系数α₂之和。通风孔的对流换热系数为

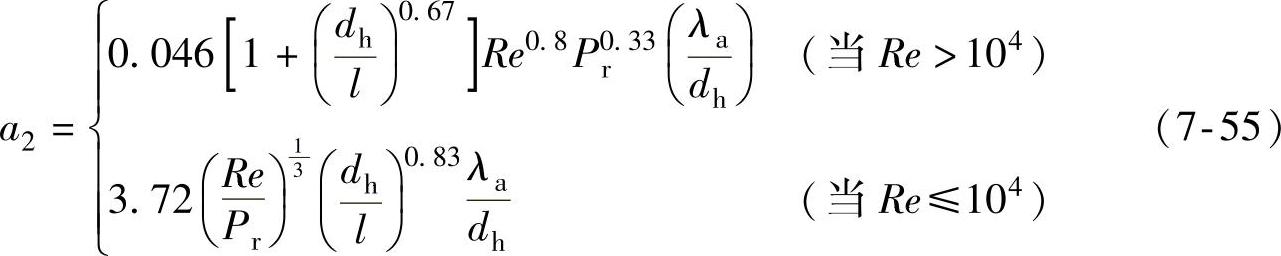
式中，l为制动盘的长度，l=（d_a-d_i）/2；d_h为流体力学直径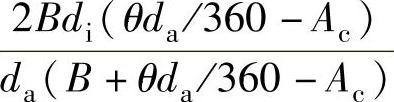，；v_q为风孔中气流的平均速度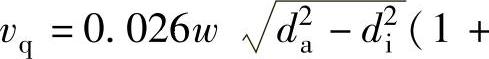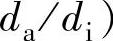，；Re为雷诺数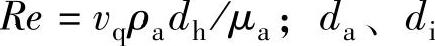，为空心制动盘的外径、内径，B为通风槽的宽度，h为制动盘的厚度，Ac为摩擦片的衬片面积，θ为摩擦片包角；w为制动系统的转速。因此，空心盘总的对流换热系数为a=a₁+a₂。鼓式制动系统制动鼓的旋转圆周表面部分和外界的换热系数与实心盘换热条件相似，所以a=a₁，而以Z轴为旋转轴的直径为D的制动接触表面的换热系数（Re≥1000）为

辐射的热流密度为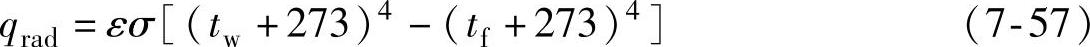

式中，q_rad为辐射热流密度；t_w为制动盘（鼓）温度；t_f为环境温度；ε为摩擦辐射流系数，对于制动盘（鼓）取0.55；σ为斯蒂芬-玻尔兹曼常数，5.67×10^-8W/m²k⁴。在进行热力学仿真计算过程中，由于辐射换热是一个高度非线性的问题，求解过程难以收敛。为此，将辐射换热等效为对流换热，式（7-57）等效为

q_rad=a_eqr（t_w-t_f）（7-58）

式中，a_eqr=εσ[（t_w+273）2+（t_f+273）2]（t_w+t_f+546）

以后制动系统为例，当制动盘（鼓）接触面处于制动接触时段时，输入的热流密度为

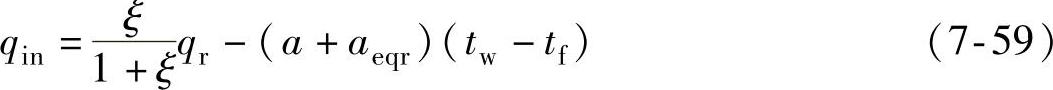
制动盘（鼓）接触面处于非制动接触时段，以及制动盘（鼓）非接触面输出热流密度为

q_out=（a+a_eqr）（t_w-t_f）（7-60）式中，a为对流换热系数，根据不同制动系统结构的不同部位，分别对应参数a₁、a₁+a₂、a₃。

15次制动循环的温度循环曲线如图7-48所示。图中曲线表示的是制动系统制动副接触面上不同位置上两点的温度曲线。经历了15次循环制动后，制动鼓上瞬变的温度场达到动态平衡。

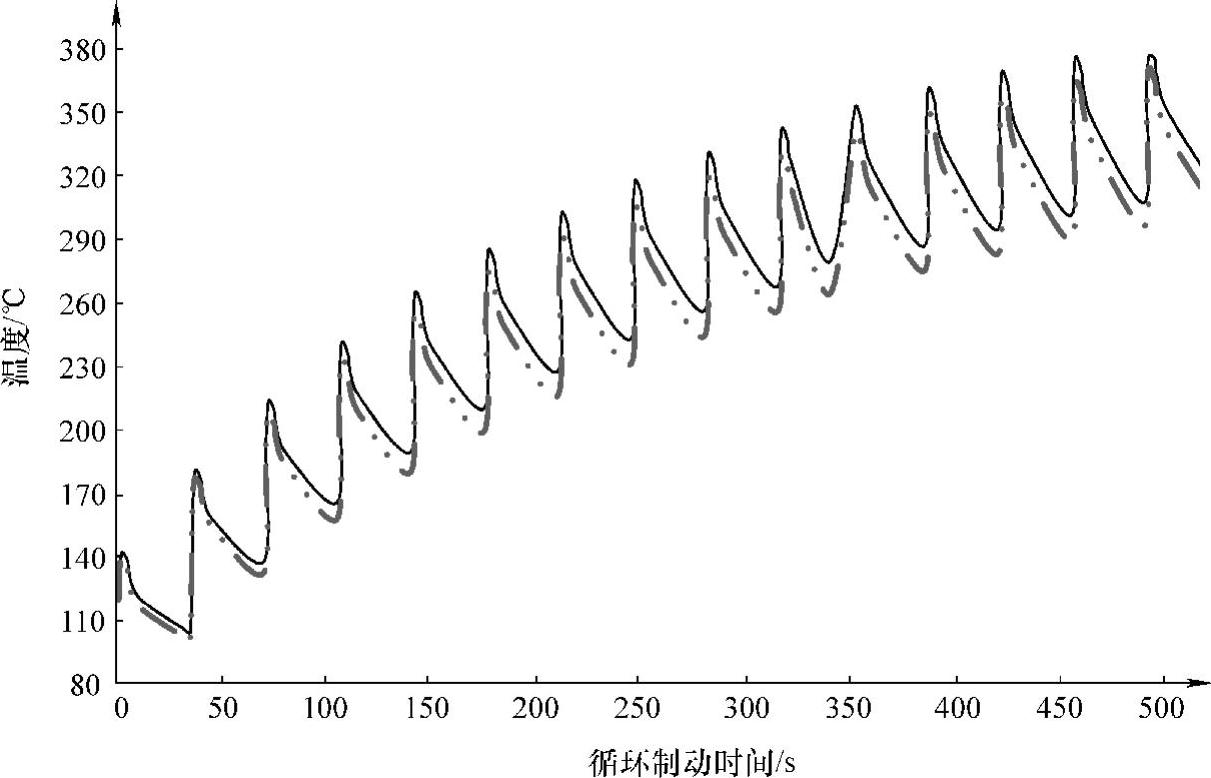
图7-48 15次循环制动制动接触面温度曲线

为了验证力学模型的正确性，在相同的工况下，在具有国际先进水平的SCHENCK（PWDOCPVO75O200）惯性式制动系统测功机上进行了15次循环制动试验测试，将仿真结果和测试结果进行了对比分析，仿真结果和测试结果均为循环过程中摩擦副的最高温度。结果表明：热力学仿真模型具有较高的精确度，循环温度的试验结果和分析结果变化规律一致，二者的偏差在5%以内，因而采用热力学方法分析制动能量回收循环中的问题是有效的和可行的。