系统模型是对实际系统的一种抽象，是对系统本质（或是系统的某种特性）的一种描述。模型应具有与系统相似的特性。好的模型能够反映实际系统的主要特征和运动规律（系统的某种特性）。系统模型可以分为实体模型和力学模型。力学模型包括原始系统模型和仿真系统模型。原始系统模型是对系统的原始描述。仿真系统模型是一种适合于在计算机上演算的模型，主要是指根据计算机的运算特点、仿真方式、计算方法、精度要求将原始系统模型转换为计算机程序。本章研究的电动车辆BERS结构模型，如图7-6所示。

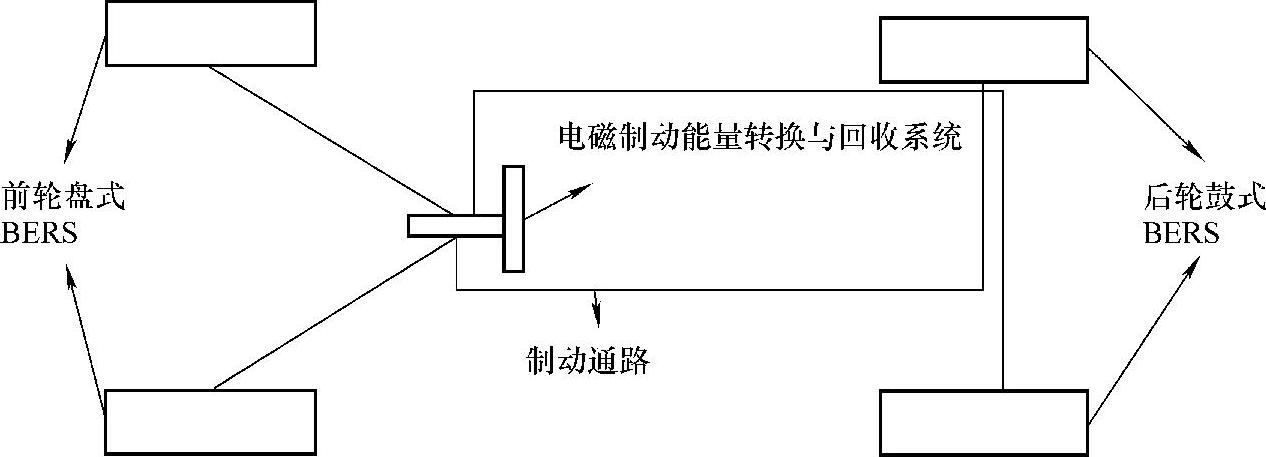
图7-6 电动车辆BERS结构简图

该电动车辆制动系统由电磁制动能量转换与回收系统，前轮盘式BERS和后轮鼓式BERS组成。其制动过程如图7-7所示。

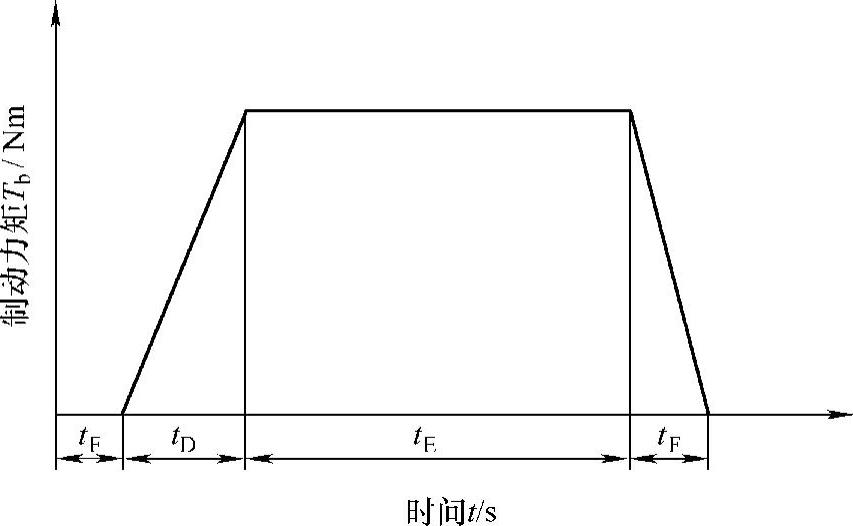
图7-7 电动车辆制动能量回收过程中制动力矩的变化

图中t_A为电动车辆制动系统反应时间，是指制动踏板踩下后，克服自由行程、机械阻力及电磁铁间间隙的时间。一般液压制动系统的反应时间为0.015～0.03s，气压制动系统的反应时间为0.05～0.06s，而BERS的反应时间为0.006～0.01s。t_D为制动起作用时间，这期间作用在车轮上的制动力矩不断增大，一般液压电动车辆制动系统起作用的时间为0.15～0.3s，气压电动车辆制动系统起作用的时间为0.3～0.8s，而BERS起作用的时间为0.01～0.05s；t_E为持续稳定制动时间，此阶段占整个制动过程的80%的时间以上且制动过程相对稳定；t_F为放松制动时间，此阶段驾驶人松开制动踏板，至此制动过程结束。

本章主要研究电动车辆的BERS的制动性能，采用单轮电动车辆模型，以使模型简化，使制动性能的研究更容易且不受其他条件干扰。对被控对象做如下假设：电动车辆的质量均匀地分布在每个车轮上；电动车辆在平坦的路面上行驶，忽略空气阻力和车轮的滚动阻力；忽略侧向力；不考虑制动过程的振动和由此引起的法向载荷的变化；不考虑电动车辆由于绕直线旋转或者是其他车轮上不均匀制动而造成的运动动力学。

整车及轮胎受力分析如图7-8所示，根据达朗伯原理，对模型中车体在行驶方向和车轮绕主轴方向两个自由度建立动力学方程，可得简化电动车辆动力学方程为

电动车辆运动方程：

车轮运动方程：

车轮纵向摩擦力：

制动力矩：

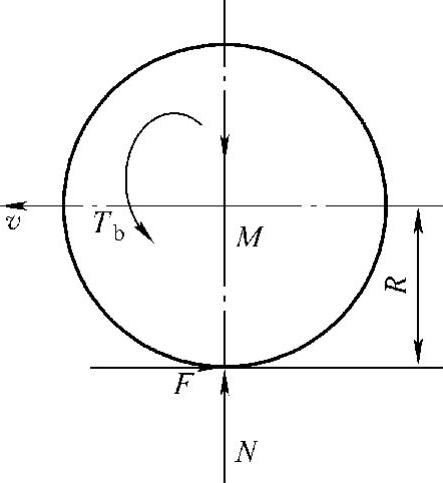
图7-8 单轮电动车辆模型(www.daowen.com)

式中，M为车轮的承载质量，即1/4车体质量；v为电动车辆车身行驶速度；F为车轮摩擦力；I为车轮转动惯量；R为车轮滚动半径；ω为车轮角速度；T_b为制动力矩即制动系统摩擦力矩；N为车轮对地面的法向反力；μ为车轮与地面间的附着系数；K为制动系统制动因数；t为时间。考虑轮胎模型魔术公式的表达式为

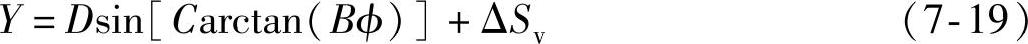
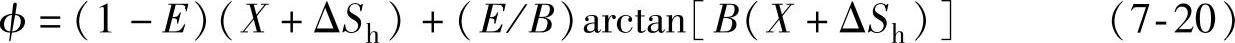
式中，D为峰值因子，表示曲线的最大值；B为刚度因子；E为曲线曲率因子，表示曲线最大值附近的形状；C为曲线形状因子，即曲线是像横向力、纵向力还是回正力矩；S_h为曲线的水平方向漂移；S_v为曲线垂直方向漂移。魔术公式模型用来模拟制动时车轮纵向附着系数和车轮滑移率之间的关系为：

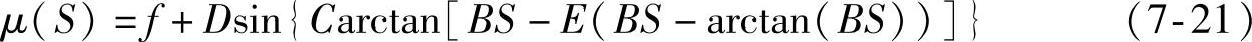
式中，f为轮胎的静摩擦系数；S为滑移率；μ为纵向附着系数。

若将纵向附着系数μ表示成滑移率S的函数，其表达式为

式中，B、C、D与魔术公式一样，都是与路面有关的参数。路面摩擦系数与车轮滑移率的关系如图7-9所示。

由图7-9可推导出两个直线方程来表达轮胎模型，即

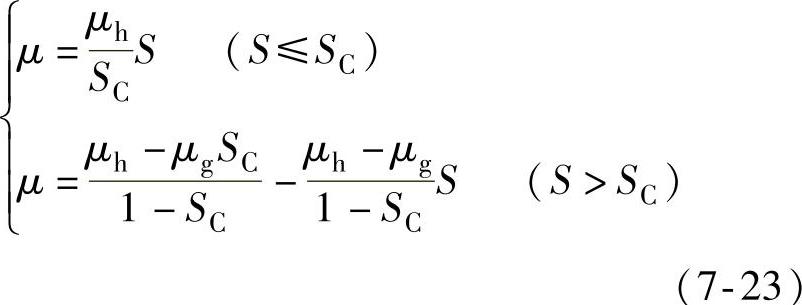
式中，μ为附着系数；μ_h为峰值附着系数；S_C为最佳滑移率；S为车轮滑移率；μ_g为滑移率100%时的附着系数。该公式体现轮胎力特性，提炼双线性轮胎模型表达式为

定义滑移率为

式中，ω为车轮角速度。此模型体现轮胎力特性趋势，而且更为简洁，适用于电动车辆BERS动力学控制领域的分析和预测。

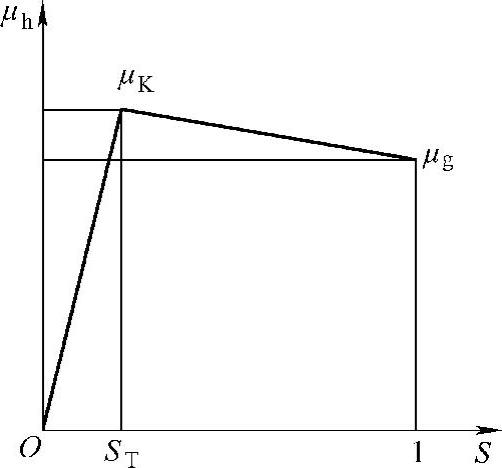
图7-9 路面摩擦系数与车轮滑移率的关系