在典型的液压制动系统中，主要的动态构件是BERS和制动管路。BERS的原理：通过与BERS前腔相连的发动机的进气管，使BERS的前腔与后腔产生一定的真空度。在制动过程中，真空阀关闭，大气阀打开，空气由大气阀进入后腔，使前腔与后腔的真空度不同，从而产生压力。在研究中发现，产生在主泵出口的制动管路压力，对迅速施加的踏板力的响应表现出明显的滞后，即此部分对于制动系统的响应滞后有较大影响。制动管路的响应迟滞与液流横截面积、制动管路的长度、管路的布置形状、制动液的可压缩性等因素有关。其基本公式为：

式中，k_L为弹性模量；V_L为管路中液体体积；Q为制动主缸制动液流量；Q′为制动轮缸制动液流量。

BERS制动器件布置如图6-10a所示，逻辑结构如图6-10b所示。为了体现系统的动态特性，踏板力输入为气缸阶跃输入，模拟紧急制动工况。轿车正常工作时BERS真空度为0.8bar，同时为了考察BERS部分失效及完全失效时液压系统的动态响应，把真空度分别确定为0.8bar、0.6bar、0bar三种。磁带机记录10个压力传感器的信号和一个踏板力传感器信号。

图6-10 实验总体布局

a）布置 b）逻辑结构

BERS结构紧凑，质量小，制动平稳，涉水性能及散热性能优良。在制动过程中，当进入压力稳定阶段后，可认为制动压力与力矩呈线性关系：

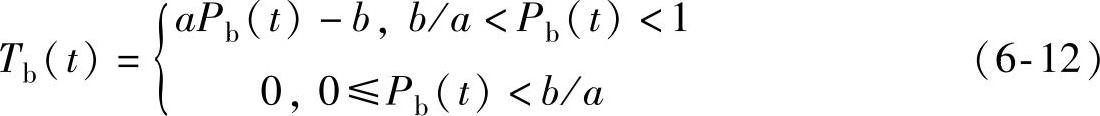
为评价BERS动态经验模型的精确性，需要把模型的输出力矩与实验测量的实际制动力矩进行比较，二者的平均误差T_error可用下式定义：

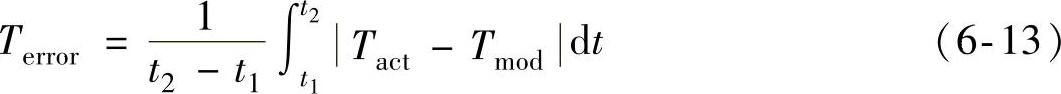
式中，T_mod为模型输出力矩；T_act为实际测得的力矩；t₁与t₂分别为测量的起始时刻与终止时刻。使用数值积分法计算力矩平均误差T_error。T_error的数值反映了计算模型与实际情况的符合程度，T_error的数值越小，模型越精确。假定制动力矩的迟滞现象仅在升压过程中存在，并可用指数时间函数来近似，那么滞后系数可表示为：

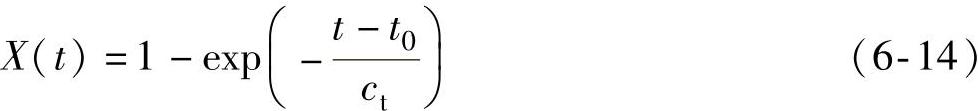
式中，t₀为制动压力上升的起始时刻；c_t为迟滞因子的时间系数。

升压过程的制动力矩存在饱和特性。根据有关标准，制动压力最高可达16MPa。由此计算，盘式BERS的许用最大制动力矩为

当制动压力下降时，记录并存储制动力矩所能达到的最小值T_min，作为下一次升压过程中制动力矩的暂存下限，则升压过程的制动力矩表示为

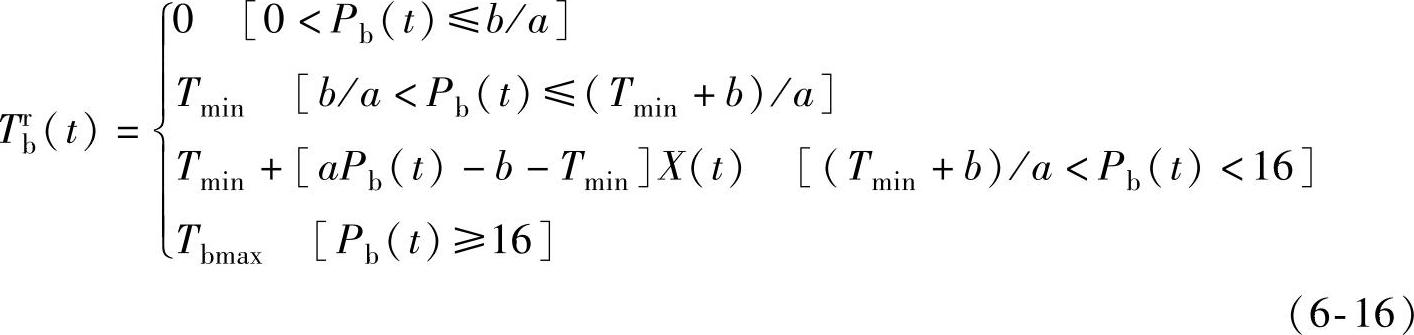
式中，a为回滞因子；b为滞环因子，T_min是升压前降压达到的力矩最小值，即升压开始时刻的制动力矩数值；X（t）是由式（6-14）确定的滞后系数。为了按式（6-16）计算升压制动力矩，需首先确定式（6-14）中迟滞因子c_t的数值。c_t的大小决定了滞后程度，对模型的精确性有重要影响。滞后系数X（t）的数学意义为时间参数t和迟滞因子c_t的二元函数，用雅可比近似法寻找c_t的最优值，使优化的目标为误差最小，目标函数是式（6-13）的变形，可表示为

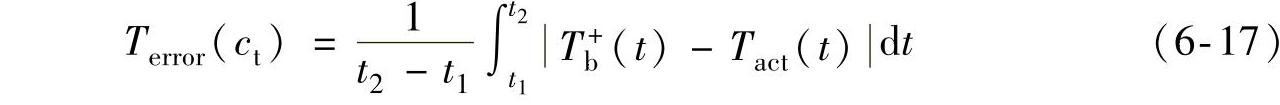
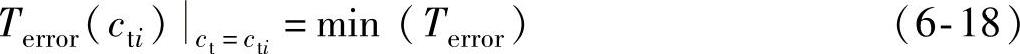(www.daowen.com)

对于一次已知的升压过程，式（6-17）是以c_t为自变量的一元函数，T_b⁺由式（6-15）计算，其他参数的定义同式（6-13）。选取一次典型的防抱死制动过程来优化计算c_t的值。根据线性拟合，可得c_t与初始制动力矩T_min之间的关系的经验公式：

c_t=-0.1048T_min+0.0378（6-19）

当T_min>0.0378/0.1048时，时间常数为零，此时制动力矩的迟滞现象基本消失，迟滞系数X（t）=1。由于受制动元件的弹性及其他多种因素的影响，降压过程中的压力-力矩关系不同于式（6-16）的线性函数。可将降压过程中的压力-力矩响应描述为可变线性模型：

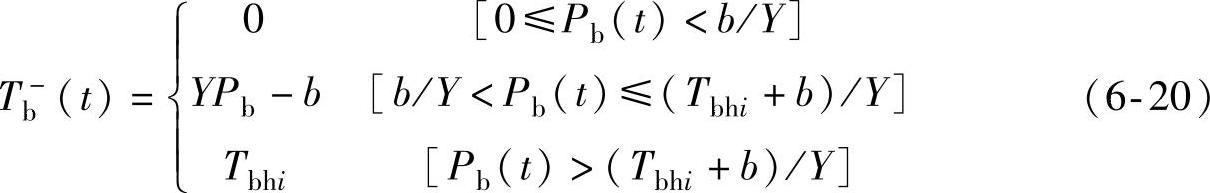
式中，T_bhi为制动压力上升时刻，制动力矩多能达到的最大值，即降压初始时刻的制动力矩数值，是一次降压过程中制动力矩的上限；Y为斜率，是可变的，其数值同样可以根据误差最小原则确定。目标函数可表示为：

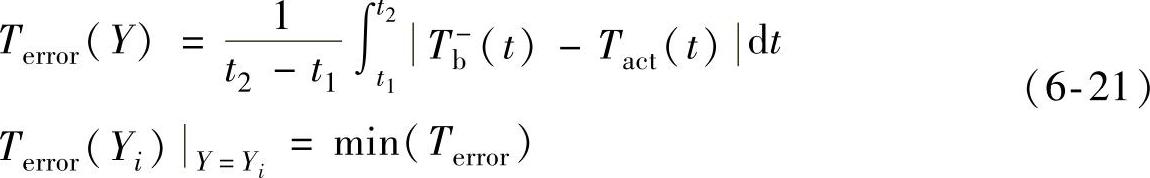
对于一次已知的降压过程，式（6-21）是以Y为自变量的一元函数，T_b^-由式（6-20）计算，其他参数的定义同上。在Y>0的约束下，求T_error（Y）极小值对应的自变量Y_i即为所求的斜率。为了减小升压过程中的迟滞效应对降压过程的影响，实验中降低了压力循环频率。制动压力循环6次，对于2～6次循环，记录升压过程制动力矩最大值。前三次实验的制动压力循环频率很高，约达到10Hz，压力-力矩响应呈现出严重的非线性与滞环。从实验结果可以得出：主缸前腔压力与后腔压力的建立相对于踏板力存在着滞后。这是由于BERS的滞后特性造成的。轮缸压力的建立相对于管路压力的建立存在着滞后，是由于管路特性造成的。在紧急制动情况下，踏板力到右后轮分泵压力延迟大约30ms，踏板力到左前轮分泵压力延迟大约12ms，踏板力到左后轮分泵压力延迟大约32ms，踏板力到右前轮分泵压力延迟大约10ms。时间延迟长短主要与管路长短有关。将ABS液压系统实验辨识出的液压系统参数代入到上述方程，仿真中用到的系统模型为

式中，p_w为轮缸内液体压力；p_r为低压蓄能器内压力；p_m为制动主缸压力或高压蓄能器压力，为12MPa。

在研究中发现，产生在主泵出口的制动管路压力，对迅速施加的踏板力的响应表现出明显的滞后，即此部分对于制动系统的响应滞后产生较大影响，如图6-11所示。制动管路的响应迟滞与液流横截面积、制动管路的长度、管路的布置形状、制动液的可压缩性等因素有关。在不同真空度下，用磁带机同时记录制动系统的输入、主缸压力、管路压力及轮缸压力的时间建立过程，即可得到液压部分的压力传递动态特性。

图6-11 BERS迟滞模型测量装置

把真空度分别确定为0.8bar、0.6bar、0bar三种。踏板力输入模拟紧急制动、缓慢制动和点制动三种情况。磁带机记录10个压力传感器的信号和一个踏板力传感器信号。不同输入、不同真空度下轿车制动系统液压管路压力、轮缸压力、主缸压力随时间建立的过程曲线如下：

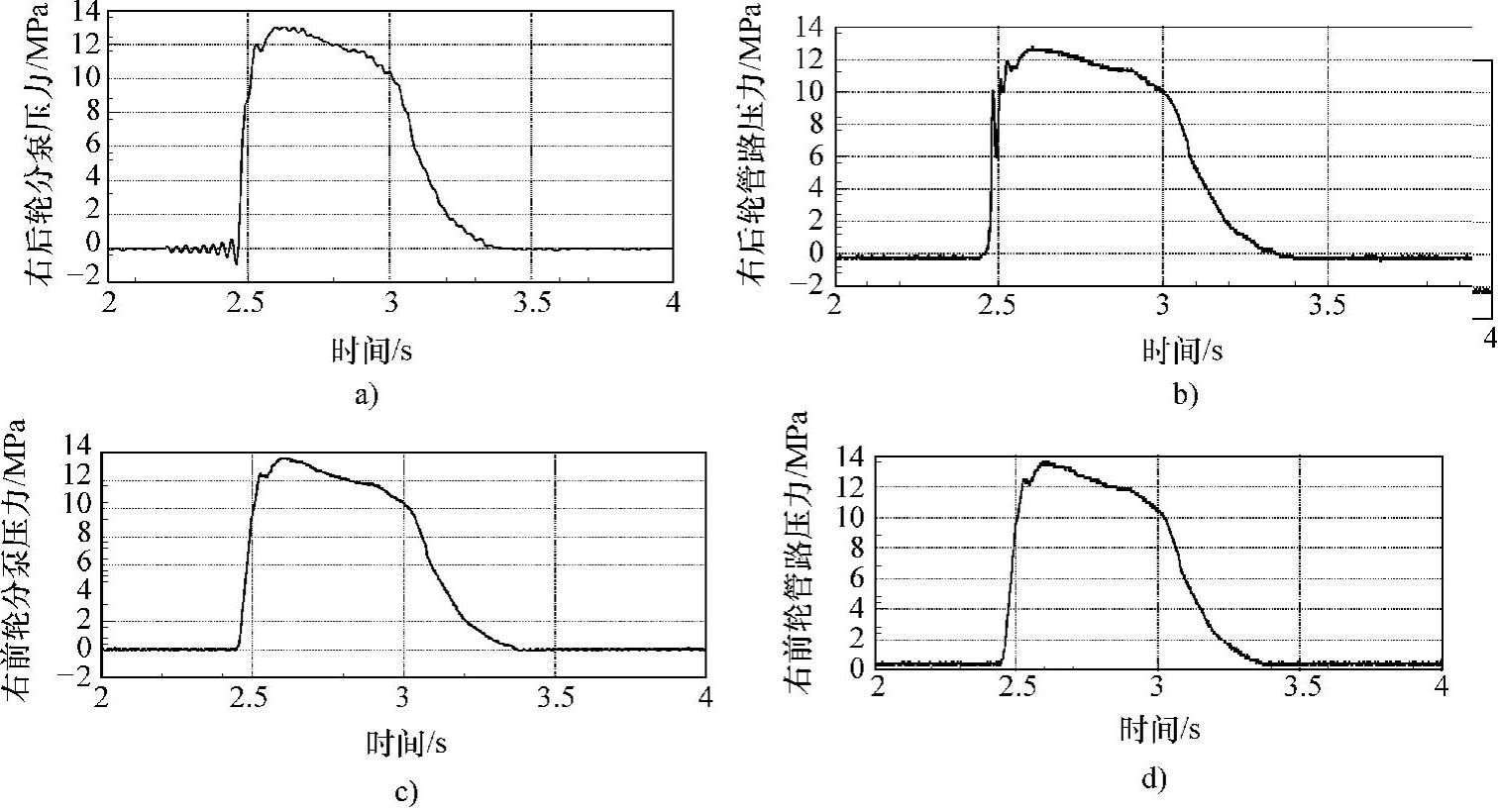
图6-12 人力输入：真空度0bar，紧急制动

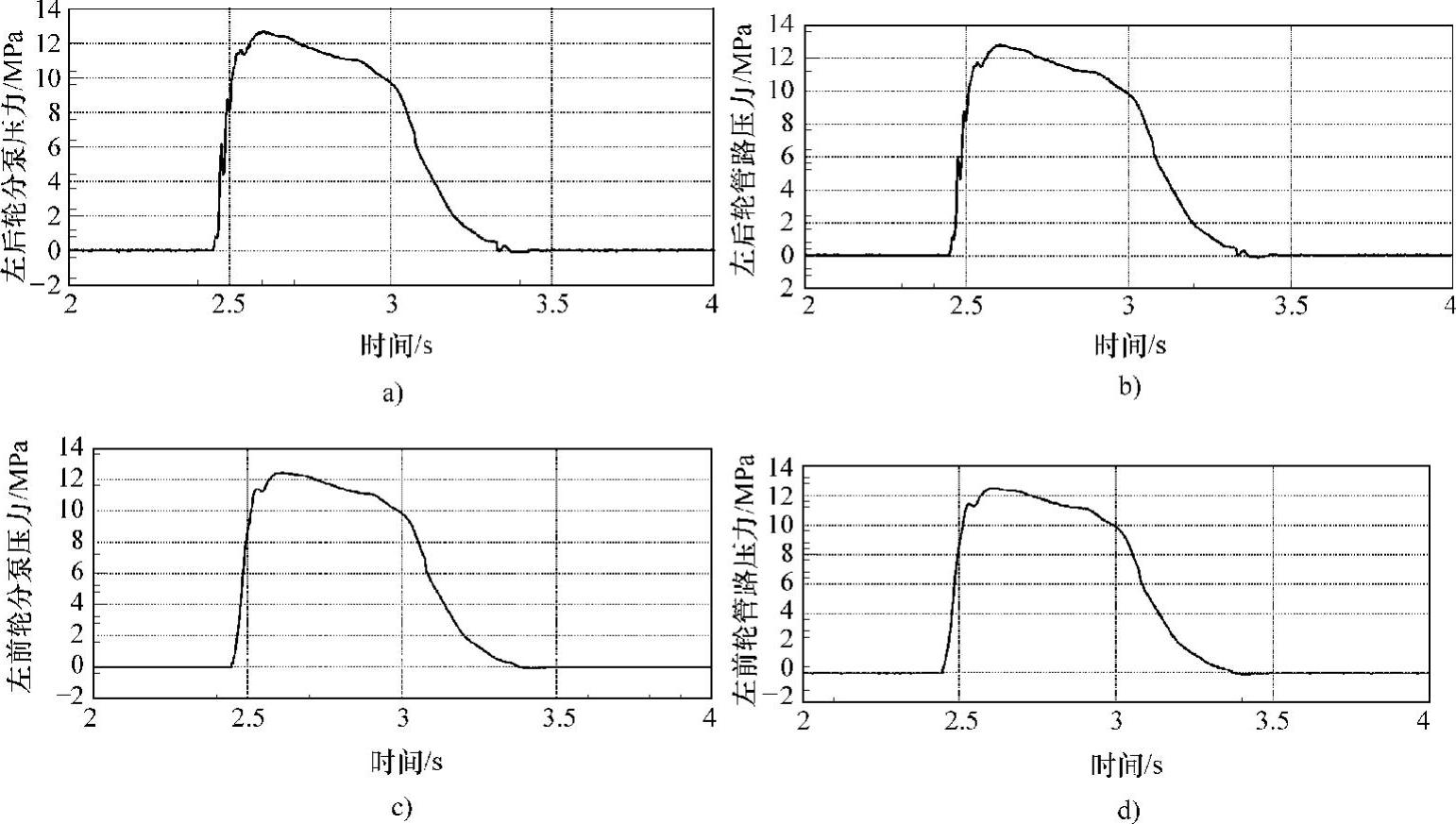
图6-13 人力输入：真空度0.6bar，紧急制动

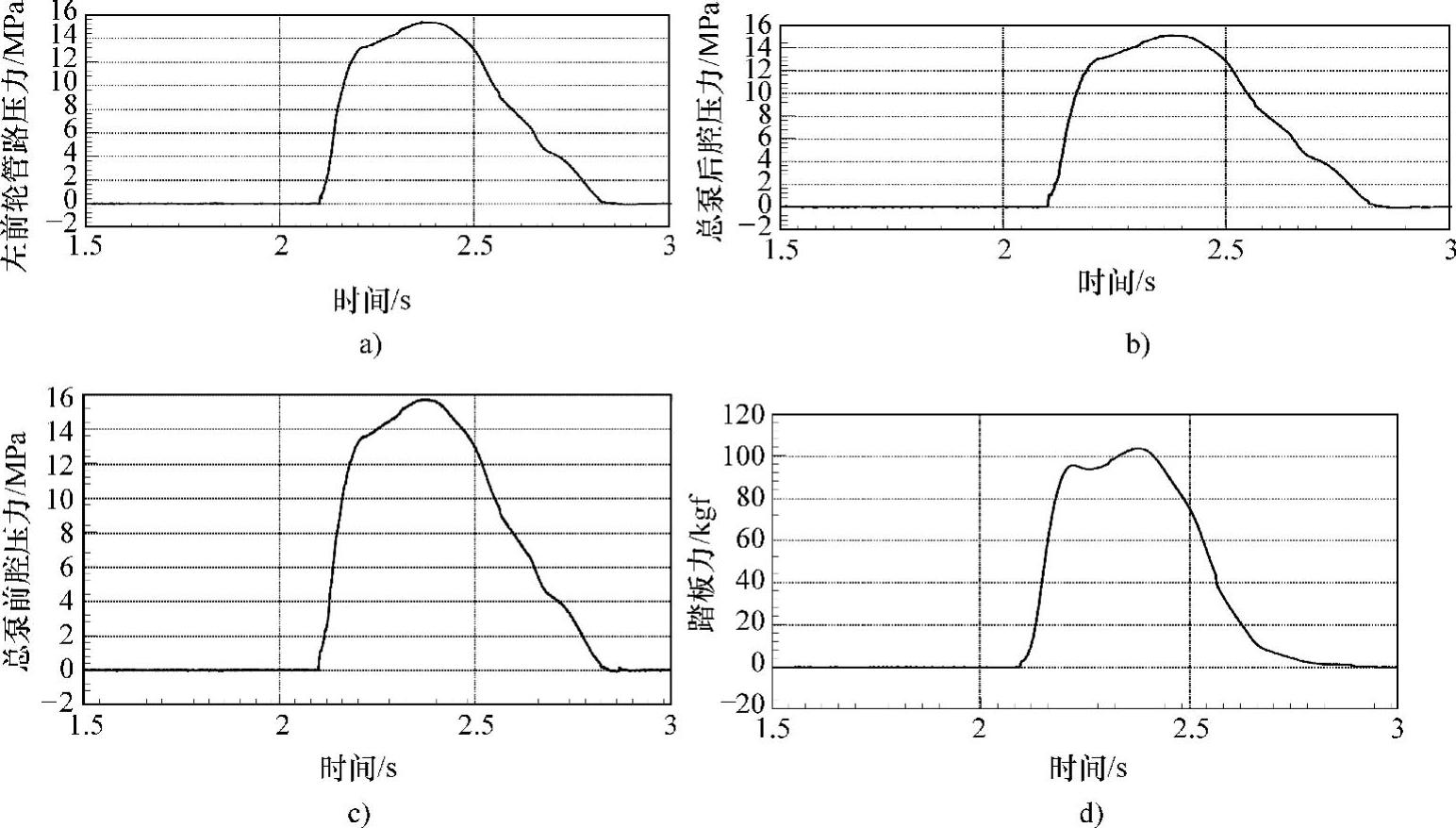
图6-14 人力输入：真空度0.8bar，紧急制动