制动液流经电磁阀阀腔时因动量发生变化会引起液动力。电磁阀阀腔流场动态响应分析中，利用流体动量原理，将制动液视为不可压缩牛顿流体，用断面平均流速和阀腔进出口压差计算单位时间内经过流断面的制动液动量。选择阀腔进出口过流断面及阀腔内壁面为控制面的控制体。制动液在单位时间内流经控制体进、出口过流断面时，由于流速方向及大小发生变化会引起稳态液动力。在阀芯开启及关闭过程中，或电磁阀进出口制动液压差出现变化时，控制体内制动液速度将随时间变化而产生瞬态液动力。本章以减压阀为分析对象，建立减压阀内制动液的湍流模型，建立阀芯所受液动力与阀芯位置和流速、进出口压差的关系。稳态液动力可用式（5-5）表示：

式中，β表示动量修正系数；C_d表示流量系数；C_v表示速度系数；b表示阀口通流截面周长；x表示阀芯的开启量；Δp表示阀芯前后压力差；θ表示制动液流经阀口时流动方向与阀芯轴线之间的角度。

由式（5-5）可知，当β、C_d、C_v、b和θ为定值时，F_稳与阀芯开启量x和阀口前后压力差Δp有关。只要阀芯有一开启量x，经过阀口的液流就会在阀芯上作用一个稳态液动力，而且不管制动液流经阀口是流入还是流出，阀芯上所受的稳态轴向液动力都是与阀芯开启量x成正比，并使阀的开口趋于减小。

因此，稳态液动力对于阀芯的作用相当于阀芯一端的回位弹簧效应。但是这种回位弹簧效应中的弹性刚度不是常量，而是随Δp变化的一个随变参量。如果在分析中Δp的变化较小，其影响可以忽略不计，则可将Δp看成是常量，这样稳态液动力就是常量，可以合并到原有回位弹簧的作用中去。对于液压电磁制动系统减压阀的回位弹簧力就是使阀芯关小的，稳态液动力相当于使原有回位弹簧的刚度k值增大。瞬态液动力可用式（5-6）表示：

式中，l表示控制体积中的有效液流长度；ρ表示制动液密度；Q表示通过阀口的流量；其表达式为：

式中，C_d表示流量系数；b表示阀口通流截面周长。从以上二式可以看出，当ρ、l、C_d、b为定值时，瞬态液动力是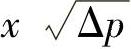的导数的函数，与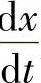成正比，即与阀芯运动速度v成正比。如果阀口前后的压力差Δp变化不大，其影响可以忽略时，可将Δp看成常量，则F_瞬亦为常量。在建立电磁阀阀腔制动液流体数学模型时，将瞬态液动力看作阻尼项。当制动液从阀口流出时，阀芯上所受的瞬态液动力与阀芯的移动速度方向相反，起阻止阀芯移动的作用，相当于正阻尼。当制动液经阀口流入时，阀芯上所受的瞬态液动力与阀芯的移动速度方向相同，起促进阀芯移动的作用，相当于负阻尼。对于减压阀来说，制动液只能在减压阀阀腔里作单向流动，即只能经阀口流出，阀芯上所受的瞬态液动力在减压阀开启过程起阻止阀芯移动的作用，在减压阀关闭过程则起促进阀芯移动的作用。选择模型控制体的时候，应将问题的边界设在条件已知的地方，如果并不知道精确的边界条件而必须做出假定时，就不要将分析的边界设在靠近感兴趣的区域，也不要将边界设在求解变量变化梯度大的地方。分析开始时还不能肯定电磁阀阀口中哪个地方梯度变化比较大，这就要先作一个试探性分析，然后根据结果来修改分析区域。阀芯附近所在的阀腔是本章要着重分析的区域，也是制动液速度、压力梯度变化较大的区域，因此模型控制体应包含这个区域。试分析后选择如图5-11所示的控制体。

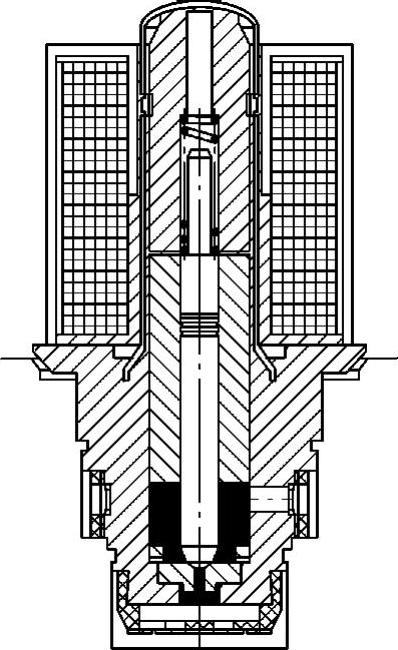
图5-11 电磁阀阀腔控制体

如果流体的密度在流动过程中保持不变或者当流体压缩时只消耗很少的能量，该流体就可以认为是不可压缩的，不可压缩流的温度方程忽略了流体动能的变化和黏性耗散。在本分析当中，制动液压力的变化所引起的流体密度变化很小，把它看作是不可压缩流。流动可以分为内流和外流，对于内流，除了进口和出口边界外，流动被壁面和对称面约束，减压阀阀腔内的制动液就是典型的内流，除了进口和出口边界，制动液处于阀体、动铁和推杆的壁面以及轴对称面的约束之中。在分析计算中，进口处速度和出口处的压力都规定为均一值，这与实际流场有差别。为减少这些假设对流场分布的影响，人为加大了出口的长度（虚拟长度），以使得真正出口处的速度具有较一致的分布。此外，对于湍流分析，回流区可能已经延伸到出口边界之后，为了使流场在出口之前可以得到充分发展，也应该加长出口后端，如图5-12和图5-13所示。

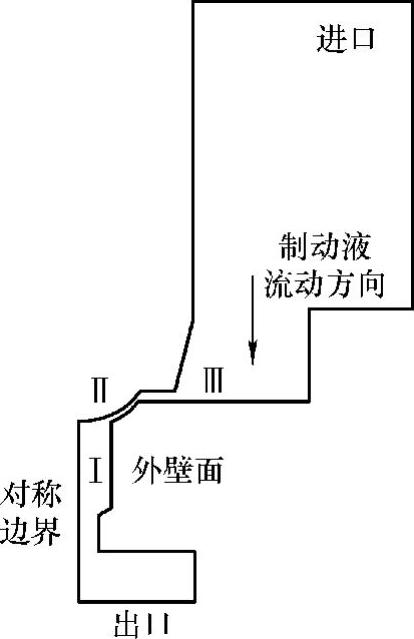
图5-12 阀腔分析区域及边界

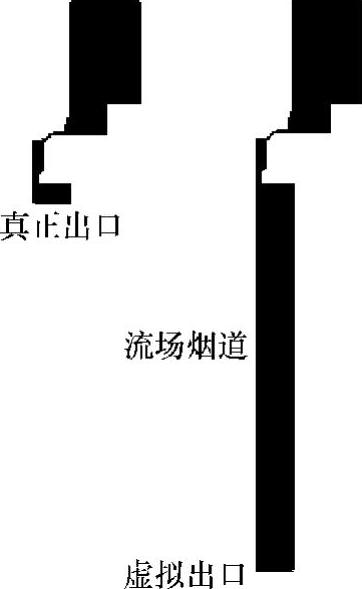
图5-13 出口虚拟长度

流场中区域Ⅰ、Ⅱ、Ⅲ处（图5-12）的流体梯度变化大，在这些地方网格作了相应的调整：在压力、速度变化梯度大的边界以及狭窄处加大单元密度，而在远离节流孔的出口处，采用大网格单元。由于使用了湍流模型，靠近壁面的区域的网格密度就比采用层流模型密得多，否则如果壁面区域的网格太粗，该网格就不能在求解中准确反映出由于变化很大的梯度对流动造成的显著影响，而在那些长边和低梯度方向一致的单元（如进口和虚拟出口区域）可以有很大的长宽比。合理调节各线的分段数、比率，保证合适的单元长宽比（在梯度变化大的区域要小，在梯度变化不大甚至没有变化的区域则可以较大），并使得单元内角在合适的范围内（25°＜角度＜155°），同时使网格密度大的区域逐步向网格密度低的区域过渡，以避免相邻单元尺寸变化过大，提高数值的稳定性。使用映射网格划分，它可以在边界上更好地保持恒定的网格特性，从而得到更精确的结果。阀芯位置改变后，必须重新划分网格。网格划分如图5-14所示，图5-14a是包括虚拟出口的整个流场有限元网格，图5-14b是不包括虚拟出口的流场有限元网格放大图，图5-14c是节流孔处流场有限元网格的局部放大图。(www.daowen.com)

流场控制方程的自由度包括流速、压力等场量。通过ANSYS后处理程序，在节点自由度计算结果的基础上，以向量图和路径图等可视化形式将节点的速度、压力等表示出来，计算阀芯所受液动力与阀芯开度、进口流速、压力等的关系。下面以阀芯开度50%时候为例分析求解结果。图5-15所示为阀口附近的有限元节点流速矢量图。在制动液流过阀口后，速度急剧上升，并且制动液的流动在阀口后端湍流发展得更明显。在阀芯开度为50%时，沿流动方向流速分量V_y等势图如图5-16所示（由左至右依次放大），图中速度V_y向上为正方向。流动通过真正的出口边界仍继续发展。在阀芯开度大于18%时，制动液沿流动方向流速分量V_y和流速V在节流孔区域Ⅱ迅速增加，在经过区域Ⅰ之后的倒角再一次节流之后，速度上升到最大值，由图5-17沿流动方向流速分量V_y等势图也可以看到V_y在区域Ⅰ处和出口处的壁面出现了回流。

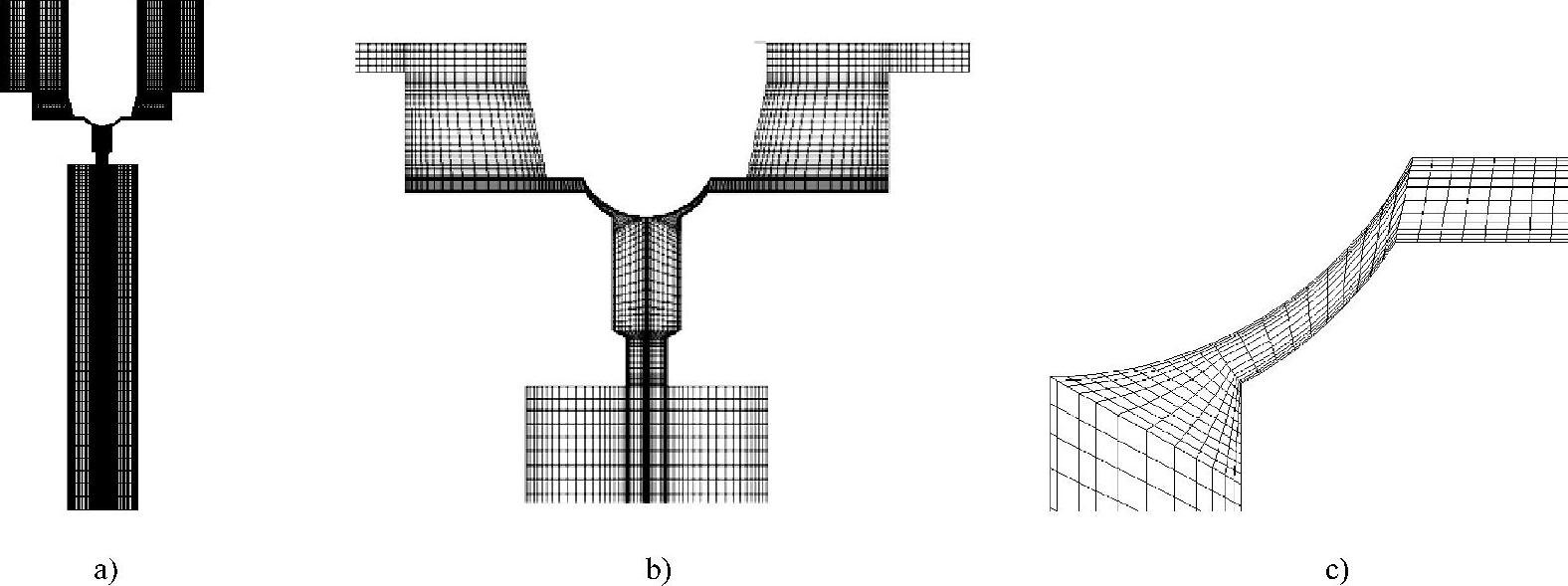
图5-14 分析区域单元划分和局部放大图

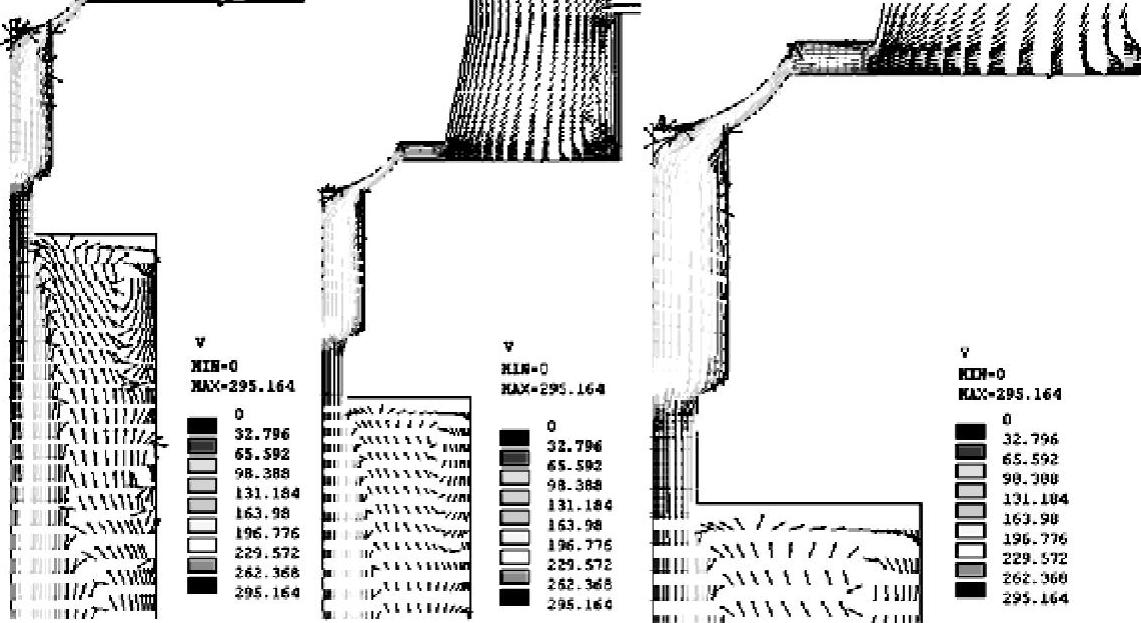
图5-15 流速V矢量图（由左至右依次放大）

阀腔压力等势图如图5-18所示（由左至右依次放大），在50%开度的时候，阀口附近区域的压力梯度已经不明显。计算结果显示，在阀芯开度大于18%时，阀芯开度变化对阀口附近区域的压力梯度已经不构成明显影响。图中的压力负值表明该处压力低于虚拟出口处的参考压力零。

图5-19由左至右分别为50%阀芯开度下的垂直于流动方向的速度分量V_x、沿着流动方向的速度分量V_y和合速度V流线分布图。在阀口后和出口处已经捕捉到了回流区，尤其在出口处的回流区已经发展得很明显。

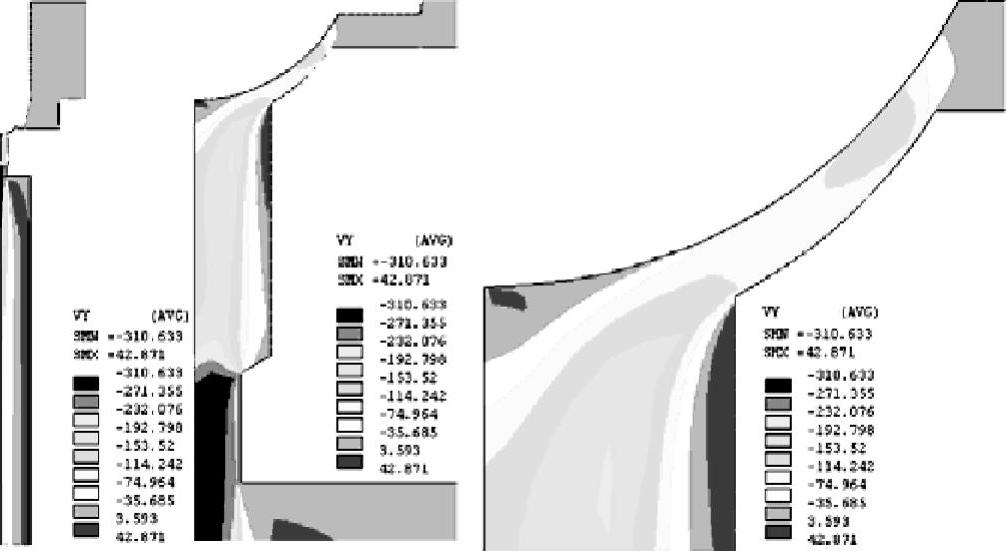
图5-16 沿流动方向流速分量V_y等势图（由左至右依次放大）

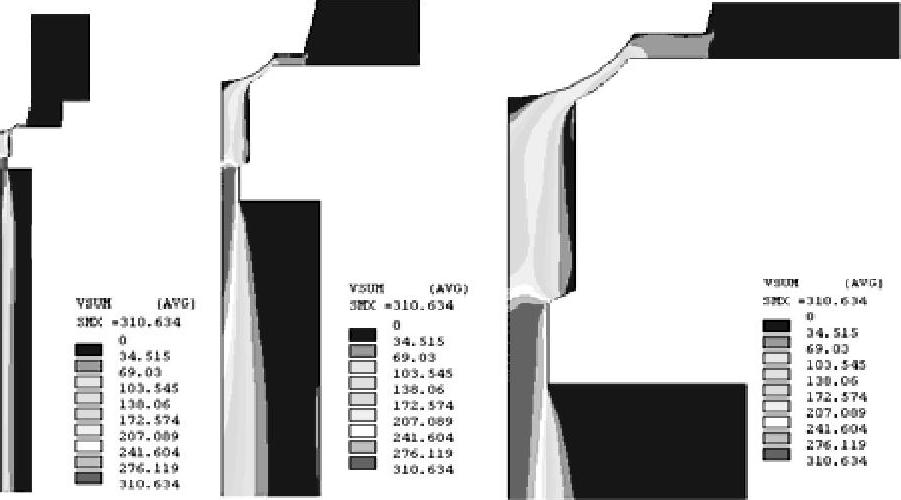
图5-17 流速V等势图（由左至右依次放大）

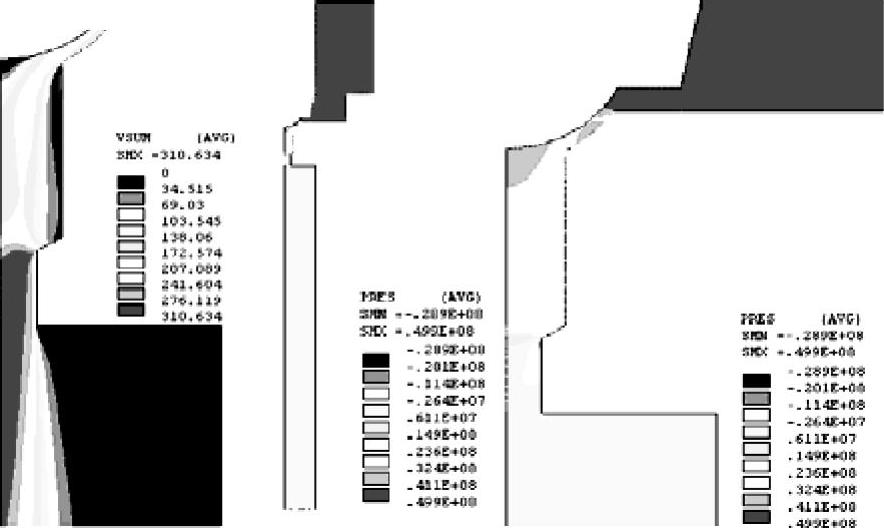
图5-18 阀腔压力等势图（由左至右依次放大）

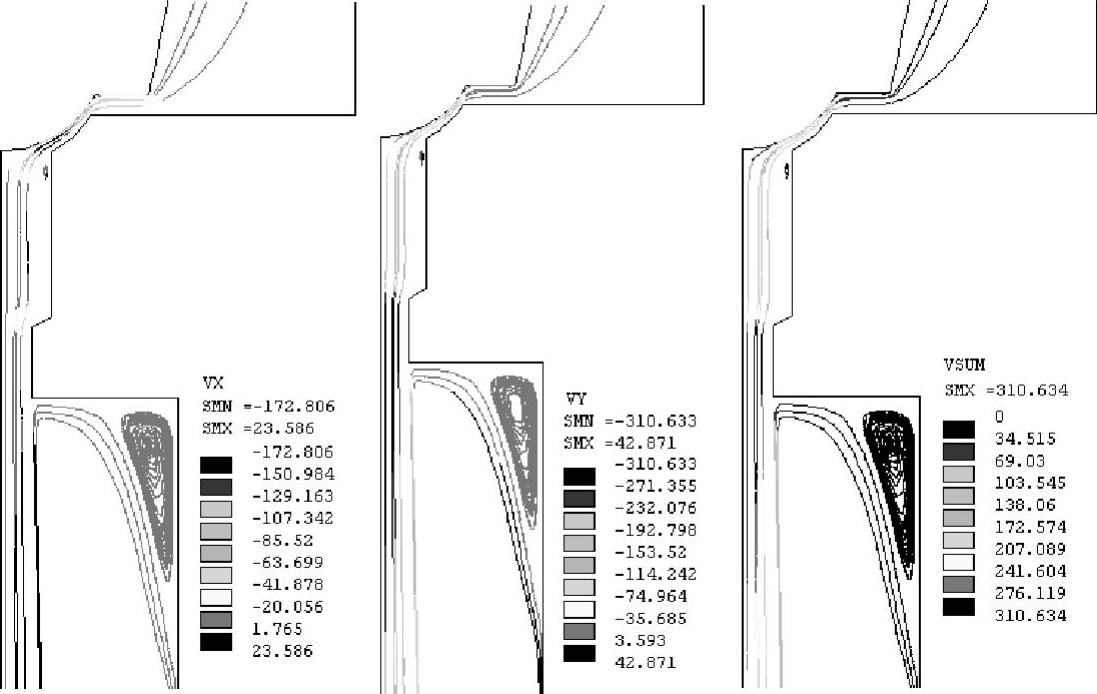
图5-19 速度流线分布图（由左至右为V_x、V_y、V）