所谓评价信息的集结,是指在综合评价中,运用一定的数学模型(或称综合评价函数、集结算子),将多个评价指标值转换或合成为一个整体性的综合评价值,并依此进行决策。可用于“合成”的数学函数和方法较多,关键在于我们如何根据评价目的及评价系统的特点,选择较为合适的集结算子。[56]
目前,已有的信息集结方法主要有线性加权综合法、非线性加权综合法、增益型线性加权综合法、理想点法(类似的有密切值法)、有序加权平均算子(OWA)、有序加权几何平均算子(OWGA) 及其扩展的集结算子、密度中间(DM) 算子,还有基于“不确定”或“模糊语言”等环境下的信息集结方法[57]等,其中前两种方法因其计算简便和直观意义明显而最为常用。然而这些方法主要是用来处理静态的综合评价问题,目前对动态评价系统的集结方法研究还很少。只有郭亚军等(2007) 进行了积极探索,将OWA 算子及相关算子推广到时序数据集结中,提出了时序加权平均(time ordered weighted averaging,TOWA) 算子和时序几何平均 (time ordered weighted geometric averaging,TOWGA) 算子,并将之应用于动态综合评价问题。但通过文献我们不难发现,这两种算子各具特点,在数据集结中各有利弊,运用不同的单一算子集结模型对相同决策对象进行动态评价时,会出现不同甚至有时相悖的评价结论,仍然有待进一步完善。因此,本节在简要介绍时序集结算子相关理论的基础上,提出了一种新的混合时序算子集结方法,构建了基于组合TOWA 算子和TOWGA 算子的动态多指标评价模型,并合理的确定集结模型中比例参数,运用这一集结算子对动态综合评价问题进行实证应用。结果表明该模型既充分考虑时间权向量,又能有效克服单一算子集结模型的弊端,所得结果更具稳定性,有助于我们得到更为合理的评价结果,促进科学决策。
6.1.4.1 时序集结算子
美国著名学者Yager (1988) 提出了OWA 算子,随后该算子在管理决策、模糊系统、图像压缩等多个领域得到了广泛应用。[58]接着Yager (1999)将其推广,提出了诱导有序加权平均(IOWA) 算子。之后,Chiclana F. 等(2001) 提出了有序加权几何平均(OWGA) 算子,Yager (2004) 提出了一种连续区间数据的OWA (即C-OWA) 算子,Chen H.Y. 等(2005) 又提出了诱导有序加权几何平均(IOWGA) 算子。徐泽水(2005) 进行了拓展研究,提出了加权的C-OWA (WC-OWA) 算子、有序加权的C-OWA(OWC-OWA) 算子以及组合的C-OWA (CC-OWA) 算子,并研究了这些算子的性质和应用。Yager 等(2006) 提出了连续区间数据有序加权几何平均(C-OWGA) 算子,从而可以实现连续性区间数据信息的集成,但却无法进行多个区间数据信息的集成。随后,王坚强等(2007) 针对准则值为正态分布随机变量、其他参数不确定的随机多准则决策问题,提出了WCOWA 算子。龚艳冰等(2008) 将C-OWA 算子扩展到模糊环境,提出了一些模糊C-OWA (FC-OWA) 算子。但是以上这些算子都没有考虑时序的影响,主要用来处理静态的多指标决策问题。郭亚军等 (2007) 提出了TOWA 算子和TOWGA 算子,这为处理带有时序的动态综合评价问题提供了新的数据集结方法。下面将简要介绍相关定义[59]:
定义6.1 (TOWA 算子) 设N = {1,2,…,n} ,tj 为时间诱导分量,xj 为数据分量,称〈tj,xj〉 (j ∈N) 为TOWA 对。定义时序加权平均(TOWA) 算子为
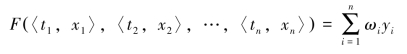
其中ω =(ω1,ω2,…,ωn)T 是与F 相关联的加权向量,ωi ∈[0,1] ,且 中第i 时刻所对应的TOWA 对中的第2 个分量,则称函数F 是n 维TOWA 算子。
中第i 时刻所对应的TOWA 对中的第2 个分量,则称函数F 是n 维TOWA 算子。
定义6.2 (TOWGA 算子) 设N = {1,2,…,n} ,tj 为时间诱导分量,xj 为数据分量,称〈tj,xj〉 (j ∈N) 为TOWGA 对。定义时序几何平均(TOWGA) 算子为

其中ω =(ω1,ω2,…,ωn)T 是与G 相关联的加权向量,ωi ∈[0,1] ,且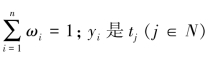 中第i 时刻所对应的TOWGA 对中的第2 个分量,则称函数G 是n 维TOWGA 算子。
中第i 时刻所对应的TOWGA 对中的第2 个分量,则称函数G 是n 维TOWGA 算子。
TOWA 和TOWGA 算子的实质是:将时间诱导分量tj (j ∈N) 按某一时间顺序排序后所对应的数据分量(x1,x2,…,xn) 进行加权集成,ωi 与元素xi 的大小和位置无关,只与时间诱导分量顺序的第i 个位置有关。
6.1.4.2 基于CTOWA 算子的动态混合集结模型
从定义6.1 和定义6.2 易知,TOWA 算子和TOWGA 算子分别是“和性”的与“积性”的,因此两种算子在数据集结过程中的侧重点各不相同。TOWA 算子突出了系统发展过程的功能性,即允许评价对象各时间样本点处的评价值有较强的互补性; TOWGA 算子突出了系统发展过程的协调性,即强调评价对象各时间样本点发展的均衡性。[60]TOWA 与TOWGA 算子在数据集结上各有利弊,因此将两种算子组合成同时兼顾功能性与均衡性的集结模型将更为合理,得到的评价结果将更加贴近实际且更易于被人们接受。
设动态多指标评价问题的指标集为u={u1,u2,…,um} ,评价方案集为o = {o1,o2,…,on} ,共有l 个时间样本点集t = {t1,t2,…,tl} ,评价方案ok 对应于时间样本点tj 、指标ui 的原始统计数值序列为{xik(tj)} ,规范化预处理后的指标值序列记为{yik(tj)} ,其中i = 1,2,…,m,k =1,2,…,n,j = 1,2,…,l。为了突出在不同时期不同指标重要性的差异,对于评价方案集中的任意一个元素ok ( k = 1,2,…,n),第i 个评价指标在tj 时段记为uij ,其权数记为ωij ,即对每一方案ok ( k = 1,2,…,n),在tj 时段指标集的权向量为ωj =(ω1j,ω2j,…,ωmj)T( j=1,2,…,l)。因此,在属性集u、时间样本点集t 下,该动态多指标评价问题的指标权向量为ω = (ω1,ω2,…,ωl) ,并记时间样本点集t 的权向量为ξ =(ξ1,ξ2,…,ξl)T 。
根据评价方案ok 对应于时间样本点tj 、指标ui 的规范化预处理后的指标值序列{yik(tj)} ,以及评价指标ui 在tj 时段的权系数ωij (其中i = 1,2,…,m,k = 1,2,…,n,j = 1,2,…,l),由选定的综合评价模型可以求出离散方案ok 在时段tj 处的集结值vk(tj) ,其中

此处zik(tj) 可以取yik(tj) ,也可以采用理想矩阵法或模糊优选法或灰关联分析法等方法将yik(tj) 处理后所得的结果。
为了体现时序对评价系统的影响,引入TOWA 和TOWGA 算子分别计算方案ok 在时间样本点集t = {t1,t2,…,tl} 上的集结值为
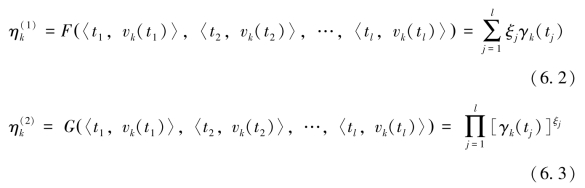
式中, 和
和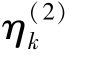 分别表示TOWA、TOWGA 算子集结值,γk(tj) 表示时间样 本 点 集 中 tj 所 对 应 的 TOWA 或 TOWGA 对 中 的 vk(tj) ,ξ =(ξ1,ξ2,…,ξl)T 表示系统的时间权向量。
分别表示TOWA、TOWGA 算子集结值,γk(tj) 表示时间样 本 点 集 中 tj 所 对 应 的 TOWA 或 TOWGA 对 中 的 vk(tj) ,ξ =(ξ1,ξ2,…,ξl)T 表示系统的时间权向量。
可见,TOWA 算子和TOWGA 算子分别突出系统发展过程的功能性和均衡性,而在实际问题中,很多系统的运行状况本身就是功能性与均衡性这二者的有机统一,因此为了更加合理贴切的阐述问题,我们将这两种时序算子进行组合,构建兼顾功能性与均衡性的动态混合集结模型,提出了组合时序加权平均(CTOWA) 算子。下面给出其定义和性质:
定义6.3 (CTOWA 算子) 设CTOWA:Rn →R,若
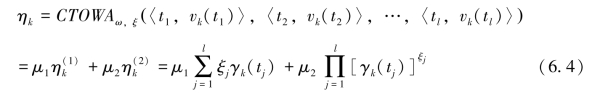
其中,![]() 是与函数CTOWA 相关联的加权向量,ξj ∈
是与函数CTOWA 相关联的加权向量,ξj ∈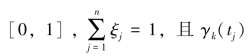 表示时间样本点集中tj 所对应的TOWA 或TOWGA 对中的第2 个分量vk(tj) ,而集结值vk(tj) 由(6.1) 式确定:vk(tj)
表示时间样本点集中tj 所对应的TOWA 或TOWGA 对中的第2 个分量vk(tj) ,而集结值vk(tj) 由(6.1) 式确定:vk(tj) 可取指标规范化预处理值yik(tj) 或者其他综合评价方法对yik(tj) 的处理值],ω=(ω1,ω2,…,ωl) 表示指标权向量,μ1、μ2 分别为TOWA 算子和TOWGA 算子的比例系数,满足μ1 ≥0,μ2 ≥0,μ1 +μ2 = 1,则称函数CTOWA 是组合时序加权平均算子,也称CTOWA算子。
可取指标规范化预处理值yik(tj) 或者其他综合评价方法对yik(tj) 的处理值],ω=(ω1,ω2,…,ωl) 表示指标权向量,μ1、μ2 分别为TOWA 算子和TOWGA 算子的比例系数,满足μ1 ≥0,μ2 ≥0,μ1 +μ2 = 1,则称函数CTOWA 是组合时序加权平均算子,也称CTOWA算子。
CTOWA 算子的特点是:对第一次加权计算得出的评价数据对向量(〈t1,vk(t1)〉,〈t2,vk(t2)〉,…,〈tl,vk(tl)〉) ,按某一时间顺序排序后所对应的数据分量(vk(t1),vk(t2),…,vk(tl)) ,分别进行第二次TOWA和TOWGA 算子加权后线性集成,ξj 与元素vk(tj) 的大小和位置无关,只与时间诱导分量顺序的第j 个位置有关。比例系数μ1、μ2 分别表示时序算子TOWA 和TOWGA 在动态评价系统中的相对重要程度,在实际应用中可根据不同问题的特点和需要合理确定其取值。(https://www.daowen.com)

即此时的CTOWA 算子即为TOWGA 算子。
可见,CTOWA 算子同时推广了TOWA 算子和TOWGA 算子,它不仅考虑了系统发展过程的功能性,而且还体现了系统发展过程的均衡性。因此,在实际应用中该算子能更好地反映现实情况。不难证明,CTOWA 算子还具有以下性质:
定理6.1 (单调性) 设任意两个时序数据对向量

![]() 是任一时序数据对向量,若对
是任一时序数据对向量,若对![]() 都有vk(tj)= ak ,则
都有vk(tj)= ak ,则
![]()
定理6.3 (介值性) CTOWA 算子介于MAX 算子和MIN 算子之间,即对任意时序数据对向量
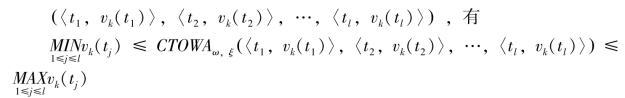
定理6.4 若ξ =(1/l,1/l,…,1/l)T ,则相应的CTOWA 算子即为算术平均算子与几何平均算子的线性组合,即

定理6.5 若ξ=(1,0,…,0)T ,则相应的CTOWA 算子值为γk(t1) ,即时间样本点t1 所对应的TOWA 和TOWGA 对中的第2 个分量vk(t1) ,表示此时只关注评价系统中的远期数据,即
![]()
定理6.6 若ξ=(0,0,…,1)T ,则相应的CTOWA 算子值为γk(tl) ,即时间样本点tl 所对应的TOWA 和TOWGA 对中的第2 个分量vk(tl) ,表示此时只关注评价系统中的近期数据,即
![]()
为了比较分析笔者所提出的CTOWA 算子与TOWA (或TOWGA) 算子的异同点,验证CTOWA 算子集结DMADM 问题的合理性和优越性,现选取郭亚军等 (2007) 的应用算例,运用CTOWA 算子对中国西部12 省市1999—2004 年的宏观经济发展状况进行动态综合分析。由于此处是为了比较集结算子之间的差异性,因此本节采用与该文献相同的数据维与时间维集结顺序、指标预处理方法和确定各时刻指标的权向量,由线性加权综合模型进行综合,得到各时刻的第一次加权评价值vk(tj) ,且时间权向量为ξ =(0.0029,0.0086,0.0255,0.0755,0.2238,0.6637)T ,利 用 TOWA(或TOWGA) 算子对第一次加权数据进行集结,求得集结值 和
和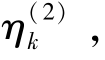 并根据
并根据 和
和 确定西部12 省市宏观经济发展状况的序关系可见该文献[61](此处略)。
确定西部12 省市宏观经济发展状况的序关系可见该文献[61](此处略)。
下面应用本书提出的组合时序加权平均(CTOWA) 算子计算中国西部12 省市6 年的宏观经济发展状况集结值。为了使集结结果更具客观性,此处取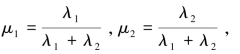 其中
其中
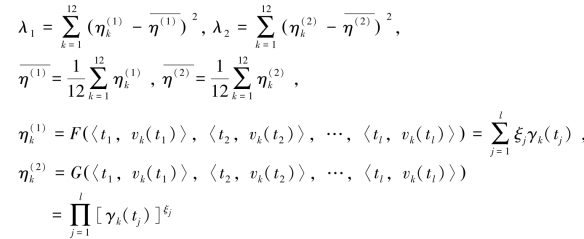
将相关数据和ξ 值代入上述公式,经计算得μ1 =0.50003,μ2 =0.49997。在此需要说明的是,此处的比例系数μ1 和μ2 取值很接近,原因正如郭亚军等(2007) 所指出的一样,西部各省市在1999—2004 年发展过程中波动不大,同时也和时间度θ 的选取有关,这也使得TOWA 和TOWGA 算子集结数值较为接近。当然确定比例系数μ1 和μ2 的方法较多,可由决策者主观赋值,也可按各点到正理想点的相对接近度等方法来确定,即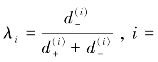 1,2,其中
1,2,其中
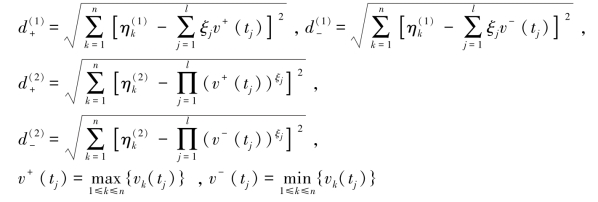
此时可算出μ1 = 0.50065,μ2 = 0.49935,显然与上述方法算得结果比较接近。在应用中决策者可根据不同的具体问题确定合理的比例系数。然后根据CTOWA 算子的定义计算可得该评价系统的综合集结值如表6-8所示。
表6-8 评价系统的CTOWA 算子集结结果

从郭亚军等(2007) 可知,西部12 省市宏观经济发展状况的TOWA 算子和TOWGA 算子的集结结果并不一致,其中重庆和陕西、青海和甘肃等省区的序关系发生了变化,出现了逆序的情况; 而从表6-8 可见,运用本书提出的CTOWA 算子对西部12 省市宏观经济发展状况进行集结时,其序关系结果(除了重庆和陕西外) 和TOWA 算子的结论完全一致,而且重庆和陕西的集结值偏差也很小。同时计算可得,这三种算子集结值的离差平方和分别为2.5084、2.5080、2.5097。因此,该算例的实证结果表明:从理论上来看,本书提出的组合时序加权平均(CTOWA) 算子在充分考虑时间权向量的基础上,不但同时兼顾了系统发展过程的功能性与均衡性,而且也能最大程度地体现出各决策方案之间的差异,有利于促进系统整体的均衡发展; 从实践上看,CTOWA 算子集结过程更具合理性和公正性,所得结果更具有稳定性,因此可为投资者或决策者提供一定的参考意义,同时该算子也可广泛应用于其他动态综合评价问题的集结和决策。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





