对多指标评价系统中权向量的判断及赋值，是专家经验和决策者意志的体现，在一定程度上决定了多指标综合评价的精度，也决定着评价决策的公正性。^[23]因此可以说，评价系统权向量的确定是多指标综合评价的核心问题，对评价有着重要意义，对此学术界进行了广泛的研究^{[24][25][26][27]}。而在带有时序的动态多指标评价系统中，诸如本章要进行的高等教育投资结构的合理性评价，就需要确定两个相关因素的权重：指标的权向量和时间的权向量。

然而，在现有研究中虽然关于动态多指标评价方法的探讨较多，但对于其中权向量的确定却研究甚少，基本采用的是静态的处理方法，甚至有些文献采用均分法或者专家直接赋值法，这显然不能满足多指标评价中动态决策的需要，也无法客观真实的反映问题。基于此，本节结合已有研究，首先探讨动态评价系统中指标权向量的确定问题，引入标准正态分布，尝试性提出了新的群组决策时序动态序关系分析法； 然后在动态评价系统中引入时间权向量，提出了一种新的最小方差规划模型来寻找一组最稳定的样本集结的时间权系数。

6.1.3.1　动态评价系统中指标权向量的确定

在多指标评价中，确定权向量的方法主要分为两类，即主观赋权法和客观赋权法。主观赋权法的源信息来自专家群的知识和经验，是决策者根据经验主观判断赋值，或根据各指标重要程度的判断计算出权系数的方法，如Delphi 法^[28]、AHP 法^[29]、最小平方和法^[30]，还有二项系数法、网络分析法（ANP）、相邻指标比较法、环比评分法等。该类方法简便易行，赋权结果相对比较合理，主要缺点是主观随意性较大，评价过程的再现性较差。客观赋权法的源信息来自实际统计数据构成的决策矩阵，是利用各指标所提供的信息，构造数学模型来确定权重系数，如因子分析法^[31]、熵值法^[32]、多目标规划法^[33]，还有最优权法、均方差法、主成分分析法、功效评分法等。该类方法客观性较强，评价过程的再现性较好，主要缺点是确定的权重多属于信息量权重，没有充分考虑指标本身的相对重要程度，有时所得结果不合常理、难以解释，甚至与决策者的愿望相违背。可见，这两类赋权方法各有利弊，因此有学者提出了将这两类赋权法进行组合集成，得到了一些有益的成果，如数学规划模型集成主客观权重^[34][35]、基于粗集理论求解综合权重^[36]、基于线性目标规划求解组合权^[37][38]、建立偏差矩阵确定组合权系数^[39]、基于熵理论综合集成权重^[40][41]、基于二元语义和最小偏差集成主客观权重^[42]等。

然而，上述方法主要是用来确定静态的多指标权重问题，而关于动态评价系统中的权向量确定却研究甚少。因此，笔者尝试将决策者群组判断和数学模型科学计算相结合的集成方法确定权向量，引入正态分布，提出了新的群组决策动态G1-法。这样既可充分利用专家群的信息源，又可利用正态分布的良好性质，削弱了主观性的影响，减少误差，使决策分析更具客观性和公正性。

G1-法即序关系分析法，是郭亚军等（1992） 在剖析特征值法求权数所存在问题的基础上，提出的一种无须一致性检验，且具有保序性的新方法。但是该方法主要用于静态多指标决策问题的处理中，于是郭亚军（1995）又将该方法推广到具有时序特征的动态情形。其中，为了减弱该方法的主观性影响，更加客观、准确的计算指标权向量，在静态的情形该方法还考虑了含有相互独立的L（L ＞1） 位决策者的群组判断问题^[43]：提出取决策者判断后所得结果的算术平均值，然后加权集成每个指标的权系数，这为人们运用群组决策序关系分析法求解权系数提供了一种有效的途径。但是在该方法中，每位决策者做出的判断被默认为具有一致的重要性，都赋予了相同的权重1/L。而事实上，在实践问题中，由于受知识水平、实践经验和决策环境等的影响，不同决策者的思维并不具有一致性，所作出的判断也存在较大的差异性，甚至在决策过程中可能还存在判断的不公正性。因此笔者认为在群组决策过程中，只是取算术平均进行线性加权具有一定局限性，它无法避免或削弱上述因素的影响。为此，笔者借鉴王煜等依决策数据赋权法的思想^[44]，引入正态分布，利用该分布的良好性质，根据不同决策者的判断数据计算其对应的权系数，然后将群组判断结果加以集成，提出了一种新的群组决策动态G1-法。下面分三种情况加以讨论：

（1） 若L（L ＞1） 个序关系完全一致

设在tj（ j=1，2，…，l） 时段，在某评价目标下，L 位决策者建立的评价指标u1j，u2j，…，umj 的序关系完全一致，即：　且决策者h 关于λij 的理性赋值记为2，…，L；j = 1，2，…，l），并满足。为了更好地评价每一个决策者赋值数据对研究问题判断的公正程度，使得集结结果更加公正和真实，在此利用N（0，1） 分布的良好性质，分别求出φ（y） 在λ（ij h）标准化处理后对应点处的函数值，即令

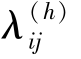其中再作单位化处理： 则表示决策者h 关于λij 的理性赋值对应的权系数，且满足0 ≤≤ 为便于后续的讨论，不妨记将其进行加权集成，可得L 位决策者的群组判断综合值，记为γij ，即

根据评价指标u1j，u2j，…，umj 之间的序关系式，调整顺序后即得对应的权数ωij 和权向量ωj =（ω1j，ω2j，…，ωmj）T （ j = 1，2，…，l） 以及ω =（ω1，ω2，…，ωl） 。

（2） 若L（L ＞1） 个序关系部分一致

不失一般性，不妨设在tj （j=1，2，…，l） 时段，在某评价目标下，对于评价指标u1j，u2j，…，umj ，有L0（1 ≤L0 ＜L）位决策者建立的序关系完全一致。此时对任一指标uij ，由上述情形（1） 可求出这L0 位决策者的集成权数ωij′ （ i = 1，2，…，m；j = 1，2，…，l）。

另一方面，设序关系不一致的L - L0 位决策者建立的序关系分别为因此

其中表示决策者h 对评价指标集 中元素按序关系“ ≻”排序后的第i（ i = 1，2，…，m） 个指标。

设在tj （j =1，2，…，l） 时段，在某评价目标下，决策者h 关于评价指标的重要性程度之比的理性赋值分别为满 足则可计算出tj 时段决策者h 关于评价指标uij 对应的权系数 记同情形（1） 一样，令

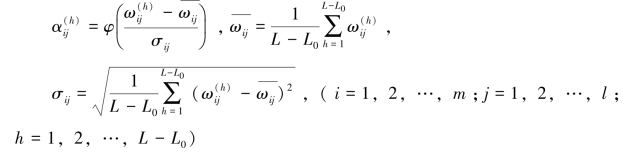
其中 并作单位化处理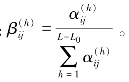：此时表示权系数值所对应的权数，不妨记将其进行加权集成，可得序关系不一致的L-L0 位决策者的群组判断集成值，记为m；j = 1，2，…，l）。

因此，在tj （j = 1，2，…，l） 时段，在某评价目标下，指标uij 对应的权数为

式中比例系数μ1，μ2 ＞0，且μ1 ＋μ2 =1。一般地，可取μ1 =L0/L，μ2= 1 - L0/L。

（3） 若L（L ＞1） 个序关系不一致

更一般的情形：设在tj （j = 1，2，…，l） 时段，在某评价目标下，L 位决策者中分别有位决策者，建立了相同的序关系，不妨设Lh 位决策者关于评价指标u1j，u2j，…，umj 建立的序关系如下：

决策者之间重要性程度之比的理性赋值分别为（ i = m，m - 1，…，3，2； j = 1，2，…，l； h =1，2，…，s；k=1，2，…，Lh ），并满足 ＞1。由上述情形（1）可得

再　作 单 位 化 处 理： 则 理 性 赋 值 向 量 对应的权向量为因此可计算得到Lh 位决策者的群组判断

根据序关系式调整顺序，即得各指标uij 所对应的权数（ i = 1，2，…，m；j =1，2，…，l；h =1，2，…，s）。最后，将Lh 种情况进行线性加权，即(www.daowen.com)

其中比例系数一般地，可取μh = Lh/L（ h = 1，2，…，s）。因此，在tj 时段，指标uij 的权向量为ωj =（ω1j，ω2j，…，ωmj）T （ j = 1，2，…，l），即在指标集u 和时间样本点集t下，该动态多指标评价系统的指标权向量为ω = （ω1，ω2，…，ωl） 。

综上所述，在探讨动态评价系统中指标权向量的确定问题时，本书尝试性提出了新的群组决策动态G1-法，不仅将静态群组决策分析法拓展到了对动态评价系统的研究，而且将群组决策的处理方法进行了更具公正性的改进。因此该方法除了具备静态序关系分析法的优点外，还具有以下良好的性质：（1） 时序因素的引入，使得该方法可以用来处理动态系统中指标权向量的确定问题，拓宽了应用范围； （2） 在确定指标权向量时，考虑了不同时期不同指标重要性的差异，使得问题的研究更具严谨性和全面性，这也更符合实际问题的客观情况； （3） 群组决策时引入正态分布，充分利用了标准正态分布的良好性质，减弱了决策者判断的主观性影响，使得集结结果更具公正性和客观性。

6.1.3.2　动态评价系统中时间权向量的确定

在动态多指标评价系统中，在不同时间样本点处，不同指标的重要性是存在差异性的，决策方案的偏向型也是不同的，因此处理时必须考虑时序的影响，科学的确定对应的时间权向量。

时间权向量能够反映不同时间样本点的相对重要程度，因此可以说，科学确定时间权向量，将对能否获得合理决策结果起着关键性作用。从目前可查阅的文献来看，这一问题虽引起了重视，但研究成果并不多见，在Filev D. 和Yager R. R. 分析了OWA 算子最大熵的性质^[45]，Fullér R. 和Majlender P. 提出求解OWA 算子权向量的熵最大化规划模型^[46]和方差最小化规划模型^[47]之后，郭亚军、姚远等以样本的集结过程中权重的熵值为主要考虑因素，给出了非线性规划法来确定时间权向量的一种方法^[48]； 郭亚军、唐海勇等运用最小方差法寻找一组最稳定的时间权重系数来集结样本值，通过求解非线性规划问题来确定时间权向量^[49]。还有一些文献虽然也考虑了时序因素的影响^[50][51][52]，但这些文献在确定时间权向量时，有的是选用上述第一种方法进行的，然而更多的文献是采用主观均分法或AHP 法，或者专家直接赋值法确定的。笔者认为，这些方法主观性太强，并且时间变量的差异性无法客观体现，这显然是不能满足动态决策需要的，也无法客观真实的反映问题。而Fullér 和Majlender、郭亚军等学者提出的最大熵值法和最小方差法这两种方法，为我们科学的确定时间权向量提供了新的思路，但是笔者也认为，郭亚军、唐海勇等（2010） 在求权重系数的方差时，默认每个时间样本点等可能的取得其对应权值，即认为时间权向量的每个分量取对应权值的概率是相等的，都主观赋予了相同的概率1/l，这样处理不具有一般性，在实际应用中具有一定的局限性。鉴于此，本节在现有研究的基础上，引入标准正态分布，利用该分布的良好性质，根据不同时间样本点的权重系数，计算其对应取值的概率，然后在时间度给定的情况下，尽可能地寻找一组时间权系数使其波动最小，提出了一种新的最小方差规划模型来确定动态系统集结的时间权向量。

在确定动态多指标评价系统中的时间权向量时，既要充分考虑决策者的知识和经验等主观因素，又要兼顾时间样本点本身所包含的客观信息，因此我们采用主客观相结合的方法来确定时间权重系数。设动态评价系统的属性集为u = {u1，u2，…，um} ，评价方案集为o = {o1，o2，…，on} ，共有l个时间样本点集t={t1，t2，…，tl} ，并记该时间样本点集t 的权向量为ξ=。在给出确定的数学规划方法之前，在此先引入时间度θ 的定义式^[53]：

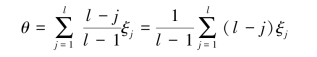
时间度θ 的大小反映了动态评价过程中对时序的重视程度（见表6-5），其取值范围为θ ∈[0，1] 。当θ 越趋近于左端点0 时，表明评价者越重视距评价时刻tl 较近期的数据； 当θ 越趋近于右端点1 时，表明评价者越重视距tl 较远期的数据； 当θ = 0.5 时，表明评价者对各个时间样本点的重视程度相同。^[54]特别地，当ξ=（1，0，…，0）T 时，θ=1； 当ξ=（0，0，…，1）T时，θ = 0； 当ξ = （1/l，1/l，…，1/l）T 时，θ = 0.5。

表6-5　时间度θ 的标度参考表

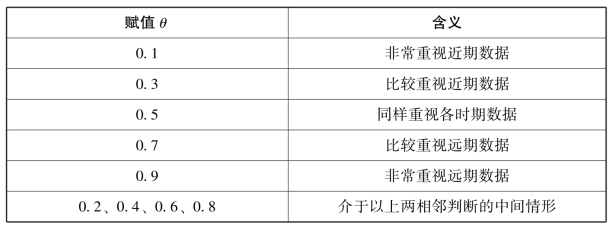
最小方差法确定ξ =（ξ1，ξ2，…，ξl）T 的准则是：在给定时间度θ 的条件下，尽可能地寻找一组最稳定的时间权系数来进行样本值的集结，即寻找一个时间权向量使其波动最小。^[55]而反映权系数波动性特征的指标可用其方差来表示，郭亚军等（2010） 给出的权向量的方差为其中， 表示时间权向量的均值。笔者认为，在此方差的

计算公式中，默认时间权向量的每个分量以等概率1/l 取其对应权值，这样处理只是考虑了一种特殊情况，并不具有一般性，在实际应用中具有一定的局限性，因此得到的结果会有失合理性。为此，下面引入标准正态分布，利用该分布的良好性质，根据不同时间样本点的权重系数计算其对应取值的概率，然后在时间度给定的情况下，尝试将最小方差法进行了改进，通过使时间权向量的方差最小，尽可能地寻找一组最稳定的时间权系数取值，即求解如下的非线性规划问题：

其表示标准正态分布的概率密度函数。此时时间权向量的方差定义为时间权向量的均值为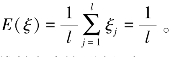将标准正态分布的密度函数带入并化简后，可得该非线性规划问题即为：

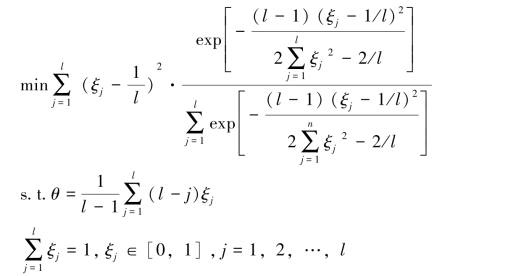
这个非线性规划问题比较复杂，可以借助计算机程序求解，这里我们采用Matlab 中的“内点法（interior-point） ”或者“积极集SQP 滤子方法（active-set） ”来求解，前者对约束条件要求误差较小，但是计算时间较长； 后者对约束条件误差大一些，优点是计算更快。通过对计算结果的比对，我们选用“interior-point”法求解，并且目标函数误差设定为1 × 10-10时所得到的结果。其中，当l=6，取时间度θ=0.1 时，由郭亚军等（2010）给出的最小方差法求得的时间权向量为

ξ′ = (0.0000，0.0000，0.0000，0.0833，0.3333，0.5833)T

对应目标函数的最优值是min′ =0.048611，而由本书给出的改进的最小方差规划模型求得的时间权向量为

ξ = (0.0000，0.0000，0.0439，0.1067，0.1550，0.6944)T

此时对应目标函数的最优值为min = 0.021818。

同时，其他θ 值下的时间权向量分别如表6-6 和表6-7 所示：其中表6-6表示郭亚军等（2010） 给出的最小方差法求得的时间权向量，表6-7 表示本书给出的新的最小方差规划模型求得的时间权向量。

表6-6　不同θ 值下的时间权向量结果（1）

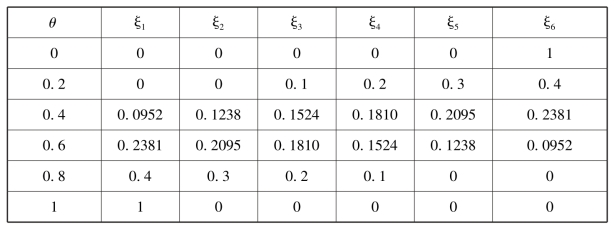
表6-7　不同θ 值下的时间权向量结果（2）

下面不妨以l = 6、时间度θ = 0.1 时的情形为例，将这两种方法所得结果加以比较，可得结论如下：一方面，时间权向量ξ 的取值比ξ′更能体现出时间度θ = 0.1 所表达的意义； 另一方面，对应目标函数的最优值min =0.021818 ＜0.048611 = min′ ，这表明本书提出的方法所确定的时间权向量相比之下更具稳定性。同理，由表6-6 和表6-7 可知，对其他θ 值下的计算结果也有同样的结论。因此可以说，在确定动态评价系统中的时间权向量时，本书提出的新的最小方差规划模型具有较强的合理性和优越性。