指标的规范化,也称为指标数据的无量纲化或标准化,即运用合适的数学函数以消除原始指标量纲对评价结论影响的过程,该过程合理与否直接影响到最终结论的合理性。指标数据的规范化是实现信息综合集成并决策的前提和基础,为此学者们提出了多种行之有效的方法[14][15][16]。但是关于动态综 合评价中的数据规范化处理问题,却基本还在沿用静态的处理方法而忽略了不同时序的差异,以及存在研究缺乏系统性等不足,这样将直接影响决策结论的准确度和可信度。因此,对动态综合评价指标的规范化预处理等问题进行深入研究具有重要的理论价值和现实意义。
6.1.2.1 指标数据规范化预处理的必要性
在多指标评价问题中,往往需要对较复杂的社会经济现象进行统计分析,而对具体问题的统计分析又离不开统计指标体系,因为统计指标体系能从不同侧面对复杂系统的数量特征进行描述与分析。但是在多指标评价的过程中,常会遇到由于不同指标之间量纲和数量级不同而存在着不可公度性的问题,也就是说难以将众多统计指标数据直接加以比较而进行综合评价。多指标评价常常需要借助于各种各样的统计集成方法,如聚类分析法、主成分分析法、神经网络分析法、灰关联度分析法等,此时就需要统计指标之间具有可综合性。然而各统计指标由于表达的意义不同、性质不同、形式不同、计量单位也不同,并且指标的优劣判断标准也可能不同,如有的指标是越大越好型,有的是越小越好型,还有的是达到某个适度值最好等,这样使得评价系统中的指标往往缺乏综合性。此外,如果直接将不同量纲的指标原始值加以评价计算,就会突出取值较大指标的作用,而相对削弱取值较小指标的作用,这样将会使各指标以不等权参与综合评价。[17]因而,为了尽可能客观准确地反映评价对象的真实情况,避免指标系统中统计数据不具备可比性和可综合性等问题,在多指标评价过程中有必要对指标的统计数据做规范化预处理。
而动态多指标评价问题又是传统意义下的静态多指标评价问题的扩展,其中各方案对应的不同指标属性值和权向量均随时间的改变而改变,因此在分析这类问题时不仅要考虑各方案对应的各指标在每个时段的优劣程度,还要考虑各方案对应的各指标在不同时段的增长程度,如果这时还用静态的多指标评价指标预处理方法显然是不甚合理的,所以说,我们对动态多指标评价问题中的指标规范化预处理方法进行研究是十分必要的,也是非常重要的。
6.1.2.2 指标数据规范化预处理的方法
目前已提出的评价指标规范化方法很多,但这些研究基本都只是局限于某一特定时刻的各指标的规范化处理问题,而在带有多个时序的动态多指标评价问题中,如果继续沿用这些静态处理方法,就会忽略掉原始数据间所隐含的增量信息,所得结论就会有失客观性和科学性。这些已有的规范化公式还存在以下不足:有的公式要求指标取正值,这对于有些实际问题并无法满足; 有的公式没有考虑某些指标的特殊取值情况,这样使得研究缺乏全面性和系统性; 公式没有考虑不同时序的差异性等。另外,在实际应用中常会遇到同一被评价对象采用不同规范化方法得出结论不一致的问题,这给具体的评价分析工作也带来了一定的困难。近年来,有学者研究了动态多指标评价中的指标规范化方法:于新锋等(2004) 针对效益型、成本型、固定型、区间型、偏离型和偏离区间型指标分别给出了一类规范化公式[18]; 易平涛等(2009) 针对正向指标,提出了功效系数法的三种动态表示方法[19],这些研究为动态多指标决策理论的探讨提供了新的视角,但是这些方法的适用范围、研究对象同样存在着一定的局限性。因此,针对现有研究的不足和局限性,并借鉴已有研究的成果和思想,笔者尝试性地对四种常用类型的指标,提出了五种拓展的考虑时序的动态多指标评价数据规范化方法,并引入算例对这五种方法的特点和适用范围进行了说明。
设动态多指标评价问题的指标集为u={u1,u2,…,um} ,评价方案集为o = {o1,o2,…,on} ,共有l 个时间样本点集t = {t1,t2,…,tl} ,决策方案ok 对应于时段tj 、指标ui 的原始统计数值序列为{xik(tj)} ,规范化预处理后的指标值序列记为{yik(tj)} ,其中i = 1,2,…,m,k = 1,2,…,n,j = 1,2,…,l。为了以下讨论问题的方便,这里定义符号系统:U ={1,2,…,m} ,O = {1,2,…,n} ,T = {1,2,…,l} 。
根据评价指标自身的内涵,一般可以将其分为以下六类,即效益型属性指标、成本型属性指标、适度型属性指标、区间型属性指标、偏离型属性指标和偏离区间型属性指标等。[20]鉴于在实际问题中常用指标主要是前面四类,本书只讨论前四类指标的规范化预处理方法。其中效益型属性指标也称为正向指标,是指其取值越大越好型的指标,将集合u 中这类指标的下标集记为I1; 成本型属性指标也称为逆向指标,是指其取值越小越好型的指标,将集合u 中这类指标的下标集记为I2; 适度型属性指标也称为固定型指标,是指其取值越趋近于某个最优值xi0 (或者说固定点) 越好型的指标,将集合u 中这类指标的下标集记为I3; 区间型属性指标是指取值越靠近某个最优区间越好,落在最优区间内为最好的指标,记指标ui 的最优区间为D(i) =![]() ( i =1,2,…,m),将集合u 中这类指标的下标集记为I4。显然在同一动态多指标评价问题中,有U = I1 ∪I2 ∪I3 ∪I4。
( i =1,2,…,m),将集合u 中这类指标的下标集记为I4。显然在同一动态多指标评价问题中,有U = I1 ∪I2 ∪I3 ∪I4。
(1) 标准化法:当i ∈I1 ∪I2 时:记动态评价指标的样本均值和样本均方差分别为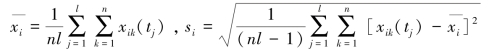
则:

当i ∈I3 时:记动态评价指标与最优值偏差的样本均值和样本均方差分别为:
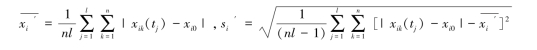

性质分析:对规范化预处理后的指标有E(Yik(tj)) = 0,D(Yik(tj)) = 1(特殊情况除外),且对∀i ∈U,该方法都适用。但yik(tj) ( i = 1,2,…,m,k=1,2,…,n,j=1,2,…,l) 的取值范围不定,即随指标样本值的不同,处理后所得数值的最大值、最小值而不同,当样本观测值离样本均值越近,其处理值离零越近。该方法的优点是考虑了所有指标xik(tj) ,较充分地利用了原始指标数据的所有信息,在多元统计评价方法中应用广泛。但是该方法在消除指标量纲和数量级的同时,也消除了各指标变异程度上的差异。
(2) 极值化法: ![]()

性质分析:规范化预处理后的指标值yik(tj) ∈[0,1] ( i =1,2,…,m,k = 1,2,…,n,j = 1,2,…,l),并且对∀i ∈U,该方法都适用。也就是说,所有类型指标的处理值都满足:最大值为1,最小值为0,便于进行比较和综合。但是该方法只考虑了指标的一些特殊取值,如最大值与最小值、最优值或最优区间的端点,并没有充分利用指标的所有信息。
(3) 归一化法:当i ∈I1 ∪I2 时:
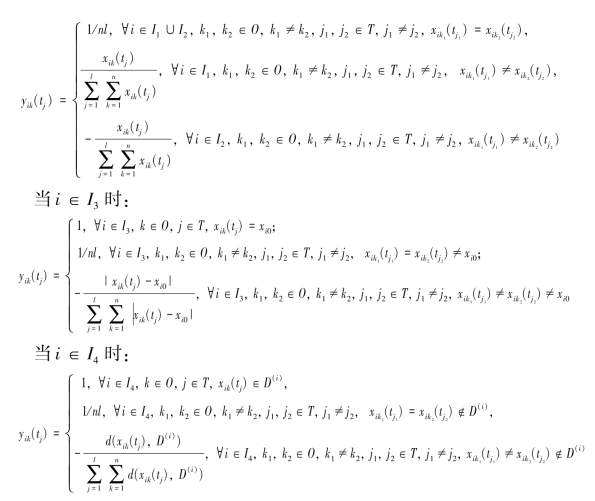


性质分析:对规范化预处理后的指标有E(Yik(tj))= ±1,方差却不为常数,与各指标的变异系数有关(特殊情况除外),且对∀i ∈U,该方法都适用。但yik(tj)∈(-∞,+∞)( i= 1,2,…,m,k= 1,2,…,n,j= 1,2,…,l),即取值范围不定,随指标样本值的不同,处理后所得数值的最大值、最小值而不同。该方法的优点是考虑了所有指标xik(tj) 的原始数据提供的信息,且保留了各指标数据变异程度的信息,满足
(5) 向量规范法: 当i ∈I1 ∪I2 时:
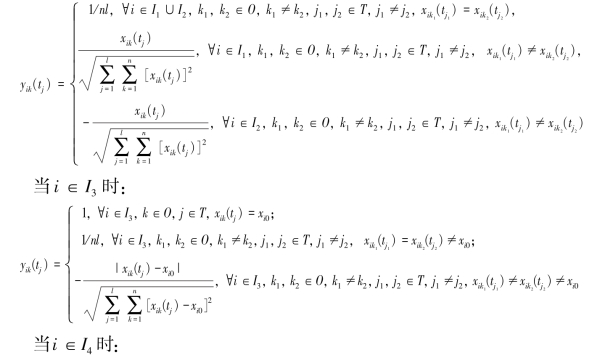
 (https://www.daowen.com)
(https://www.daowen.com)
性质分析:规范化预处理后的指标值满足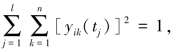 且当
且当![]()
![]() 并且对
并且对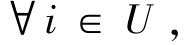 该方法都适用,充分考虑了所有指标的信息。
该方法都适用,充分考虑了所有指标的信息。
在上述五种方法中,特别地,当l=1 时,即为静态规范化方法; 当l ≥2 时,即为动态规范化方法。可见,已有的静态规范化方法是我们所提出的这五种动态规范化方法的一种特例,即上述五种动态规范化方法拓展了静态规范化方法。
当然,以上讨论的只是线性规范化方法,即在规范化预处理前后,指标原始值和处理值之间满足线性关系,亦即指标实际值的变化将导致处理值相应比例的变化。在多指标评价问题中,直线型规范化方法因其简便直观性最为常用,我们提出的这些线性动态规范化方法也可广泛应用于动态多指标评价问题中,而非线性规范化方法处理动态多指标评价问题时亦可按上述思路进行改进。
6.1.2.3 应用数值算例
为了验证上述五种动态规范化方法的合理性,在此笔者选用郭亚军(2002) 给出的算例数据(见表6-1)[21]进行比较分析,即此处的动态多指标评价系统为:u = {u1,u2,u3,u4} ,o = {o1,o2,…,o5} ,t = {t1,t2,t3,t4} ,下面运用本书中提出的五种拓展的动态多指标规范化方法进行处理。
表6-1 时序动态原始数据表
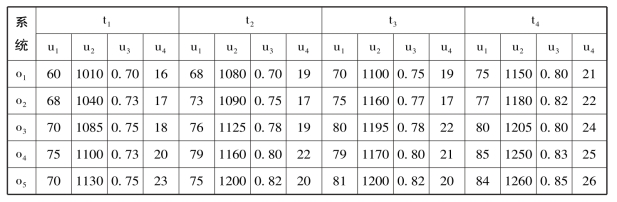
分别运用标准化法、极值化法、归一化法、均值化法和向量规范化法的对应公式,将该决策系统中的数据进行规范化预处理,结果见表6-2、表6-3和表6-4。
表6-2 动态标准化法、极值化法处理结果
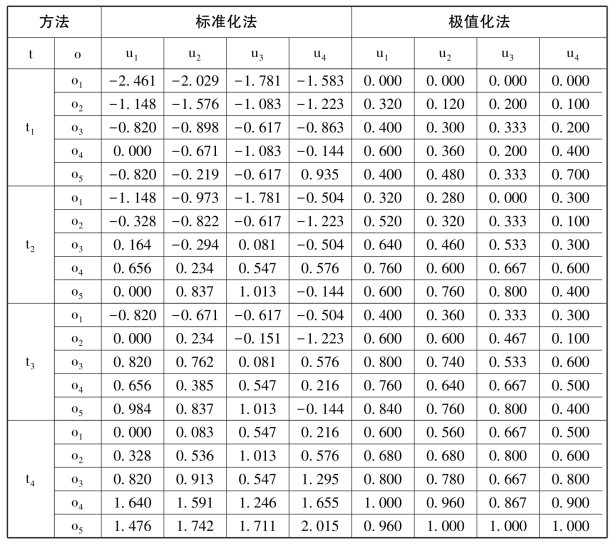
表6-3 动态归一化法、均值化法处理结果
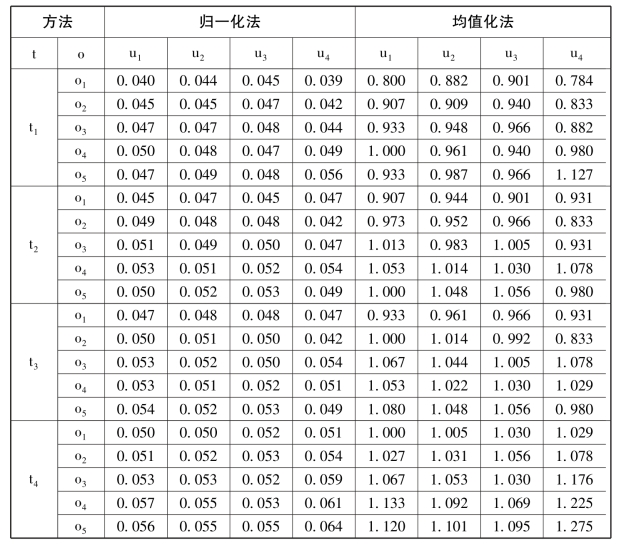
表6-4 动态向量规范化法处理结果
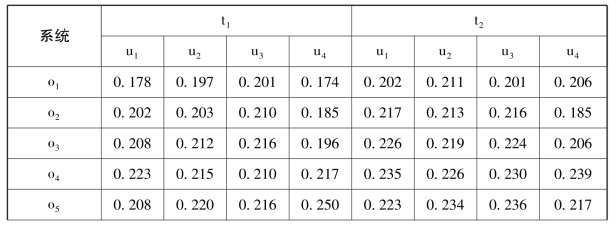
续表

将表6-2、表6-3 和表6-4 中的数据进行仔细分析,我们可以得到如下结论:
(1) 运用上述五种动态多指标规范化方法对原始数据进行预处理,所得结果都在一定程度上保留了原始数据之间的动态增量信息,即处理后的数据能够反映出各方案对应的各指标在不同时段的增减信息。也就是说,这些方法所处理的结果既保留了同一指标在不同时期的变化趋势,也保留了不同评价方案间的差异信息。例如,任意选取两个决策方案o3、o4 的指标u2 在时间点(t1,t3) 的原始取值分别是(1085,1195) 和(1100,1170) ,采用传统的静态标准化方法进行规范化处理,得到的结果是(0.250,0.750) 和(0.564,0.125) ,显然o4 从t1 到t3 的增量信息没有被反映出来。但是采用上述五种动态规范化方法,处理后的结果分别是(- 0.898,0.762) 和(-0.671,0.385) 、(0.300,0.740) 和(0.360,0.640) 、(0.047,0.052) 和(0.048,0.051) 、(0.948,1.044) 和 (0.961,1.022) 以 及 (0.212,0.233) 和(0.215,0.228) ,可见无论是不同时期的变动信息,还是不同方案的差异信息,这些结果都和原始数据保持了同样的增减趋势。这表明文中提出的五种动态多指标规范化方法,对动态多指标评价数据进行预处理是具有有效性和合理性的。
(2) 这五种方法各有特点,规范化处理后得到的数值也存在较大差异。对于归一化法,由表6-3 易见所有的数值比较接近,此处有yik(tj) ∈[0.039,0.064] ( i = 1,2,…,m,k = 1,2,…,n,j = 1,2,…,l),这表明不同处理值之间的差距很小,将这样的数值代入集结模型计算,会忽略各指标差异性的影响; 另一方面,该方法保留了原始数据之间的动态增减信息,但却不能确保不同对象间增量的差异性,例如,指标u2 在t1、t3 下o4相对于o3 的改变量分别为Δx = 15,Δx′ =- 25,但是归一法规范化处理值的改变量却是Δy = 0.001,Δy′ =- 0.001,忽略了增量的差异性。对于极值化法,由表6-2 可知所有的处理值yik(tj) ∈[0,1] ,便于进一步的比较和综合,而且对指标数据的个数和分布状况没什么要求,但由于公式中只考虑了指标值与最大最小值,使得处理值只与每个指标的最值有密切关系,而没有充分考虑每个指标的所有信息。对于标准化法,由表6-2 可知指标处理值的样本均值为0,样本方差为1,利用了每个指标的所有信息,但是不难发现处理值有正有负,偏差较大,使得决策结果可能对指标的依赖性较强。对于向量规范法,由表6-4 可知此处所有的yik(tj) ∈[0.174,0.283] ,即处理值之间的差距较小,使得决策结果可能会忽略各指标的差异性。对于均值化法,由表6-3 可知指标处理值的样本均值为0,样本方差却不一样,考虑了所有指标的信息,且保留了各指标数据变异程度的信息。
综上所述,文中提出的五种动态多指标规范化方法拓展了静态规范化方法,它不仅保留了不同决策方案间的差异信息,而且还体现了同一指标在不同时间样本点的增减趋势。因此,在实际应用中,该方法能更好地反映动态多指标评价问题的现实情况。
6.1.2.4 指标数据规范化预处理方法的选择
目前已提出的数据规范化方法很多,但问题是对同一个评价对象,各种规范化方法得出的结论往往不一致,这就给实际的评价分析工作带来了很大的困难。因此在具体的动态多指标评价问题中,如何选择合适的数据规范化处理方法就显得尤为关键。事实上,正如有的学者所说,理想的规范化方法是不存在的,因此我们在选择时应该注意以下问题,寻求合适的方法,客观科学的反映问题。
(1) 厘清指标原始值与处理值之间的关系,选择合适类型的处理方法。根据指标原始值与处理值之间的函数关系,可将处理方法分为直线型、折线型和曲线型等。[22]其中直线型规范化方法因其简单直观最为常用。在具体的决策分析时,要根据实际问题的需要,以及被研究对象的属性,合理地确定合适类型的规范化处理方法。厘清二者之间是线性关系还是非线性关系:如果是线性的,则选用直线型动态规范化方法加以处理; 如果是非线性的,则可先利用诸如取对数等数学变换将之线性化后再行处理,或直接选用折线型或曲线型规范化方法处理,以求尽可能客观地反映指标实际值与事物发展综合水平间的对应关系。
(2) 熟悉每种方法的特点和适用范围,选择合适的方法和相对应的公式。选用规范化预处理公式时,要注意研究目的和转化方法自身的特点,这样才能达到转化的目的。例如,我们前面提出的五种规范化预处理方法就各有特点,规范化处理结果也有较大差异,因此在实践中要了解指标的属性,分清楚指标所属的类型,结合评价问题自身的要求和每种方法自身的特性,选择相对科学合理的数据预处理方法。
(3) 遵循保序性和简便直观性原则,力求评价分析的客观性和科学性。在决策分析中,并非越复杂的方法越好,关键在于是否切合实际问题的要求,在于是否能够确保每个指标在预处理前后的序关系保持不变,在于是否能够保留原始数据间的动态增量信息。在此前提下,越简明直观越便于应用的方法就是最合适的方法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







