【任务描述】

（1）了解滤波的概念。

（2）认识无源滤波。

（3）掌握用集成运放组成的有源滤波电路。

【知识学习】

一、滤波器

1.作　用

滤波器的作用是允许规定频率范围之内的信号通过，而使规定范围之外的信号不能通过（即受到很大的衰减）。

2.分　类

低通滤波器：允许低频信号通过，将高频信号衰减。

高通滤波器：允许高频信号通过，将低频信号衰减。

带通滤波器：允许某一频率范围的信号通过，将此频带以外的信号衰减。

带阻滤波器：阻止某一频带范围的信号通过，而允许此频带以外的信号通过。

3.无源滤波器

如图4.3.1所示为无源滤波器及幅频特性。

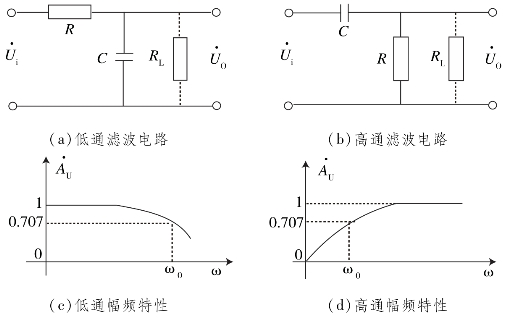
图4.3.1　无源滤波器及幅频特性

（1）无源RC低通滤波器。

如图4.3.1（a）所示，用RC构成最简单的低通滤波器，其电压传输系数为：

式中：ω0=

由上式可知，当信号频率ω由零逐渐增加时，Au将由1逐渐下降，当ω=ω0时，Au=0.707，ω0称为低通滤波器的上限截止频率，其通带为0～ω0，由于只有一个储能元件C，故称为一阶无源低通滤波器。

（2）无源高通滤波器。

如图4.3.1（b）所示，用RC构成最简单的高通滤波器，其电压传输系数为：

式中：ω0=，由上式可知，当信号频率ω由零逐渐增加时，Au将由0逐渐上升，当ω=ω0时，Au=0.707，当ω趋于无穷大时，Au上升为1。ω0称为高通滤波器的下限截止频率，其通带为ω0～∞，由于只有一个储能元件C，故称为一阶无源高通滤波器。

无源滤波电路主要存在如下问题：一是电路增益小，最大仅为1；二是带负载能力差，带上负载会改变截止频率。为了克服上述缺点，可将RC无源网络接至运放的输入端，由于运放需要直流电源才能工作，所以组成的电路称为有源滤波电路。

在有源滤波电路中，集成运放起着放大作用，提高了电路的增益。集成运放的输入电阻很高，故集成运放本身对RC网络的影响小，同时由于集成运放的输出电阻很小，因而大大增强了电路带负载能力。由于在有源滤波电路中，集成运放是作为放大元件，所以集成运放应工作在线性区。

二、有源低通滤波电路

有源低通滤波电路如图4.3.2所示。

下面以图4.3.2（a）为例分析

输出电压为

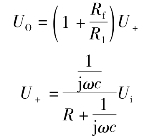
图4.3.2　有源低通滤波器

所以经过推导传递函数为

其中

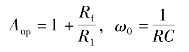
式中：Aup为通带电压放大倍数；ω0为低通最高截止角频率。

低通滤波器的通带电压放大倍数是当工作频率趋于零时，其输出电压Uo与其输入电压Ui的比值。图4.3.3是有源一阶低通滤波器的幅频特性

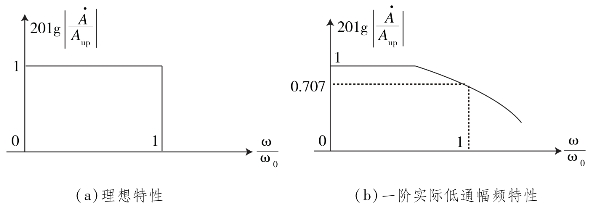
图4.3.3　有源一阶低通滤波器的幅频特性

以同样的方法，可得图4.3.2（b）的特性

式中：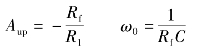

由上述公式可见，我们可以通过改变电阻Rf和R1的值调节通带电压放大倍数，调整RC或Rf C改变截止频率。

一阶滤波电路的缺点是：当ω≥ω0时，频率特性衰减太慢，以-20 dB/10倍程的速度下降，与理想的幅频特性相差甚远。为此可在一阶滤波电路的基础上，再加一级RC，组成二阶（含两个储能元件）滤波电路，它的幅频特性在ω≥ω0时，以-40 dB/10倍程的速度下降，衰减速度快，其幅频特性更接近于理想特性。具体电路如图4.3.4（a）图所示。

图4.3.4　二阶有源低通滤波器

为了进一步改善滤波波型，常将第一级的电容C接到输出端，引入一个反馈，这种电路又叫赛伦—凯电路，实际工作中更为常用。电路如图4.3.4（b）图所示。

三、有源高通滤波电路

有源高通滤波电路如图4.3.5所示。

图4.3.5　有源高通滤波器

下面以图4.3.5（a）图进行分析

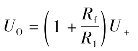
而

所以经过推导传递函数为

其中

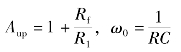
式中：Aup为通带电压放大倍数；ω0为高通下限截止角频率，其幅频特性如图4.3.6所示。

图4.3.6　有源高通滤波器

以同样的方法，可得图4.3.5（b）的特性

式中：(www.daowen.com)

由上述公式可见，我们可以通过改变电阻Rf和R1的值调节通带电压放大倍数，调整RC或R1 C改变截止频率。

与低通滤波电路相似，一阶电路在低频处衰减太慢，为此可再增加一级RC，组成二阶滤波电路，使幅频特性更接近于理想特性。具体电路如图4.3.7所示。

图4.3.7　二阶有源高通滤波器

四、带通滤波电路和带阻滤波电路

将截止频率为ωh的低通滤波电路和截止频率为ωl的高通滤波电路进行不同的组合，就可获得带通滤波电路和带阻滤波电路，如图4.3.8所示。

将一个低通滤波电路和一个高通滤波电路“串接”组成带通滤波电路，如图4.3.9（a）所示，ω＞ωl的信号被低通滤波电路滤掉，ω＜ωl的信号被高通滤波电路滤掉，只有当ωh＞ω＞ωl时信号才能通过，显然，ωh＞ωl才能组成带通电路。

将一个低通滤波电路和一个高通滤波电路“并联”组成的带阻滤波电路，如图4.3.9（b）所示，ω＜ωh信号从低通滤波电路中通过，ω＞ωl的信号从高通滤波电路通过，只有ωh＜ω＜ωl的信号无法通过。

图4.3.8　带通和带阻滤波器原理

图4.3.9　带通和带阻滤波器典型电路

【任务实施】

实训4.3.1　有源滤波电路的研究

一、实训目的

（1）掌握有源低通滤波器和有源高通滤波器的工作原理。

（2）学会对有源滤波电路的调试和频率特性的测试。

二、实训电路和工作原理

（1）图4.3.10（a）所示为有源一阶低通滤波电路图。

图4.3.10　有源一阶低通滤波器电路图及低通滤波幅频特性

图4.3.10中由运放器、反馈电阻Rf与反相输入的电阻R1构成一个正相比例放大器，它的电压放大倍数

在正相输入端，信号源电压Ui经RC网络分压后，在电容C上的电压，即正相输入端a点的电压，由分压公式可得：

由式①和式②，便可得到滤波电路的频率特性

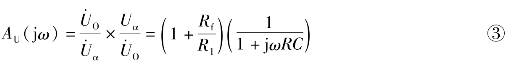
由式③可以看出，是角频率ω的函数。所以可写成AU（jω），AU（jω）即滤波器的频率特性。频率特性AU（jω）可表达为幅频特性A（ω）和相频特性φ（ω）。图4.3.10（b）为理想的低通滤波幅频特性。图中fH为截止频率，它在通频带的高频。图4.3.10（c）为一阶低通滤波电路的幅频特性。

由式③不难看出：当ω（ω=2πf）愈低，则的幅值就愈大；当ω=0时==AUP，AUP为最大值（或峰值）（角标P为峰值peak的第一个字母）。反之，当ω愈高，则愈小。由此可以看出，图4.3.10电路，构成一个低通滤波器。此外，当ω=（即f0=），由式③可得

此时对应的频率称为截止频率，以f0表示，它处在通频带的高端，又以fH表示，此时

图4.3.11（a）为有源一阶高通滤波器电路图。

图4.3.11　有源一阶高通滤波器电路图及高通滤波幅频特性

对照图4.3.10与图4.3.11，不难发现两者的差别：在正相输入端前的RC网络中，R与C做了互换。于是由分压公式可得为：

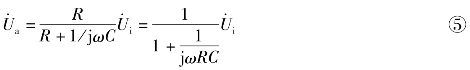
于是有源高通频波电路的频率特性为：

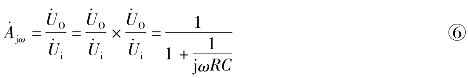
由式⑥可见，ω愈低，则愈小，（ω=0，=0），反之ω愈大，当ω→∞时，图4.3.10（b）为理想高通滤波幅频特性，图中fL为截止频率，它在通频带的低频（the low end）。图4.3.10（c）为一阶高通滤波电路的幅频特性。由以上分析可知，图4.3.11所示电路构成了一个高通滤波器。

同理，在它的截止频率时，称为高通截止频率。以fL表示，它处在通频带的低端。

三、实训设备

（1）装置中的直流±12 V电源（作运放器工作电源），函数信号发生器、双踪示波器、晶体管毫伏表（或数字万用表）。

（2）单元：AX9、R06、R14、C02。

四、实训内容与实训步骤

1.有源低通滤波电路的研究

（1）按图4.3.10（a）所示电路完成接线（包括运放器±12 V工作电源线和地线的接线）。

（2）输入端接函数信号发生器的正弦信号输出。

调节使UiPP（峰-峰值）=4 V，频率f由200 Hz、500 Hz、700 Hz、800 Hz、1.0 kHz、3.0 kHz、5.0 kHz、10 kHz，逐渐加大函数信号发生器输出频率（频率也可用示波器测量），观察输出电压波形。要求在整个频带内不失真。若失真，则调节输入电压UiPP幅值，（一般降低UiPP），使波形不失真。

（3）记录对应上述不同频率下的输出电压峰-峰值UOPP，并计算出滤波电路的电压放大倍数AU=

（4）截止频率f0的测试，在频率f改变时，当UOPP=0.707UOmPP时对应的频率，即为截止频率f0（上式中UOmPP为UOPP的最大值）。

（5）将以上测得的数据填入表4.3.1中。

表4.3.1　有源一阶低通滤波器的幅频特性

2.有源高通滤波器电路的研究

（1）按图4.3.11（a）所示电路完成接线。

（2）与有源低通滤波器实训步骤相同，将所得数据填入表4.3.2中（频率f由高到低进行测试）。

表4.3.2　有源一阶高通滤波器的幅频特性

五、实训注意事项

（1）本实训项目涉及较多电工基础理论，所以要注意复习已学的电工基础知识。

（2）注意输入信号经滤波器后，输出不仅幅值会发生变化，而且相位也会发生变化（与会出现相位差）。

（3）改变信号源Ui的频率时，要注意保持Ui的峰-峰值UiPP不变。

（4）元件、电路和系统的频率特性，在分析它们的性能时很有用，因此对它们要加深理解。

六、实训报告要求

（1）从理论（公式）计算出电路频率特性的截止频率f0。并与测量值进行比较，分析有差别的原因。

（2）由表4.3.1所列数据，画出有源一阶低通滤波器的幅频特性曲线AU（f）（以AU为纵坐标，f为横坐标）。

（3）由表4.3.2所列数据，画出有源一阶高通滤波器的幅频特性曲线AU（f）（以AU为纵坐标，f为横坐标）。