根据《船舶水动力学》《船舶运动及建模》中的知识：螺旋桨进程的相对值称相对进程（也称进速比），船桨的进速比J定义为：螺旋桨回转一周的轴向进程h p（V p=h pn）与桨径D p的比值。

表达式为

式中，V p为螺旋桨的进速；n为螺旋桨转速。

船舶在水中向前航行时，会有三种伴流对螺旋桨产生影响。考虑到在螺旋桨工作时，船对桨及桨对船都会有影响，任何一个因素都会影响到船桨的工作，因此在建立船模型时，引入了两个系数。根据船对桨的影响，引入了伴流系数w；根据桨对船的影响，引入了推力减额系数t。

伴流系数

式中，V s为船舶的速度。

泰勒（Taylor）根据150多艘船舶的实船和船模实验结果获得下列求伴流系数w的经验公式：

式中，Cb是方形系数。推力减额系数为：

式中，ΔP是克服桨的吸水作用产生的阻力而增加的推力；P是螺旋桨提供的总推力。

推力减额系数t可用商赫（Schoenherr）经验公式确定。单桨船基值：(www.daowen.com)

式中C 1的取值根据螺旋桨后装舵类型而定，C 1=0.5～0.7（螺旋桨后装流线型舵）；C 1=0.7～0.9（螺旋桨后装方形尾柱和双板舵）；C 1=0.9～1.05（螺旋桨后装平板舵）。

双桨船值t可用下列经验公式

由螺旋桨的工作机理可知，螺旋桨的推力和扭矩表达式为

式中：P为螺旋桨产生的推力；M为螺旋桨的扭矩；ρ为海水密度；

D P为螺旋桨直径；K P、K M为推力系数及转矩系数。

K P、K M曲线都不是直线，随进速比J增大向下弯曲。一般可认为K P、K M曲线都近似于抛物线，从而可表示为

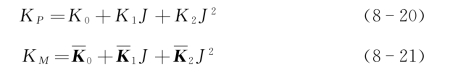
式中系数K 0，K 1，K 2，K 0，K 1，K 2可通过曲线拟合确定。对给定的螺旋桨，它们都是常系数。图8-22为螺旋桨动力特性。

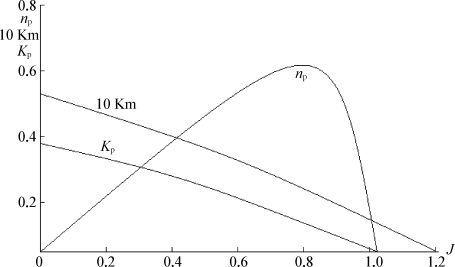
图8-22　螺旋桨动力特性