1.电动机的工作状态

电动机的运行状态根据其电磁转矩与转速方向的关系，分为电动运行和制动运行状态。电动机的电磁转矩方向与转速方向相同时，电磁转矩为克服其轴上的负载转矩而驱动转轴旋转的动力矩，电动机为电动运行状态；而当电动机的电磁转矩方向与转速方向相反时，电磁转矩为阻止其轴上负载运动的阻转矩，电动机处于制动运行状态。

就机械特性曲线而言，当电动机处于电动运行状态时，n与T同为正值或同为负值，曲线位于n-T坐标平面的第1、3象限；而制动运行时，n总与T的方向相反，曲线位于第2与第4象限。

对于由电动机及生产机械构成的电力拖动系统，通常将电动机的机械特性曲线与生产机械的负载特性曲线放在同一n-T坐标平面上。由于生产机械与电动机同轴旋转，当设定电动机的转速和转矩以逆时针转向为正值时，则生产机械的负载转矩为顺时针方向取正值。因此，对于反抗性负载，因负载转矩总与转速的方向相反，故负载特性曲线在坐标的1、3象限；而对于位能性负载，则特性曲线也可能出现在第2或第4象限。

2.电力拖动系统运动方程式

根据刚体运动定律，电力拖动系统运行时的任何瞬间，作用于电动机轴上的转矩必须保持平衡，即

式中，J是拖动系统中折算到电动机轴上的总转动惯量，而 则是系统的转动惯量储存的动能所产生的加速转矩（或称动态转矩）；而则是以飞轮矩GD 2来作为系统转动惯量的量度时的加速转矩的另一种表达式。若以ΔT简单表示加速转矩，则电力拖动系统的运动方程式为

式中T及T L的正负取值由它们与设定转速的正方向关系来决定。即当假定n以逆时针方向为正方向时，则电动机的电磁转矩T逆时针方向时取正，顺时针方向取负；而负载转矩T L逆时针方向取负，顺时针方向取正。加速转矩ΔT的正负则由T和T L的代数和来确定。

当T=T L时，ΔT=0，（d n／d t=0）则n=0或n=定值，拖动系统处于静止状态或恒速运行，为稳定运行状态；

当T＞T L时，ΔT＞0，（d n／d t＞0）拖动系统处于加速的过渡过程中；(www.daowen.com)

当T＜T L时，ΔT＜0，（d n／d t＜0）拖动系统处于减速的过渡过程中。

3.电力拖动系统维持稳定运行的条件

当电力拖动系统由于受到外界干扰（如生产机械负载的变化或电动机外加电压的波动等）时，系统的转速将发生变化而离开原来平衡状态。当干扰消失以后，若系统能自动回复到原来的工作点上，则系统就具备维持稳定运行的条件。

如图1-4（a）所示的是置于同一n-T坐标平面上异步电动机的机械特性曲线和恒转矩负载特性曲线的配合，即电动机带一转矩值为T L的恒转矩负载运行。两条曲线有一交点A，在A点上，T=T L。由电力拖动系统运动方程式可知，动态转矩ΔT=0，所以在A点上该系统能保持一个恒定的转速n 1运行，是系统的一个静态工作点。但系统能否在A点维持稳定运行，则需作进一步的分析。

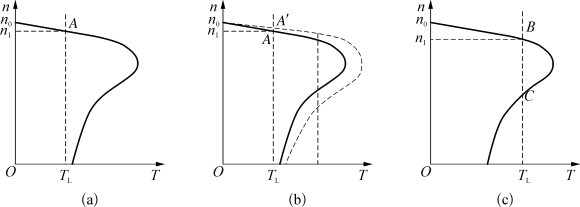
图1-4　电力拖动系统工作点的稳定性判别

如图1-4（b）所示，若拖动系统原来运行在A点上，突然出现瞬时扰动，比如电动机端电压升高，则电动机的电磁转矩T瞬时增大，故T＞T L，ΔT＞0从而使系统加速，在转速上升过程中，电动机转矩随之减小。到达A′点后，电磁转矩和负载转矩又达到新的平衡，系统以新的恒定转速n′1运行。当扰动消除后，T＜T L时，转速下降，系统回复到原来的工作点上。同理，如瞬时扰动引起转速稍有降低，当扰动消失后，则由于T＞T L将使转速回复到原来的数值。因此系统在A点具备维持稳定运行的条件。图1-4（c）所示的是异步电动机带一较重的恒转矩负载，使特性曲线出现两个交点B和C。如果系统运行在B点上，显然它能够维持稳定工作（判别跟前面A点讨论的情况一样）。但如果系统在C点上运行，当突然出现瞬时扰动（如端电压增大）时，电磁转矩T瞬时增大，使电动机加速，n的上升又导致T进一步的增大，使电动机进一步加速，直到B点为止才能进入恒速运行（T=T L）。反之，如果端电压瞬时下降，导致T＜T L时，电动机将从C点减速，转速的降低又使T下降，进一步使电动机减速，直到转速n=0为止。所以在C点上，拖动系统不具备维持稳定运行的条件。

由此可见，电动机机械特性曲线与负载特性曲线的交点是系统的一个平衡点。系统维持稳定运行的条件为：在该交点所对应的转速之上T＜T L，而在交点所对应的转速之下T＞T L。

但是，两条特性曲线的交点并非都是系统的稳定工作点。如图1-4（c）所示为异步电动机驱动较重的恒转矩负载，此时特性曲线出现两个交点B和C。如果系统运行在B点上，显然它能够稳定工作（稳定性判别跟前面A点讨论的情况一样）。如果系统在C点上运行，当突然出现瞬时扰动（如端电压增大）时，电磁转矩T瞬时增大，使电动机加速，n的上升导致T进一步的增大，又使电动机进一步加速，直到B点为止才能进入恒速运行（T=T L）。反之，如果端电压瞬时下降，导致T＜T L时，电动机将从C点减速，转速的降低又使T下降，进一步使电动机减速，直到转速n=0为止。所以选择在C点上工作，拖动系统没有自动回复稳定运行的能力，即C点是系统运行的不稳定工作点。由此可见，对恒转矩负载来说，异步电动机机械特性曲线在临界转差率以下部分为不稳定工作区。

以上的分析可以推广到一般情况下电力拖动系统的稳定性判别：系统在电动机机械特性曲线与负载特性曲线的交点能保持恒速运行；如果在该交点所对应的转速之上T＜T L，而在交点所对应的转速之下T＞T L。那么系统就具有恢复稳定工作的能力，该点即为稳定工作点，反之为不稳定工作点。