普通混凝土是由水泥、砂、石材料用水拌合硬化后形成的人工石材,是多相复合材料。混凝土中的砂、石、水泥胶体组成了弹性骨架,主要承受外力,并使混凝土具有弹性变形的特点。而水泥胶体中的凝胶、孔隙和界面初始微裂缝等,在外力作用下使混凝土产生塑性变形。另一方面,混凝土中的孔隙、界面微裂缝等缺陷又往往是混凝土受力破坏的起源。由于水泥胶体的硬化过程需要多年才能完成,所以混凝土的强度和变形也随时间逐渐增长。
一、混凝土的强度
混凝土的强度是混凝土的重要力学性能指标,是设计混凝土结构的重要依据,它直接影响到结构的安全性和耐久性。在设计施工中常用的混凝土的强度可分为立方体强度、混凝土轴心抗压强度以及混凝土轴心抗拉强度等。
在实际工程中,单向受力构件是极少见的,一般均处于复合应力状态,复合应力作用下混凝土的强度应引起足够的重视。研究复合应力作用下混凝土的强度必须以单向应力作用下的强度为基础,复合应力作用下混凝土的强度实验需要复杂的设备,理论分析也较难,还处以研究之中。因此,单向受力状态下混凝土的强度指标就很重要,它是结构构件分析、建立强度理论公式的重要依据。
1.立方体抗压强度fcu,k
(1)概念 混凝土的强度与水泥强度等级、水灰比有很大关系;骨料的性质、混凝土的级配、混凝土成型方法、硬化时的环境条件及混凝土的龄期等也不同程度地影响混凝土的强度;试件的大小和形状、试验方法和加载速率也影响混凝土强度的试验结果。因此各国对各种单向受力下的混凝土强度都规定了统一的标准试验方法。我国采用边长为150mm的立方体作为混凝土抗压强度的标准尺寸试件,并以立方体抗压强度作为混凝土各种力学指标的代表值。规范规定以边长为150mm的立方体,在20±2℃的温度和相对湿度在95%以上的潮湿空气中养护28天,依照标准试验方法测得的具有95%保证率的抗压强度(以N/mm2计,也就是单位MPa)作为混凝土的强度等级,并用符号fcu,k表示。立方体抗压强度是在实验室条件下取得的抗压强度(标准养护试块)。
(2)强度等级的划分及有关规定 规范规定混凝土强度等级应按立方体抗压强度标准值fcu,k确定。公路桥涵受力构件的混凝土强度等级划分C15、C20、C25、C30、C35、C40、C45、C50、C55、C60、C65、C70、C75和C80,共14个等级。例如,C30表示立方体抗压强度标准值为30N/mm2。其中,C50以下为普通混凝土,C50~C80属高强度混凝土。钢筋混凝土结构的混凝土强度等级不应低于C20;当采用HRB400和KL400级钢筋配筋时,混凝土强度等级不得低于C25。预应力混凝土结构的混凝土强度等级不应低于C40。
(3)试验方法对立方体抗压强度的影响 试件在试验机上受压时,纵向要压缩,横向要膨胀,由于混凝土与压力机垫板弹性模量与横向变形的差异,压力机垫板的横向变形明显小于混凝土的横向变形。①当试件承压接触面上不涂润滑剂时,混凝土的横向变形受到摩擦力的约束,形成“套箍”的作用。在“套箍”的作用下,试件与垫板的接触面局部混凝土处于三向受压应力状态,试件破坏时形成两个对顶的角锥形破坏面,如图2-3a所示,试件是被压坏的。②如果在试件承压面上涂一些润滑剂,这时试件与压力机垫板间的摩擦力大大减小,由于横向变形使混凝土产生横向拉力,试件沿着力的作用方向平行地产生几条裂缝而破坏,所测得的抗压极限强度较低,如图2-3b所示,规范规定的标准试验方法是不加润滑剂。
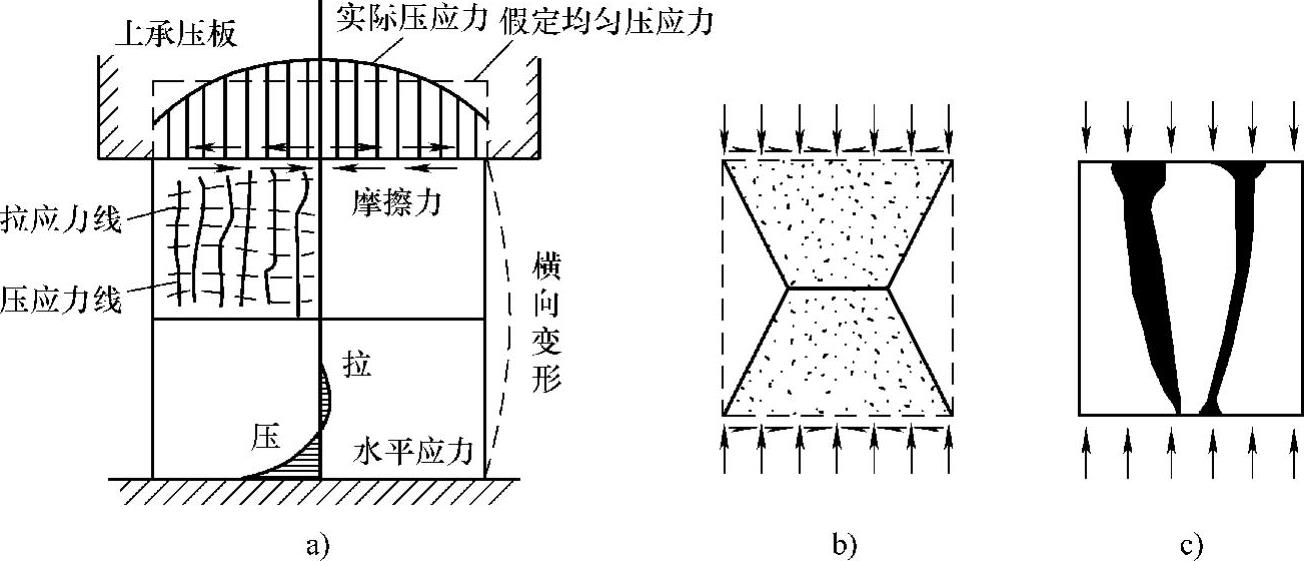
图2-3 混凝土立方体的破坏情况
a)立方体试件的受力 b)承压板与表面之间不涂润滑剂 c)承压板与表面之间涂润滑剂
(4)加载速度对立方体强度的影响 加载速度越快,测得的强度越高。通常规定加载速度为:混凝土强度等级低于C30时,取每秒钟0.3~0.5N/mm2;混凝土强度等级高于或等于C30低于C60时,取每秒钟0.5~0.8N/mm2。混凝土强度等级高于C60时,取每秒钟0.8N/mm2。
(5)龄期对立方体强度的影响 混凝土的立方体抗压强度随着成型后混凝土的龄期逐渐增长,增长速度开始较快,后来逐渐缓慢,强度增长过程往往要延续几年,在潮湿环境中延续时间更长。
(6)尺寸效应 立方体尺寸愈小则试验测出的抗压强度愈高,对此现象有多种不同的原因分析和理论解释,但还没有得出一致的结论。一种观点认为是材料自身的原因,认为试件内部缺陷(裂纹)的分布,粗、细粒径的大小和分布,材料内摩擦角的不同和分布,试件表面与内部硬化程度有差异等因素有关。另一种观点认为是试验方法的原因,认为试块受压面与试验机之间摩擦力分布(四周较大,中央较小)、试验机垫板刚度有关。过去我国曾长期采用以200mm边长的立方体作为标准试件。在试验研究也采用100mm的立方体试件。用这两种尺寸试件测得的强度,与用150mm立方体标准试件测得的强度有一定差距,这归结于尺寸效应的影响。所以非标准试件强度应乘以一个换算系数,换算成标准试件强度。根据大量实测数据,规范规定,现测定立方体强度是采用150mm×150mm×150mm的立方体试件得出的,如采用200mm或100mm的立方体试块时,其换算系数分别取1.05和0.95。
2.混凝土轴心抗压强度fck
由于实际结构和构件往往不是立方体,而是棱柱体,所以用棱柱体试件比立方体试件能更好地反映混凝土的实际抗压能力。试验证实,轴心抗压钢筋混凝土短柱中的混凝土强度基本上和棱柱体抗压强度相同,可以用棱柱体测得的抗压强度作为轴心抗压强度,又称为棱柱体抗压强度。规范规定以150mm×150mm×300mm的棱柱体试件试验测得的具有95%保证率的抗压强度为混凝土轴心抗压强度标准值,用符号fck表示。棱柱体试件与立方体试件的制作条件相同,试件上下表面不涂润滑剂。实测的棱柱体试件的抗压强度都比立方体的强度值低,并且棱柱体试件高宽比越大,强度越小。混凝土轴心抗压强度随着混凝土强度等级提高而增加,总趋势是混凝土轴心抗压强度与混凝土强度成正比。
3.混凝土的轴心抗拉强度ft
混凝土的轴心抗拉强度是混凝土的基本力学指标之一,也可用它间接地衡量混凝土的冲切强度等其他力学性能。轴心抗拉强度只有立方抗压强度的1/18~1/8,混凝土强度等级愈高,这个比值愈小。混凝土的轴心抗拉强度取决于水泥石的强度和水泥石与骨料的粘接强度。采用表面粗糙的骨料及较好的养护条件可提高混凝土的轴心抗拉强度。
但在进行钢筋混凝土结构强度计算时,认为受拉区混凝土开裂后退出工作,拉力全部由钢筋来承受,此时研究混凝土的抗拉强度没有实际意义。但是对于不允许出现裂缝的结构,就应该考虑混凝土的抗拉能力,并以混凝土的轴心抗拉极限强度作为混凝土抗裂强度的重要指标。
轴心抗拉强度可采用如图2-4的试验方法,试件尺寸为100mm×100mm×500mm的柱体,两端埋有伸出长度为150mm的变形钢筋(d=16mm),钢筋位于试件轴线上。试验机夹紧两端伸出的钢筋,对试件施加拉力,破坏时裂缝产生在试件的中部,单位时间的平均破坏应力为轴心抗拉强度。由于混凝土内部的不均匀性,加之安装试件的偏差等原因,这种方法准确测定抗拉强度是很困难的。所以也常用如图2-5所示的圆柱体或立方体的劈裂试验来间接测试混凝土的轴心抗拉强度。
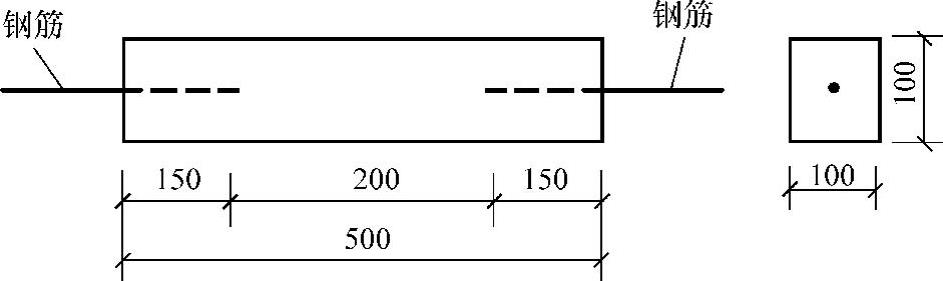
图2-4 混凝土直接受拉实验(尺寸单位:mm)

图2-5 混凝土劈裂实验及其应力分布
a)圆柱体劈裂试验 b)立方体劈裂试验 c)劈裂面上水平应力分布
在立方体或圆柱体上加垫条,在垫条上施加一条压力线荷载,这样试件中间垂直截面除加力点附近很小的范围外,均有均匀分布的水平拉应力。当拉应力达到混凝土的抗拉强度时,试件被劈成两半。根据弹性理论,劈裂抗拉强度可按下式计算:

式中 P——破坏荷载;
d——圆柱直径或立方体边长;
l——试件的长度。
试验结果表明,混凝土的劈裂强度除与试件尺寸等因素有关外,还与垫条的宽度和材料特性有关。加大垫条宽度可使实测劈裂强度提高,一般认为,垫条宽度应不小于立方体试件边长或圆柱体试件直径的1/10。国内外的大多数试验资料表明,混凝土的劈裂强度略高于轴心抗拉强度,考虑到国内外对比资料的具体条件不完全相同,且目前我国尚未建立混凝土劈裂试验的统一标准,通常认为混凝土的轴心抗拉强度与劈裂强度基本相同。
4.混凝土的强度标准值与设计值
经统计分析,并考虑结构混凝土强度与试件混凝土强度之间的差异,选取具有95%保证率的强度值作为强度标准值。混凝土强度设计值为混凝土强度标准值除以混凝土的材料分项系数γc,《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《桥规》)规定γc=1.4,见表2-1。
表2-1 混凝土强度标准值 (单位:N/mm2)
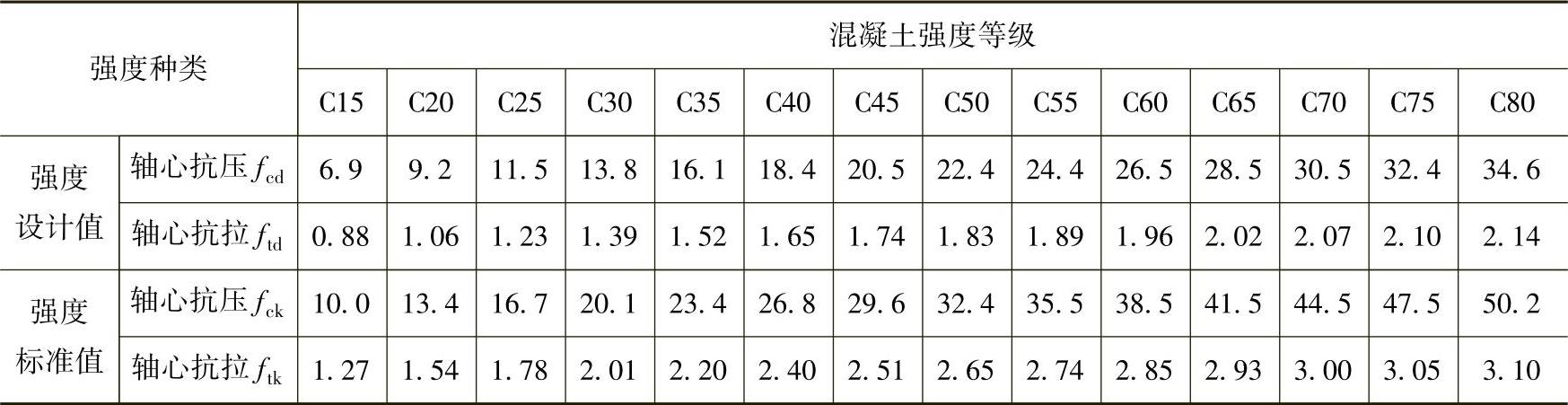
注:计算现浇钢筋混凝土轴心受压及偏心受压构件时,如截面的长边或直径小于300mm,则表中混凝土的强度设计值应乘以系数0.8;当构件质量(如:混凝土成型、截面和轴线尺寸等)确定保证时,可不受此限制。
5.混凝土在复合应力作用下的强度
混凝土结构和构件通常受到轴力、弯矩、剪力和扭矩的不同组合作用,很少处于理想的单向受力状态,实际混凝土结构构件大多处于复合应力状态,例如框架梁、柱既受到柱轴向力作用,又受到弯矩和剪力的作用。节点区混凝土受力状态更为复杂,所以分析混凝土在复合应力作用下的强度就很有必要,对于认识混凝土的强度理论也有重要意义。
(1)双向应力状态下混凝土的强度 如图2-6所示,在两个相互垂直平面,作用着法向应力σ1和σ2(第三个平面上应力为零)的双向应力状态下,其强度变化特点如下:
①双向受拉。图中第一象限为双向受拉区,σ1和σ2相互影响不大,即不同应力比值σ1/σ2下的双向受拉强度均接近于单向受拉强度。
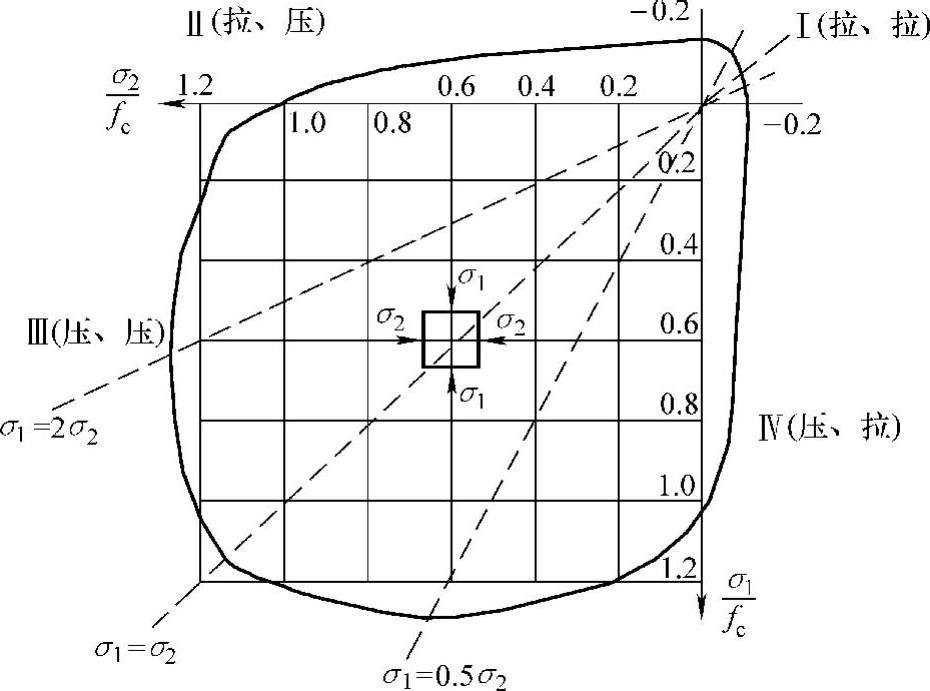
图2-6 双向应力状态下混凝土强度变化曲线
②双向受压。第三象限为双向受压区,大体上是一向的强度随另一向压力的增加而增加。这是由于一个方向的压应力对另一个方向压应力引起的横向变形起到了一定的约束作用,限制了试件的内部混凝土微裂缝的扩展,所以提高了混凝土的抗压强度。当σ1/σ2约等于2或0.5时,混凝土双向受压强度比单向受压强度提高25%左右。当σ1/σ2=1时,仅提高16%左右。
③拉—压状态。第二、四象限为拉—压应力状态,此时混凝土的强度均低于单向拉伸或压缩时的强度。这是由于两个方向同时受拉、受压时,相互助长了试件在另一个方向上的受拉变形,加速了混凝土内部微裂缝的发展,使混凝土的强度降低。
(2)三向受压状态下混凝土的强度 混凝土在三向受压的情况下,由于受到侧向压力的约束作用,最大主压应力轴的抗压强度fcc(σ1)有较大程度的增长,其变化规律随两侧向压应力(σ2,σ3)的比值和大小的不同而不同。混凝土在三向受压时,其最大主压应力方向的抗压强度,取决于侧向压应力的约束程度,随侧向压应力的增加,微裂缝的发展受到了极大的限制,大大地提高了混凝土纵向抗压强度,并使混凝土的变形性能接近理想的弹塑性体。如采用钢管混凝土柱、螺旋箍筋柱等,能有效约束混凝土的侧向变形,使混凝土的抗压强度、延性(耐受变形的能力)有相应的提高。常规的三轴受压是在圆柱体周围加液压,在两侧向等压的情况下进行的。由试验得到的经验公式为:
fcc=fc+Kσr (2-2)
式中 fcc——三向受压时的混凝土轴心抗压强度;
fc——无侧向压力约束试件的轴心抗压强度;
σr——侧向约束压应力;
K——侧向压应力系数,侧向压应力较低时,其值较大,试验资料得出K=4.5~7.0。
二、混凝土的变形
混凝土变形有两类:一类是荷载作用下的受力变形,包括一次短期加载时的变形、多次重复加载时的变形和长期荷载作用下的变形;另一类是体积变形,包括收缩、膨胀和温度变形。
1.一次短期加载下混凝土的变形性能
对混凝土进行短期单向施加压力所获得的应力—应变关系曲线即为单轴受压应力—应变曲线,如图2-7所示,它能反映混凝土受力全过程的重要力学特征和基本力学性能,是研究混凝土结构强度理论的必要依据,也是对混凝土进行非线性分析的重要基础。一般用棱柱体试件来测试,得出混凝土的应力—应变曲线。
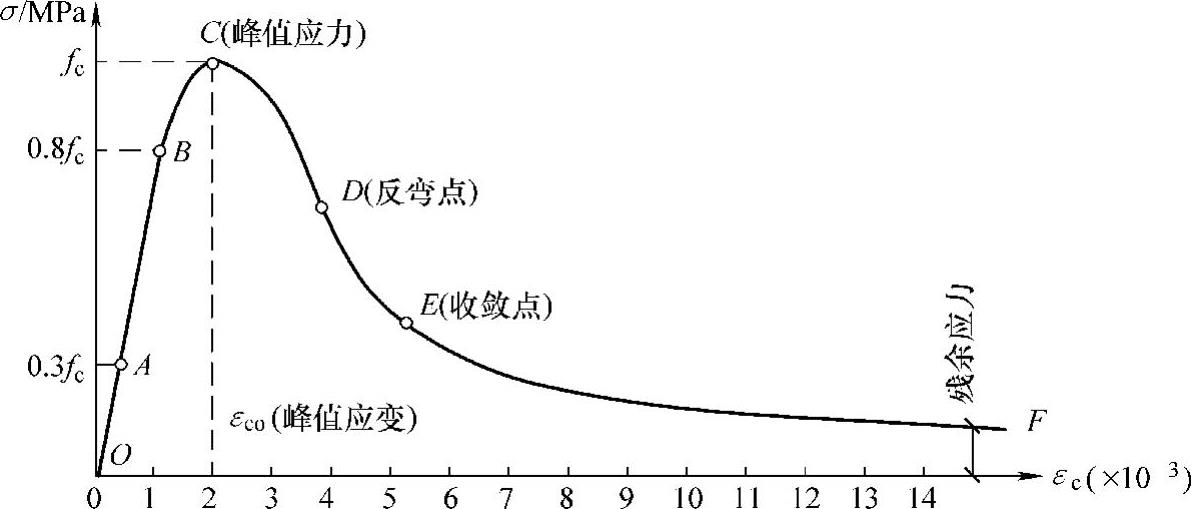
图2-7 混凝土单轴受压应力—应变关系曲线
一次短期加载是指荷载从零开始单调增加至试件破坏,也称单调加载。从图中可看出:全曲线包括上升段和下降段两部分,以C点为分界点,每部分由三小段组成。
图中各关键点分别表示为:A―比例极限点,B―临界点,C―峰值点,D―拐点,E―收敛点,F―曲线末梢。
各小段的含义为:OA段(σ≤0.3fc)接近直线,应力较小,应变不大,混凝土的变形为弹性变形,原始裂缝影响很小,应力—应变关系接近直线;AB段(σ=0.3fc~0.8fc)为微曲线段,应变的增长稍比应力快,混凝土处于裂缝稳定扩展阶段,其中B点的应力是确定混凝土长期荷载作用下抗压强度的依据;BC段(σ=0.8fc~1.0fc)应变增长明显比应力增长快,混凝土处于裂缝快速不稳定发展阶段,其中C点的应力最大,即为混凝土极限抗压强度,与之对应的应变ε0≈0.002为峰值应变;CD段应力快速下降,应变仍在增长,混凝土中裂缝迅速发展且贯通,出现了主裂缝,内部结构破坏严重;DE段,应力下降变慢,应变较快增长,混凝土内部结构处于磨合和调整阶段,主裂缝宽度进一步增大,最后只依赖骨料间的咬合力和摩擦力来承受荷载;EF段为收敛段,此时试件中的主裂缝宽度快速增大而完全破坏了混凝土内部结构,这时贯通的主裂缝已很宽,对无侧向约束的混凝土,收敛段EF已失去结构意义。
由不同强度的混凝土的σ-ε关系曲线(图2-8)比较可知:
①混凝土强度等级高,其峰值应变ε0增加不多。
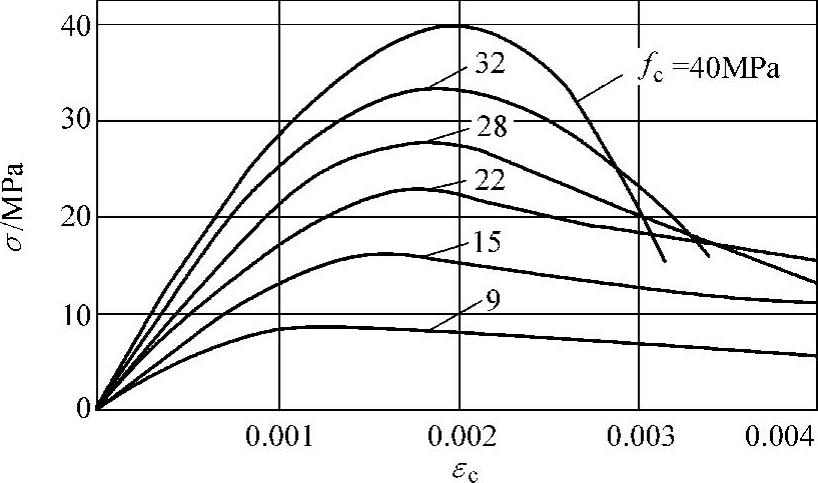
图2-8 强度等级不同的混凝土的应力—应变曲线
②上升段曲线相似。(www.daowen.com)
③下降段区别较大:强度等级低,下降段平缓,应力下降慢;强度等级高,下降段较陡,应力下降很快。
④等级高的混凝土,受压时的延性不如等级低的混凝土。
2.荷载长期作用下混凝土的变形性能(徐变)
混凝土构件或材料在不变荷载或应力的长期作用下,其变形或应变随时间而不断增长,这种现象称为混凝土的徐变。徐变主要由两种原因引起,其一是混凝土具有粘性流动性质的水泥凝胶体,在荷载长期作用下产生粘性流动;其二是混凝土中微裂缝在荷载长期作用下不断发展。当作用的应力较小时主要由凝胶体引起,当作用的应力较大时,则主要由微裂缝引起。
如图2-9所示为100mm×100mm×400mm的棱柱体试件在相对湿度为65%、温度为20℃,承受σ=0.5fc压应力并保持不变的情况下,变形与时间的关系曲线。
由图2-9可知:24个月的徐变变形εcc约为加荷时立即产生的瞬时弹性变形εci的2~4倍,前期徐变变形增长很快,六个月可达到最终徐变变形的70%~80%,以后徐变变形增长逐渐缓慢。徐变的特性主要与时间有关,通常表现为前期增长快,以后逐渐减慢,经过2~3年后趋于稳定。由B点卸载后,应变会恢复一部分,其中立即恢复的一部分被称为混凝土瞬时恢复弹性应变εcir;再经过一段时间,约为20天后才恢复的那部分叫弹性后效εchr,其值约为徐变变形的1/12,最后剩下的不可恢复的应变称为残余应变εcp。
徐变具有两面性,一则引起混凝土结构变形增大,导致预应力混凝土发生预应力损失,严重时还会引起结构破坏;二则徐变的发生对结构内力重分布有利,可以减小各种外界因素对超静定结构的不利影响,降低附加应力。
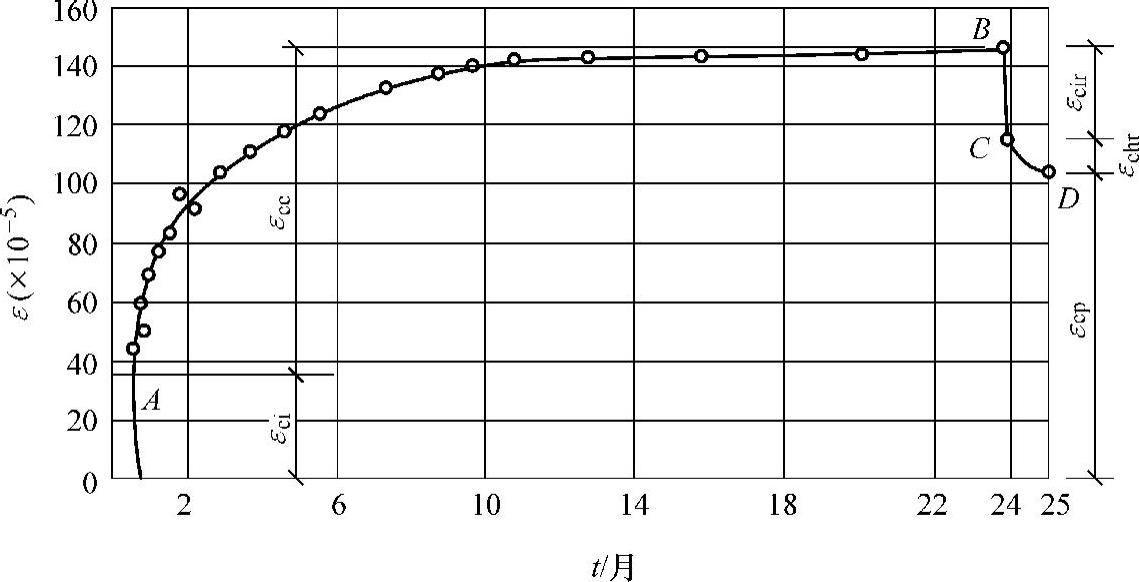
图2-9 混凝土徐变(加荷卸荷应变与时间关系曲线)
影响混凝土徐变的因素是多方面的,概括起来可归纳为三个方面因素,即:内在因素、环境因素和应力因素。
1)就内在因素而言,水泥含量少、水灰比小、骨料弹性模量大、骨料含量多,那么徐变小。
2)对于环境因素而言,养护及使用条件下的温湿度是影响徐变的环境因素。养护时温度高、湿度大、水泥水化作用充分,徐变就小,采用蒸汽养护可使徐变减小约20%~35%。受荷后构件所处环境的温度越高、湿度越低,则徐变越大。如环境温度为70℃的试件受荷一年后的徐变,要比温度为20℃的试件大一倍以上。因此,高温干燥环境将使徐变显著增大,并且构件的体表比越大,徐变越小。
3)应力因素主要反映在加荷时的应力水平,当混凝土应力σc≤0.5fc时,徐变与应力成正比,这种情况称为线性徐变;当混凝土应力σ=(0.5~0.8)fc时,徐变变形与应力不成正比,徐变变形比应力增长要快,称为非线性徐变。在非线性徐变范围内,当加载应力过高时徐变变形急剧增加不再收敛,呈非稳定徐变的现象,可能造成混凝土的破坏。当应力σc>0.8fc时,徐变的发展是非收敛的,最终将导致混凝土破坏。所以混凝土构件在使用期间,应当避免经常处于不变的高应力状态。显然应力水平越高,徐变越大;持荷时间越长,徐变也越大。一般来讲,在同等应力水平下高强度混凝土的徐变量要比普通混凝土的小很多,而如果使高强混凝土承受较高的应力,那么高强度混凝土与普通混凝土最终的总变形量将较为接近。
3.混凝土在荷载重复作用下的变形(疲劳变形)
混凝土在荷载重复作用下引起的破坏称为疲劳破坏。疲劳现象大量存在于工程结构中,钢筋混凝土吊车梁受到重复荷载的作用,钢筋混凝土桥梁受到车辆振动的影响,港口海岸的混凝土结构受到波浪冲击而损伤等都属于疲劳破坏现象。疲劳破坏的特征是裂缝小而变形大。
(1)混凝土在荷载重复作用下的应力—应变曲线(图2-10)
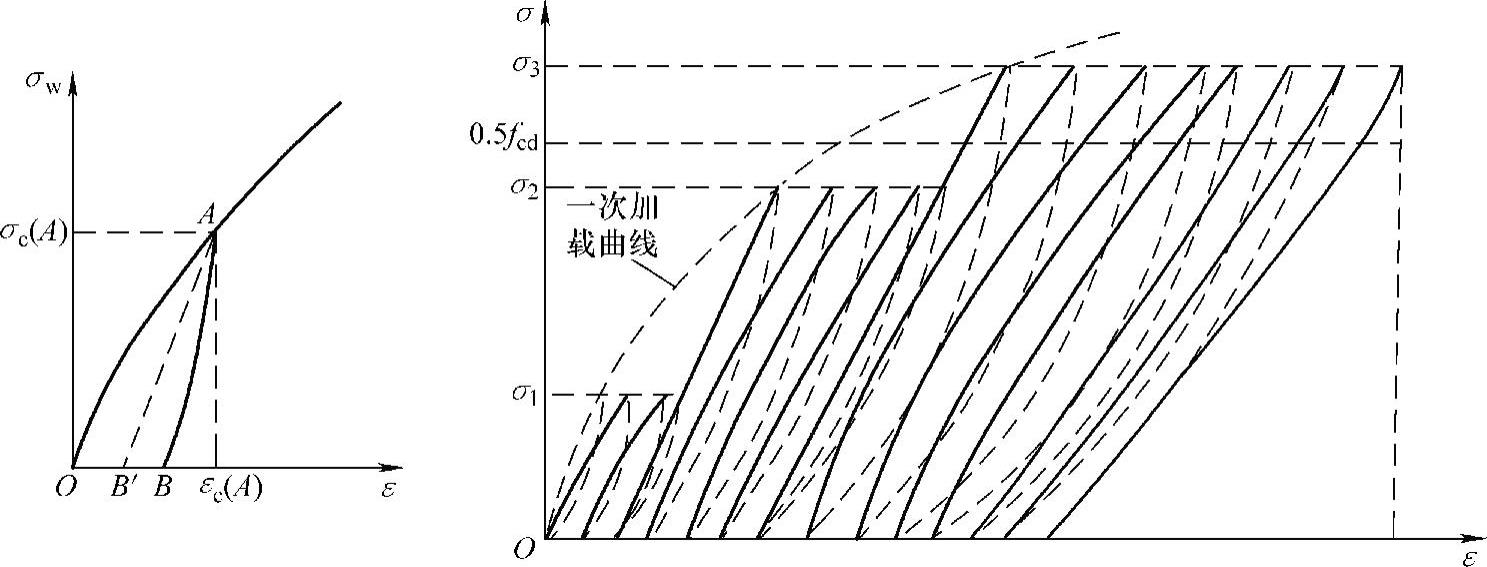
图2-10 混凝土在重复荷载作用下的应力—应变曲线
①σ1或σ2<0.5fc时:对混凝土棱柱体试件,一次加载应力σ1或σ2小于混凝土疲劳强度fcf时,其加载、卸载应力—应变曲线OAB形成了一个环状。而在多次加载、卸载作用下,应力—应变环会越来越密合,经过多次重复,这个曲线就密合成一条直线。
②σ3>0.5fc时:开始时混凝土应力—应变曲线凸向应力轴,在重复荷载过程中逐渐变成直线,再经过多次重复加卸载后,其应力—应变曲线由凸向应力轴而逐渐凸向应变轴,以致加卸载不能形成封闭环,这标志着混凝土内部微裂缝的发展加剧趋近破坏。随着重复荷载次数的增加,应力—应变曲线倾角不断减小,至荷载重复到某一定次数时,混凝土试件会因严重开裂或变形过大而导致破坏。
(2)混凝土的疲劳强度fcf 混凝土的疲劳强度用疲劳试验测定。把能使棱柱体试件承受200万次反复荷载而发生破坏的应力值,称为混凝土的疲劳强度fcf,一般取fcf≈0.5fc。
4.混凝土的变形模量
混凝土的变形模量广泛地用在计算混凝土结构的内力、构件截面的应力和变形以及预应力混凝土构件截面应力分析之中,是不可缺少的基础资料之一。但与弹性材料相比,混凝土的应力应变关系呈现非线性性质,即在不同应力状态下,应力与应变的比值是一个变数。混凝土的变形模量有三种表示方法。
(1)原点模量Ec 原点模量也称弹性模量,在混凝土轴心受压的应力—应变曲线上,过原点做该曲线的切线,如图2-11所示,其斜率即为混凝土原点切线模量,通常称为混凝土的弹性模量Ec,即:
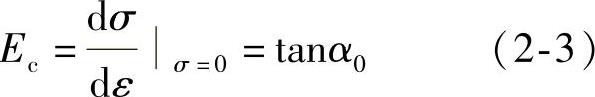
式中 α0——过原点所做应力应变曲线的切线与应变轴间的夹角。
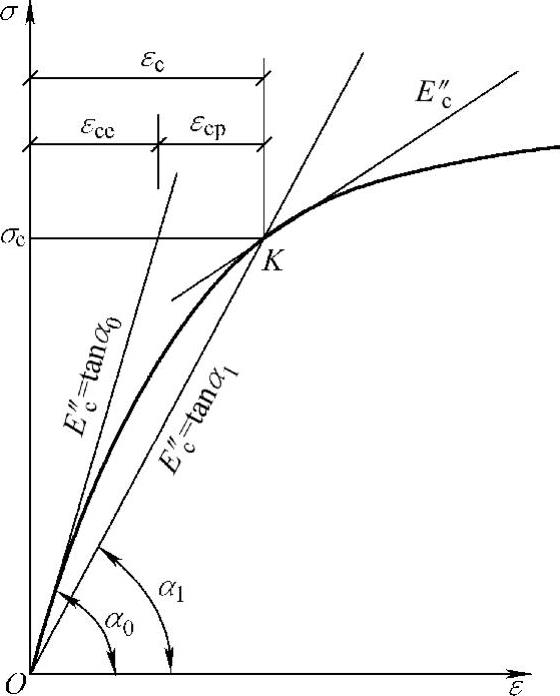
图2-11 混凝土变形模量的表示方法
在实际工作中应用最多的还是原点弹性模量,即弹性模量。按照原点弹性模量的定义,直接在应力—应变曲线的原点做切线,找出α0角是很不精确的,目前各国对弹性模量的实验方法尚没有统一的标准。我国的通常做法是对棱柱体试件先加载至σ=0.5fc,然后卸载至零,再重复加载卸载5~10次,应力应变逐渐趋于稳定,并基本上接近于直线,该直线斜率即为混凝土弹性模量的取值,混凝土强度越高,弹性模量越大,取值见表2-2。
表2-2 混凝土弹性模量(×104) (单位:N/mm2)

按照上述做法,对不同等级的混凝土测得的弹性模量,经统计分析得下列经验公式:

实验表明,混凝土的受拉弹性模量与受压弹性模量大体相等,其比值为0.82~0.995。计算中受拉和受压弹性模量可取同一值。
(2)割线模量Ec′
在混凝土的应力—应变曲线上任一点与原点连线,如图2-11所示,其割线斜率,即为混凝土的割线模量:

由上可知,混凝土的割线模量是一个随应力不同而异的变数。在同样应变条件下,混凝土强度越高,割线模量越大。
(3)切线模量Ec″
在混凝土的应力—应变曲线上任取一点,并做该点的切线,如图2-11所示,则其斜率为混凝土的切线模量,即:

式中 α——应力应变曲线上某点的切线与应变轴间的夹角。
混凝土的切线模量也是一个变数,并随应力的增大而减小。对不同强度等级的混凝土,在应变相同的条件下,强度越高,切线模量越大。
(4)剪切模量
混凝土的剪变模量可根据虎克定律确定,即:

式中 τ——混凝土的剪应力;
γ——混凝土的剪应变。
由于现在尚未有合适的混凝土抗剪试验方法,所以要直接通过试验来测定混凝土的剪切模量是十分困难的。一般根据混凝土抗压试验中测得的弹性模量Ec来确定,即

式中 Ec——混凝土的弹性模量(N/mm2);
νc——混凝土的泊松比。一般结构的混凝土泊松比变化不大,且与混凝土的强度等级无明显关系,取νc=0.2,Gc=0.4Eo。
5.体积变形
混凝土凝结硬化时,在空气中体积收缩,在水中体积膨胀。通常,收缩值比膨胀值大很多。且膨胀常起到有利作用,因此在计算中不予考虑。混凝土的收缩值随着时间而增长,蒸汽养护混凝土的收缩值要小于常温养护下的收缩值。
收缩是混凝土在不受外力情况下体积变化产生的变形,是由混凝土在凝结硬化过程中的化学反应产生的“凝缩”,和混凝土水分的蒸发所产生的“干缩”两部分所引起的。结硬初期收缩变形发展很快,两周可完成全部收缩的25%,一个月完成50%,三个月后增长缓慢,两年后趋于稳定。最终收缩值约为(2~6)×10-4。
当混凝土收缩受到外部(支座)或内部(钢筋)的约束时,将使混凝土内部产生拉应力,甚至引起混凝土的开裂。混凝土收缩会使预应力混凝土构件产生预应力损失。某些对跨度比较敏感的超静定结构(如拱结构等),收缩也会产生不利的内力。
影响混凝土收缩的主要因素有:
1)水泥的用量:水泥越多,收缩越大;水灰比越大,收缩也越大。
2)骨料的性质:骨料的弹性模量大,收缩小。
3)养护条件:在结硬过程中,周围温、湿度越大,收缩越小。
4)混凝土制作方法:混凝土越密实,收缩越小。
5)使用环境:使用环境温度、湿度大时,收缩小。
6)构件的体积与表面积比值:比值大时,收缩小。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






