1.矢量控制基本原理

为了改善电动汽车异步电机的动态特性，应优先选择矢量控制（FOC）而不是VVVF控制。FOC的基本思路是：模拟直流电机的控制方法进行控制，根据线性变换以及变换前后磁势和功率不变的原则，通过正交变换将a-b-c三相坐标下的数学模型变成α-β两相静止坐标系（Clarke）的模型，然后通过旋转变换将两相静止坐标系的模型变成两相旋转坐标系（Park）的模型（d-q）。在α-β/d-q变换下将定子电流矢量分解成按转子磁场定向的两个直流分量i_d、i_q（其中i_d为励磁电流分量，i_q为转矩电流分量），并对其分别加以控制，控制i_d相当于控制磁通，控制i_q相当于控制转矩。

在异步电机磁场定向的矢量控制算法中，将旋转坐标系中d轴放在转子磁场上为转子磁场定向控制，将旋转坐标系中d轴放在定子磁场上称为定子磁场定向控制，将旋转坐标系中d轴放在气隙磁场上称为气隙磁场定向控制，由于后两种控制较难实现，并且电机的电磁转矩表达式是非线性的，因此通常采用转子磁场定向（RFOC）感应电机模型进行分析和控制。

由三相静止坐标系abc变换为两相同步旋转坐标系变换矩阵为

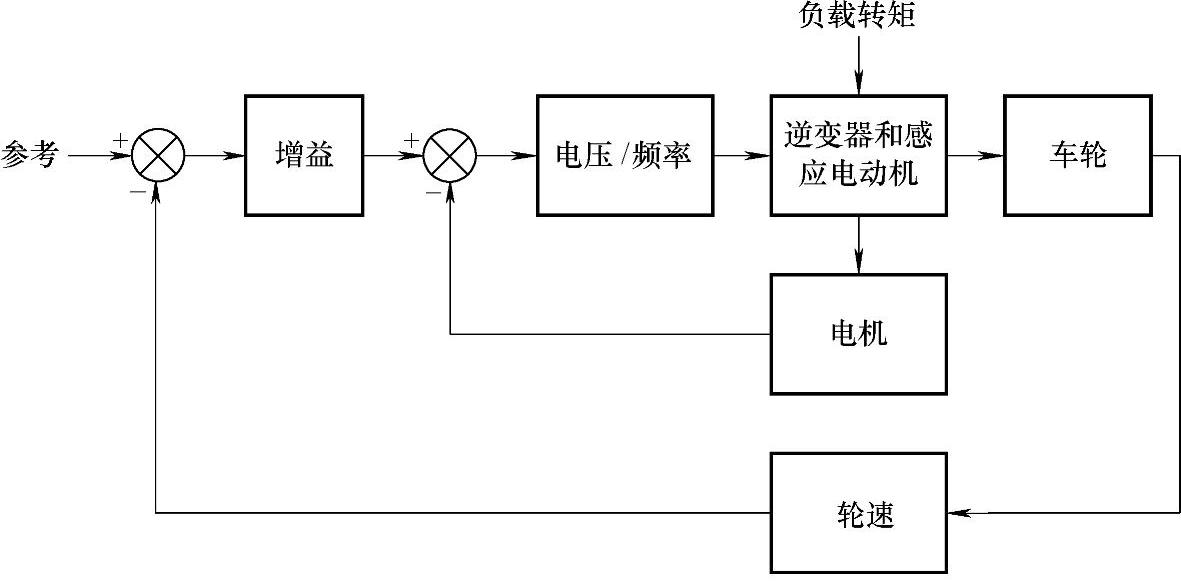
图6-11 异步电机驱动系统VVVF控制功能的框图

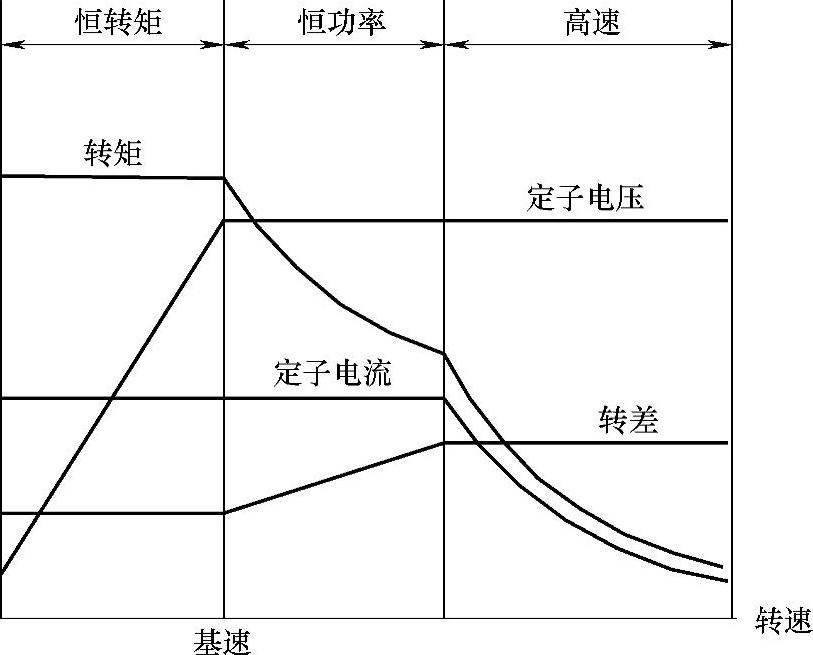
图6-12 异步电机的驱动特性

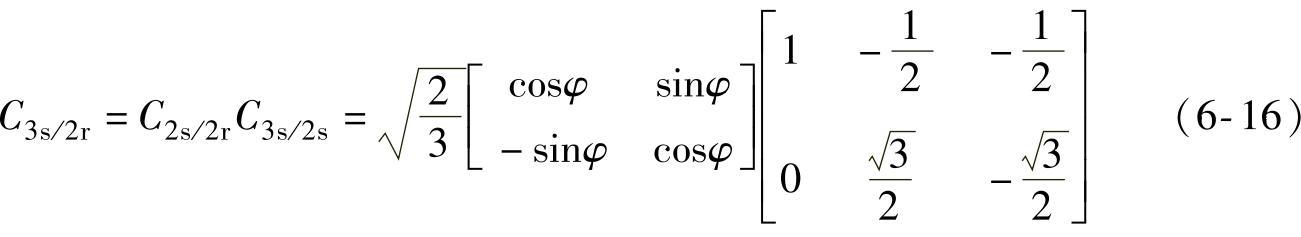
显然有Ψ_r=Ψ_d=Ψ_rm，Ψ_rq=0，如图6-13所示。

基于转子磁场定向控制的感应电机的磁链方程式为

式中T_r为转子时间常数，T_r=L_r/R_r。

基于转子磁场定向控制的感应电机电磁转矩方程为

当转子磁链Ψ_r恒定时，式（6-18）可变为

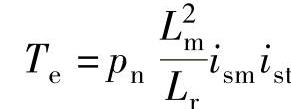
转子磁链恒定时的转矩方程式与直流电机转矩方程式相似，从物理结构上看，感应电机与直流电机不同，不是依靠换向器来固定磁场的空间位置关系，而是通过坐标变换或矢量变换使转子磁链Ψ_r与转矩电流分量i_st正交解耦。因此，可以通过控制Ψ_r和i_st，或控制i_sm和i_st来控制电磁转矩。对于电动汽车驱动电机，在基速以下，保持励磁电流i_sm为额定值，只需调节i_st即可改变电磁转矩，实现转矩控制；在基速以上，调节励磁电流i_sm与转速ω_r自动调节，保持i_smω_r恒定，同时调节转矩电流i_st，保持T_eω_r恒定，实现恒功率控制。

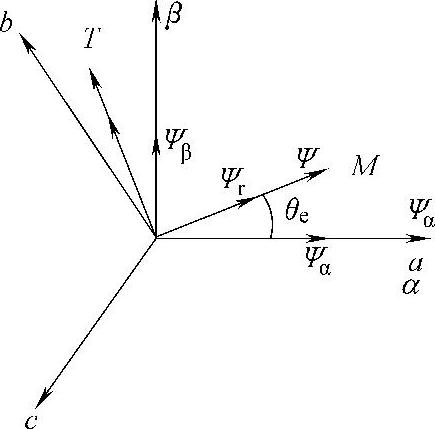
图6-13 磁链转换相图

间接转子磁场定向控制（IRFOC）是基于转子速度和转差速度计算转子磁链位置的一种磁场定向控制方式，是一种比较成熟的感应电机控制算法。在IRFOC控制方式下异步电机控制模型为

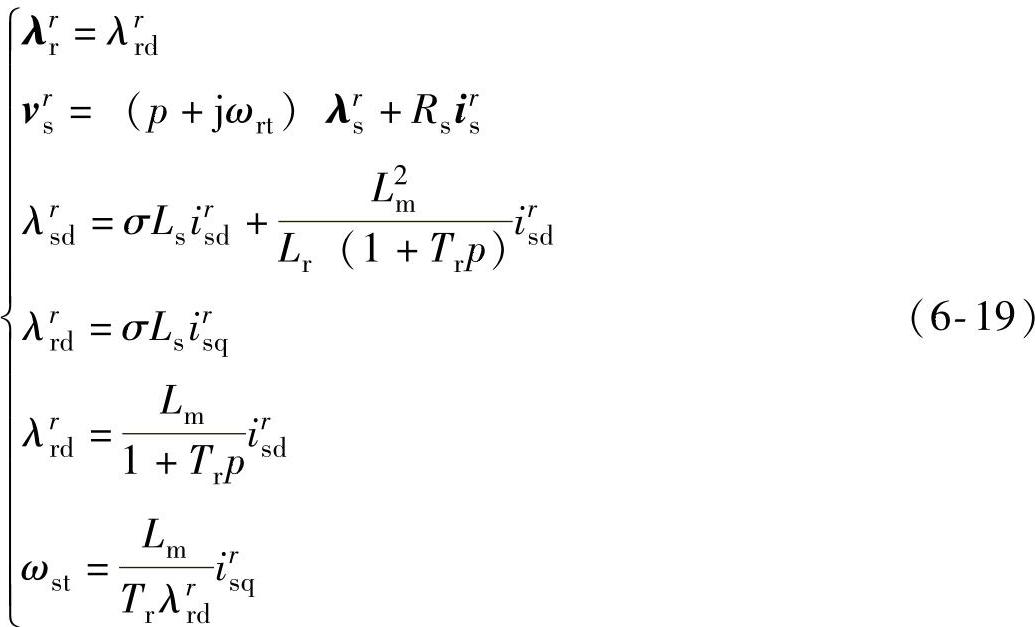
而且，根据式（6-18），得到电磁转矩方程为

如果已知转子速度和转差速度，那么转子磁链位置为

基于IRFOC算法的关键在于PWM的调节方法，一般可以分为CRPWM和SVPWM。前者一般采用电流滞环比较器直接产生PWM，虽然实时性好，但严重依赖控制周期的大小；而后者一般基于PI电流调节器产生电压信号实现PWM。SVPWM比CRPWM更适合于VSI全数字控制感应电机。

2.基于转矩和磁链调节的IRFOC转矩控制

为满足电动汽车实际驾驶需求和动力性能要求，需要对电机驱动控制系统进行转矩控制，驾驶人操纵踏板施加的是转矩信号，控制系统对转矩进行闭环控制。进行电磁转矩控制环和转子磁链控制环的IRFOC矢量控制系统如图6-14所示，下面分别对两个控制环进行分析设计。

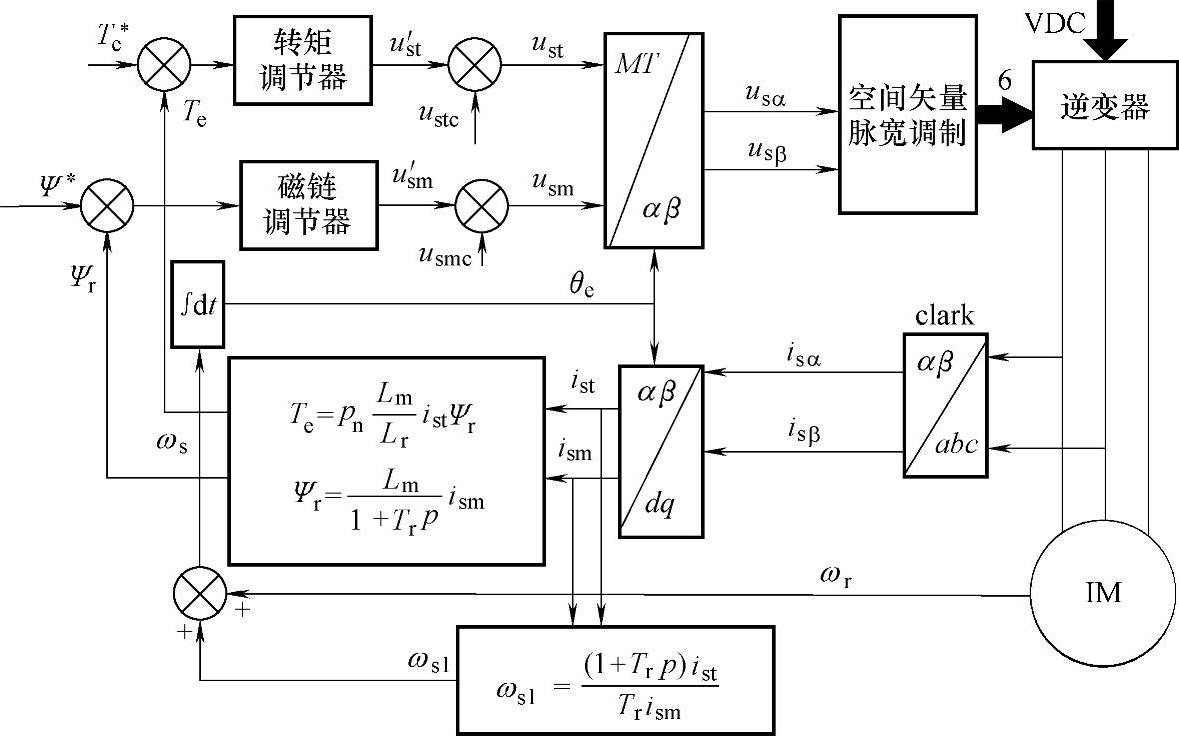
图6-14 IRFOC矢量控制系统

根据IRFOC矢量控制系统中异步电机数学模型有

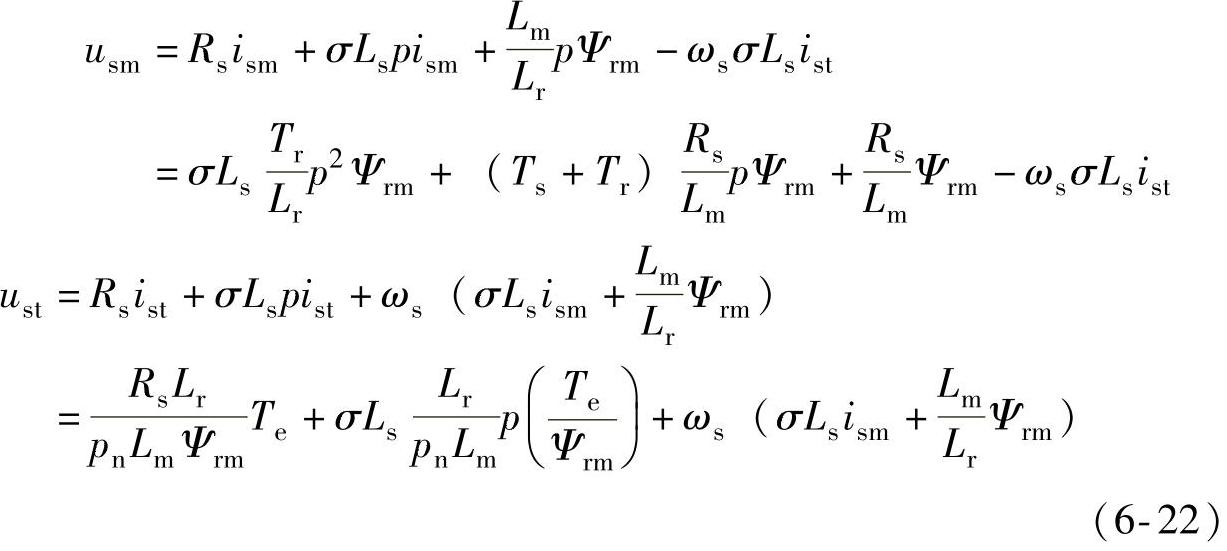
式中， 。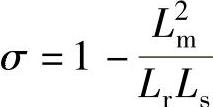

以上两式中含有与ω_s有关的旋转电动势耦合项，若令

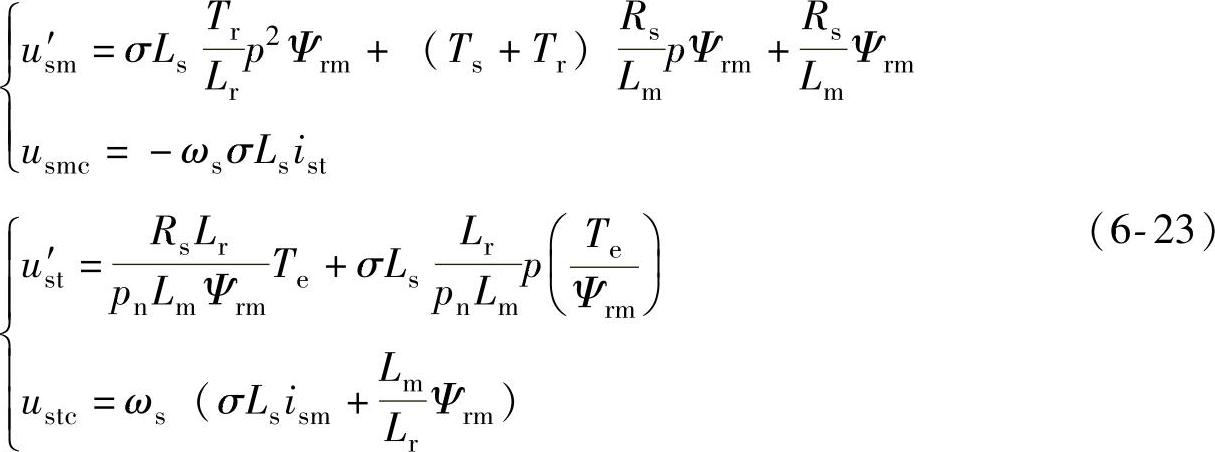
则可得

式中，T_s=L_s/R_s；T_r=L_r/R_r。

（1）磁链控制环的设计

对磁链进行闭环控制，就是为了保证在动态过程中保持磁链恒定。过大超调量容易使磁链饱和，所以要求突加控制量时的超调量要尽量小，即系统要有良好的动态特性。根据式（6-23），将转子磁链Ψ_r和M轴电压u′_sm的关系写成传递函数形式为

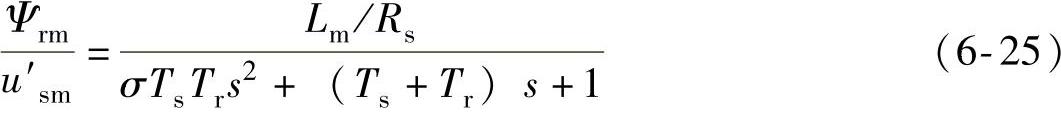
式（6-25）是一个二阶系统，但不是典型的Ⅰ型或Ⅱ型系统。通过根轨迹分析，系统不稳定。为了使系统稳定，提高系统控制精度和响应快速性，磁链控制环串入一个磁链PI调节器，把此系统校正为典型的Ⅰ型系统，如图6-15所示。

图6-15 转子磁链传递函数框图

设PI调节器传递函数为K_p（Ts+1）/Ts，则引入PI调节器的磁链闭环结构图如图6-16所示。

图6-16 引入PI调节器的磁链闭环结构图

对式（6-25）进行分解得到

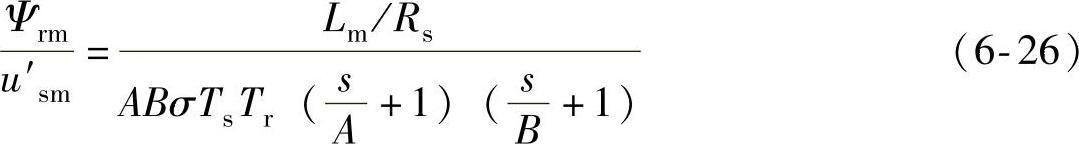
式中，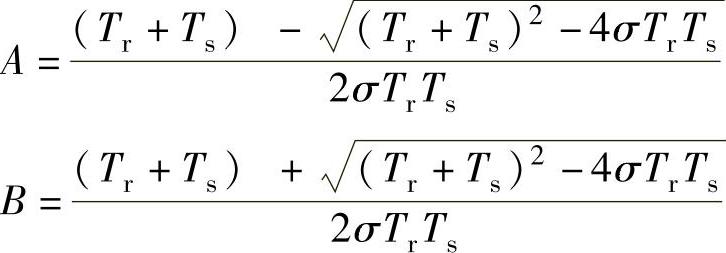

取T=1/A，则可以得到转子磁链环开环传递函数变为

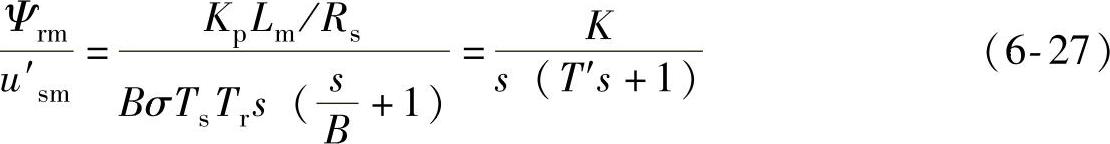(www.daowen.com)

式中， ； 。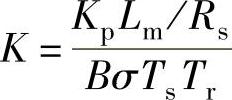

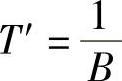式（6-27）是一个典型Ⅰ型系统。根据典型Ⅰ型系统最优动态性能的要求，须满足KT′=0.5，整理得

以上T′、K_p给出的是参数的大致范围，要在实际的系统调试中再对T′、K_p进行微调，直到达到系统的最优点，满足转子磁链性能要求为止。

（2）转矩控制环的设计

根据电动汽车电机驱动控制系统驾驶和动力性能要求，在控制过程中，要求基速以下电机输出最大恒定磁链。由式（6-20）和式（6-21）可得转矩与电压之间的传递函数为

由式（6-29）可以看出转矩信号含有惯性环节，给反馈环节带来延迟，为了平衡这一延迟，在给定信号通道加一个时间常数T_c的一阶惯性环节，则式（6-29）变为

与磁链传递函数类似，式（6-30）是一个二阶系统，但不是典型的Ⅰ型或Ⅱ型系统，因此转矩控制环串入一个转矩PI调节器，把此系统校正为典型的Ⅰ型系统，如图6-17所示。

设PI调节器传递函数为K_p（Ts+1）/Ts，引入PI调节器的转矩闭环结构如图6-18所示。

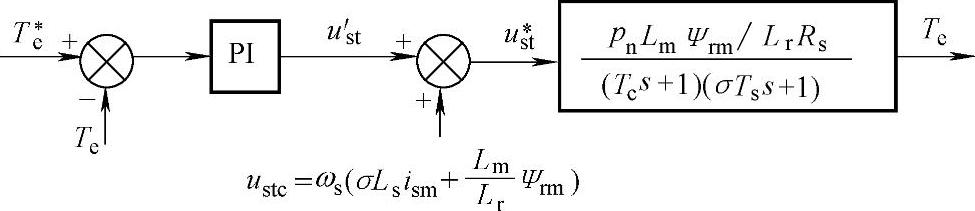
图6-17 转矩传递函数框图（典型Ⅰ型系统）

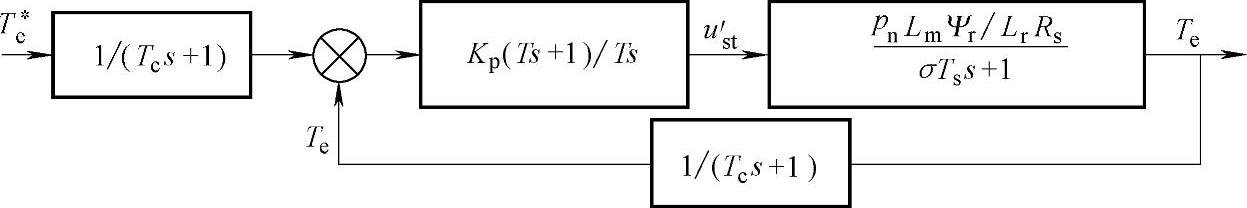
图6-18 引入PI调节器的转矩闭环结构

令T=σT_s，T_c＜T，校正后的转矩开环传递函数为

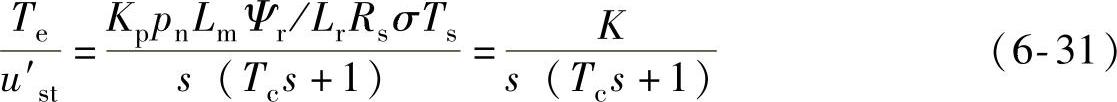
这是一个典型Ⅰ型系统。根据典型Ⅰ型系统最优动态性能的要求，须满足KT_c=0.5，由式（6-31）整理得

与转子磁链调节器参数设计相似，首先确定T、K_p、T_c的大致范围，再在实际的系统调试中对T、K_p、T_c微调，直到达到系统的最优点。

3.基于双PI电流调节的IRFOC转矩控制

由于PID控制是一种负反馈控制，原理简单，使用方便，适应性强，有一定的鲁棒性，因此在工业控制中广泛应用，但是要根据不同的控制要求，试验调整PID调节器系数。异步电机双PI电流调节的转矩控制原理图如图6-19所示。

在d-q坐标系中，建立两个PI电流调节器，分别调节励磁电流分量和转矩电流分量，那么时域误差定义为

双PI调节器为

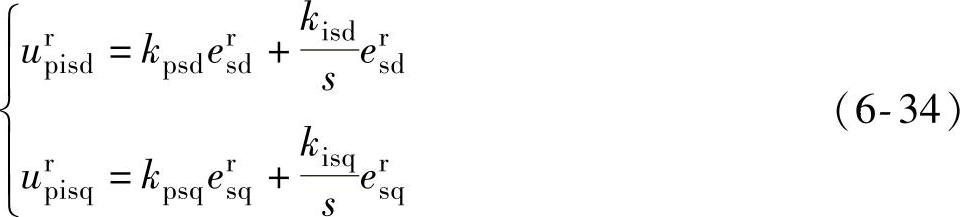
一般来讲，双PI调节器系数相同。

PI电流调节器的矢量控制存在d-q电流耦合效应，因为d-q电流以旋转电动势形式产生d-q耦合。随着转速的提高，d-q的耦合效应越来越明显。

常用的两种PI电流调节器解耦补偿结构如图6-20所示。比较而言，前馈解耦补偿结构简单，计算量小，而反馈积分解耦补偿具有较好的抑制参数扰动能力。

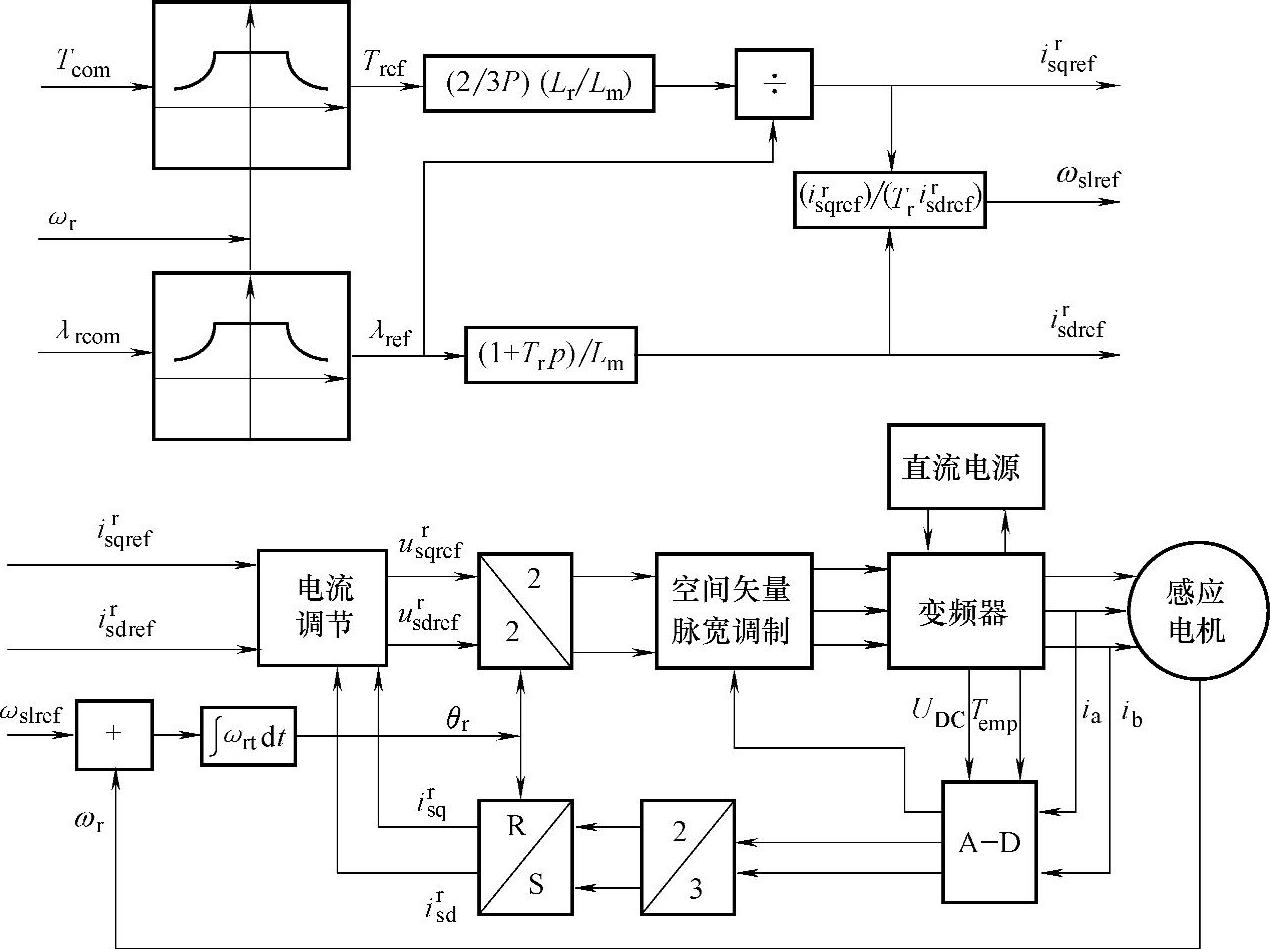
图6-19 异步电机双PI电流调节的转矩控制原理图

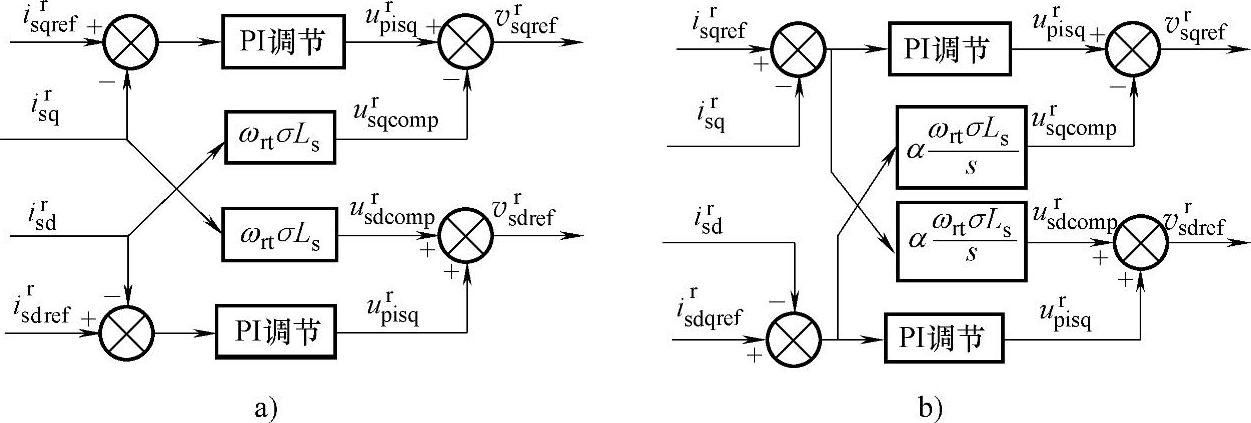
图6-20 PI电流调节器解耦补偿结构

a）前馈解耦补偿 b）反馈积分解耦补偿

4.基于模型转矩反馈速度补偿的IRFOC转矩控制

根据IRFOC的异步电机定子稳态方程式，当异步电机起动时转速为零或很小，模型给定的定子电压几乎为零，使得异步电机不能形成足够的起动电流，为此在异步电机起动时需要一个定子电压补偿量。

根据电机机械运动方程可以推得速度计算式为

这样可以构造一个PI速度补偿调节器，即

式中，k_tp、k_ti均为PI调节器系数；e_t为指定转矩与实际转矩偏差。

通过PI调节器补偿模型起动速度，保证了在零速或低速时IRFOC模型控制异步电机的有效起动，形成模型转矩反馈速度补偿控制算法（MT-IRFOC）。其算法结构如图6-21所示，很显然，MT-IRFOC的实时计算量比PI-IRFOC小，因为只有一个PI计算。

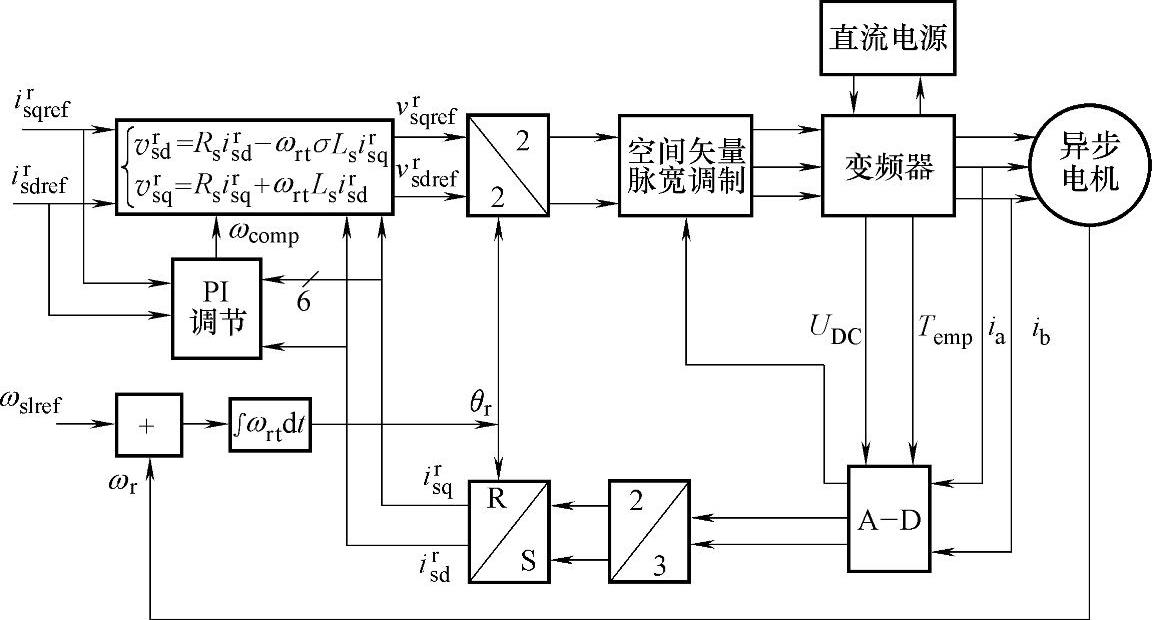
图6-21 基于模型转矩反馈速度补偿算法结构

5.弱磁控制

经典异步电机FOC的弱磁控制给定转子磁链参考与转速成反比，但在整个高速区内并不能获得最大转矩输出能力。当感应电机处于弱磁区时，为了防感应反电动势超过额定电压值，必须对定子电流适当控制，实现对转子磁链调节，稳态的定子电压方程为

忽略定子电阻压降，相应的定子电流约束方程为

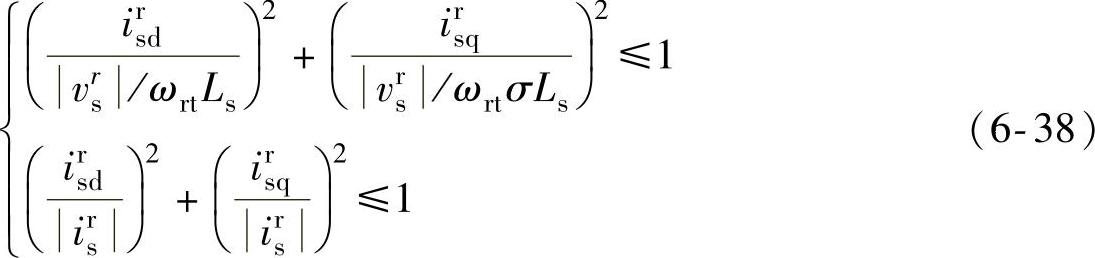
而且弱磁区的电磁转矩可近似表达为