如前所述，评价机构的方式之一便是比较它们的均值。然而，评价方法不应该是平均值的比较，而应该是机构发表的最成功文献的比较。如，机构发表的文献在10%高被引论文中的比例是多少？

同样，这里存在一个很明显的标准：总的来说，我们知道所有文献中的10%排在高被引文献的前10%。本例中我们使用这个标准，但标准的宽严也可根据机构类型做相应的调整。

对二分变量的统计量及显著性检验的计算有很大区别。二分变量不服从正态分布，其平均数及方差也不是彼此独立的。如果平均数Y＝P，那么V（Y）＝P（1-P），例如，如果Y＝1的概率为0.3，那么V（Y）＝0.3×0.7＝0.21。正如Stata 13参考手册（2013）所指出的，提出了许多用于计算可信区间（如Wilson、Agresti、Klopper-Pearson及Jeffries方法）及其他统计量的公式。我们在这里使用Stata's Prtest命令中的大样本方法，但是对于小样本，研究者应探索其他选项。

除此之外，其他参数大体上与前面一样。显著性检验与可信区间的优缺点与此前的情况相似。呈现结果可视化的方式也是相似的。效应量用于说明研究结果的实际意义。简而言之，与之前最大的区别就是用于影响力评估的标准不同。

表12.4列出了各机构的效应量以及与PPtop10%相关的指标。图12.3说明了如何以图形的方式描述比例和可信区间。

表12.4　个体机构PPtop10%的效应量及显著性检验

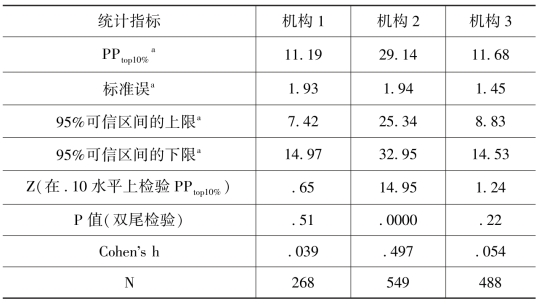
a把数字乘以100转换成百分数。

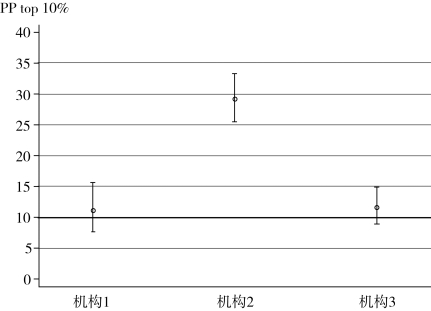
图12.3　各机构的PPtop10%，95%可信区间

注意：我们对二分变量使用Z检验（而不是t检验）。在计算检验统计量时没有使用观测样本的标准差，而是使用了零假设所隐含的标准差。机构2的Z值计算如下：

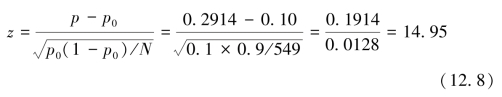
计算结果与我们分析百分位数平均值时的结果非常相似。一方面，机构1和机构3比平均数略高，全部论文中，有略多于11%的论文属于10%高被引论文。相应地，各自的可信区间都包括10，显著性检验证实不能拒绝PPtop10%＝10的零假设。另一方面，机构2发表的文献中属于前10%的高被引论文占其发表的全部论文的29%。可信区间及显著性检验的结果表明如此强的影响力绝非偶然因素可以解释的。

需要注意的是，表中没有Cohen's d值，因为Cohen's d不适用于二分类变量。因此，Cohen（1988）针对二分类变量提出了效应量Cohen's h^[5]。Cohen's h的计算公式不太易于理解，但是有几个不错的性质。h指数计算如下：

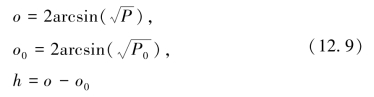(www.daowen.com)

以机构2为例，P＝0.2914（PPtop10%＝29.14）。当P0＝0.10时，机构2的h值为：

根据Cohen（1988）的建议：0.2代表较小效应，0.5代表中等效应，0.8代表较大效应，至少当没有一个合理的指南说明何为较小效果、中等效果和较大效果时，上述原则对于h统计量而言仍是一种合理的选择。他进一步指出，在P0＝0.5的一般案例中，h约等于2（P-0.5）。

表12.5列出了用于机构间比较的相应统计指标。

表12.5　机构间PPtop10%差值效应量及显著性检验

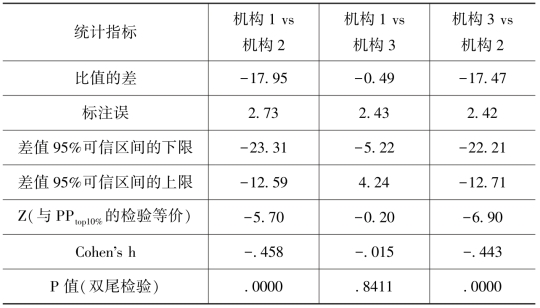
本次结果再一次与之前的结果相一致。机构1和机构3的差别很小，可能只是偶然因素所致。机构2的PPtop10%值是机构1和机构3的两倍多，差别有显著的统计意义。Cohen's h值的计算同前所述，这里把P0换成了P2，以机构1和机构2为例：

人们还提出了另外一些效应量指标，这些指标广泛应用于二分类因变量。这些指标有风险比、比值比、边缘效应。对这些方法的讨论详见Williams（2012）、Bornmann和Williams（2013）、Deschachat以及Engels（见本书）、Long和Freese的论著（2006）。☞

总结

美国心理协会呼吁研究者使用对研究结果的统计意义和实际意义都能给出解释的技术方法。由国际医学期刊编辑委员会（ICMJE，2010）编撰的Uniform Requirements for Manuscript（URM）的统计说明部分同样推荐：“在描述统计方法时要尽量提供详细的信息，以便于专业的读者对原始数据再次计算来验证文献结果的正确性。”如果可能的话，结果要量化并提供关于误差及不确定性的指标（如可信区间）。不要仅仅依赖假设检验等指标，如P值，它无法给出有关效应量的重要信息。

在本章，我们对平均值及比例的效应量分析均是有意义的，但是一定要伴有评估效应量统计意义及实际意义的标准。有关统计显著意义的指标大家都知道，本章我们演示了如何将这些指标应用于文献计量学的数据。对实际意义的判断部分取决于理论或者实验方法：效应量多大时才能认为其很重要？但是，当理论及实验证据不够充分时，像Cohen's h这样的指标就能帮助评估效应量。正如我们所看到的，有统计学意义的效应量可能没有实际意义。相反，可能会有这样的情况：效应量没有统计学意义，但是却有显著的实际意义。使用本书及Cumming（2012）在其著作中提到的工具能帮助研究者评估其研究结果的统计意义及实际意义。

如果有读者想重新演示文章的研究结果或者想用自己的数据尝试，可以参见附录中的Stata代码，附录也提供了证实结果是否有效的检查方法。