与使用一些绝对标准进行评价相比（例如，样本平均值比总体平均数高还是低），我们更希望进行机构间的比较。例如，学校可能希望与其竞争对手或同地区在招生方面有竞争的其他学校作比较。某机构的平均得分比其他机构明显高出很多，还是分数差不多？另外，我们希望对同一家机构在不同时间点作比较，看看随着时间的变化它的平均分是变高了还是低了。表12.3给出了这样的比较。

如表12.3所示，机构1比机构2差17.52分。机构2要比机构3强约14分。机构1和机构3之间的均数相差不多，只有3.69分。

如前所述，简单地比较机构间的均数是不够的。明显的差值可能不具有统计学意义；仅仅是偶然因素便可能使某机构得分高于另一个。即使偶然因素以外的因素也会导致得分的差别，因此我们仍需考虑差别的实际意义。

于是可信区间再次派上用场。翻回去看一下图12.1，可以发现机构间95%的可信区间是否有交集。正如Cumming（2012）所言，如果有交集，则机构间的差别在检验水准为0.01时没有统计学意义。一个常见的错误是：假设两个95%的可信区间有重叠，那么在0.05水平上的差别不具有统计学意义。之所以错误是因为，如果仅是由于偶然因素，则不可能一个变量取非典型低值，而另一个变量取非典型高值。

计算两机构差值的可信区间在这里更是大有用途。如果0在95%的可信区间内，那么两组的差别不具有统计学意义。或者，如果样本差值为10，可信区间为5到15，那么实际的差值最小值可为5，最大值可为15。图12.2较为清晰地给出了解释信息，这些信息在表12.3里也有体现。如果y＝0这条水平线穿过可信区间，那么平均数间的差别就不具有统计学意义。可信区间表明：机构1和机构3之间的差别很微小或者不存在，但是机构2和其他机构的差别（差别在10分或者更大）即便在可信区间的下限也很明显。

显著性检验（本例中是独立性单样本检验）在这里仍然适用。由于是做组间比较，计算过程有些复杂，但仍简单易懂。一般假设两组间的方差相同^[4]，但在本样本中，对各组方差进行了分别估计。

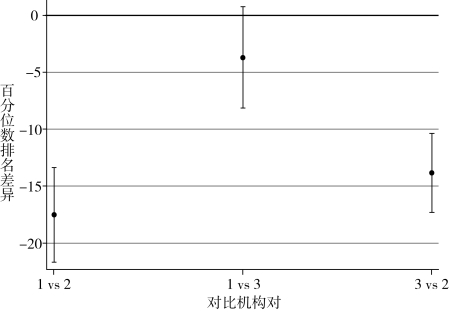
图12.2　平均百分位数的差异，95%可信区间

两组间方差的合并估计如下（先列出一般公式，然后以机构1和机构2为例详细计算）：差异的标准误（同样，先列出一般公式，然后以机构1和机构2为例详细计算）为：

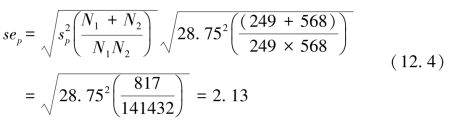(www.daowen.com)

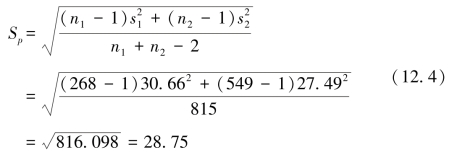
t检验（同样，先列出一般公式，然后以机构1和机构2为例详细计算）为：

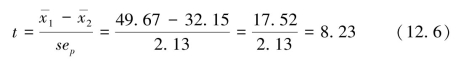
检验结果证实机构2比其他两个机构的得分要高，并且差别有统计学意义，机构1和机构3的差别很小，可能只能归因于偶然因素。

如前所述，当质疑（例如变量服从正态分布）参数假设的有效性时可使用Bootstrapping技术，经Bootstrapping得到的结果与表12.3的结果非常接近。我们使用Mann-Whitney检验对表12.3的数据进行额外的检查。当因变量是序级测量而非区间测量时，比较适合使用Mann-Whitney检验（Acock，2010），而百分位数排名显然至少是序级测量。Mann-Whitney检验与表中t检验的统计量结果基本一致，再次增加了我们对结果有效性的信心。进一步分析发现，表12.3所使用的方法要优于非参数检验（如Mann-Whitney检验等），因为Cohen's d和可信区间等统计量可被估计和解释，方便对研究结果的实际意义的理解。

显著性检验（t检验或Mann-Whitney检验）有着与前文所述相类似的问题。如果样本量足够大，即使很小的差别也有统计学意义，例如，如果样本量足够大，仅仅1分的差别也有统计学意义。相反，如果样本量很小，即使差别很大（如10分的差别），在0.05的水平上也不会有统计学意义。

为了更好地评估实际差异，可使用Cohen's d计算均值之间的差异。公式如下（先列出一般公式，然后以机构1和机构2为例详细计算）：

Cohen's d值说明：机构2和机构1的差别（.613）以及机构2和机构3的差异（.487）至少是适中的。相反，机构1和机构3之间差别的Cohen's d值0.124低于Cohen给出的代表较小效应的界限值。