表12.2中列出了每个机构的Cohen's d值。Cohen's d及其他相关测量指标（如下文的Cohen's h）试图阐述效应量的级别。换言之，这些指标试着阐述结果的实际重要性，而非统计重要性。当对效应量的大小不得而知时，Cohen's d及其他相关指标便显得尤其有用。举个例子，如果某机构得分比平均值高3分，到底得分差异的实际意义是大，还是小呢？

那些对某一领域非常了解的专业人士，可能对此给出有依据的观点。但是对某领域知之甚少的时候，Cohen's d在评估结果的实际意义时有着潜在的优势，而不是简单地注意观察的差值为多少。正如Cumming（2012）所言，Cohen's d能帮助更多的读者理解效应量，尤其当人们对首次用于测量效应量的单位不熟悉时。Cumming（2012）还说过，Cohen's d也可用于Meta分析，在Meta分析中对不同研究者使用不同方法测量关键变量。

在单样本案例中，样本均值与假设均值的差值除以样本标准差即为Cohen's d值，计算公式如下：

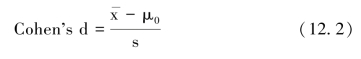
经过简单的计算，可得出。例如，机构2的Cohen's d值为：

Cohen（1988）说过，Cohen's d与z-score转换相似。如果Cohen's d值为0.2，意味着样本均数比假设的总体均数高0.2个标准差。Cohen（1988）建议效应量为0.2、0.5和0.8（或者当编码相反时，为-0.2、-0.5和-0.8），分别对应较小效应、中等效应和较大效应。

换言之，Cohen's d指标有用与否部分取决于“意义”的观测差异有多明显。例如，实验教学组学生的成绩比传统教学组学生的成绩高出一个等级，这样的差距人们一看就知道有意义。但是，如果在一些标准化测试中，实验组的成绩高出7分，只有用Cohen's d才能帮助判断两组成绩的差距到底有多大^[3]。

我们再回过头看一下表12.2中的3个机构，机构1的Cohen's d值极小，几乎为0。尽管机构3的样本均数和总体均数50的差别有统计学意义，但是Cohen's d值只有-0.137，比Cohen（1988）建议的代表较小效应的-0.2要小。机构2的Cohen's d值为-0.649，这个值介于代表中等效应的Cohen值-0.5及代表较大效应的-0.8之间。(www.daowen.com)

表12.3　机构间百分位数差别的效应量及显著性检验

续表

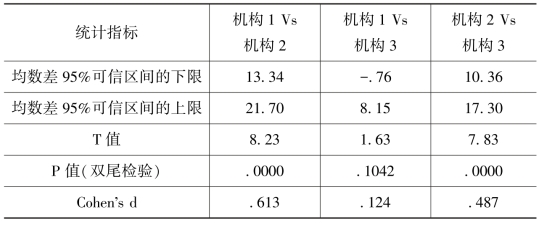
因此，在没有其他可用的标准来评估效应量级时，Cohen's d值可让我们得出如下结论：机构1、机构3及总体均值50之间的差异没有实际意义，而相对而言机构2和总体均值间的差别有较大的实际意义。

在表12.2中，我们还做了一些额外的分析来证实结果的有效性。在表12.2（以及表12.3）中，我们使用了大量的t检验及相关统计量。正如Acock（2010）指出的那样，t检验假设变量服从正态分布，并且当两组数据进行比较时，通常假设组间方差是相同的。而百分位数由于不是正态分布，所以不满足这些假设。然而，Acock（2010）进一步指出在不满足假设的情况下t检验仍表现得很好。

虽然如此，为了确保结果的有效性，我们使用常用的校正技术再次检查了计算结果，这些技术在正态分布假设不满足的条件下也非常有效。对于表12.2和表12.3，我们使用了Bootstrapping技术来确保结果的有效性。当对假设有疑问时，可使用Bootstrapping技术进行基于参数假设的推理（Cameron，Trivedi，2010）。Bootstrapping对观察对象进行多次抽样。通过多次取样，可估计标准误、可信区间及显著性检验。经Bootstrapping得到的显著性检验及可信区间几乎与表中报告的结果一样，这让我们对于结果的有效性更加有信心了。