现在我们将展现如何通过统计学软件Stata得到我们的结果。

对二分变量Logit模型进行评估，其中，虚拟变量“D-cited”表示论文被引用的结果，JASIST（第二期刊）为参照类别：

logit D_cited ib2.Journal NumAut NumCoun NumRef NumPag NumTitle i.First i.Fund PubYear PubMon i.H i.InnoPat.

二分变量Logit模型的预测表、调整后的数值R2、比值比以及对均值处的边际效应可由如下方式获得：

estat classification

fitstat

logit D_cited ib2.Journal NumAut NumCoun NumRef NumPag NumTitle i.

First i.Fund PubYear PubMon i.H i.InnoPat，ormargins，dydx(*)atmeans

为了减少估计其他模型所需的代码，我们先定义一些自变量，我们称其为“indeps”：

local indeps JOI SM RP RE NumAut NumCoun NumRef NumPag NumTitle First Fund PubYear PubMon H InnoPat

在有序Logit模型中对系数和比值比进行估计，其中类别变量“引文类别”包括三种分类：

ologit citation_categories‘indeps’

ologit citation_categories‘indeps’，or

brant，detail

计数变量“citation”的泊松、准泊松以及负二项模型可以通过如下方式得到^[10]：

poisson citations‘indeps’

glm citations‘indeps’，family(poisson)link(log)scale(x2)(www.daowen.com)

nbreg citations‘indeps’☞

总结

分类变量或频次计数变量在信息计量学中非常普遍。本章对可用来分析上述数据的受限因变量回归模型进行了介绍和对比分析。线性模型的使用往往在信息计量学中并不合理，因为其中潜在的一些假设并不适用于信息计量数据集（Leydesdorff，Bensman，2006）。对于研究者们来说，一个现实的问题就是确定哪些受限变量模型及其变型是最适合的。在许多情况下，数据的性质会决定模型的选择（例如，如果结果变量为二分类，那么只能选择二分变量模型）。然而，有时数据会提供不同的模型选择，本章中对论文引文量的分析便是这种情况。在这样的情形下，研究者可通过避免将观察值分为更宽泛的类别，尽力挖掘数据的信息和变化。不过，我们也可能有理由在那些情况下使用分类模型进行估计（例如，汇总分类可能对于特定的研究问题而言更为适合）。在这样的情况下，对不同模型进行评估与比较便具有指导意义。例如，Yoshiikane（2013）采用线性模型、Logistic模型以及零膨胀负二项模型来分析专利引用频次；Niu和Hemminger（2012）在分析信息搜寻行为时采用了一个泊松模型和两个Logistics模型。选择不同的模型是检验一项研究中主要结果的健壮性的一种方法，同时也能够检测数据中存在的有趣的异常现象。

在此要感谢Fereshteh Didegah、Raf Guns、Edward Omey和Ronald Rousseau对本章内容提出的宝贵建议。感谢Richard Williams和Paul J.Wilson的反馈和宝贵建议。

【注释】

[1]N.Deschacht，Faculty of Economics and Business，KU Leuven，Campus Brussel，Warmoesberg 26，1000 Brussel，Belgium，E-mail：Nick.Deschacht＠kuleuven.be；T.C.E.Engels，Department of Research Affairs and Centre for Research＆Development Monitoring(ECOOM)，University of Antwerp，Middelheimlaan 1，2020 Antwerp，Belgium，Antwerp Maritime Academy，Noordkasteel-Oost 6，2030 Antwerp，Belgium E-mail：Tim.Engels＠uantwerpen.be.

[2]如果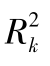是线性回归模型（Xk。是其他解释变量的方程）的决定系数，则方差膨胀因子

[3]除了均值处边际效应，其他方法也可以计算边际效应。如果想了解这方面的讨论和文献计量数据的例子，请参考Bornmann和Williams的研究（2013）。

[4]另一种质量建模的手段为Ajusted Count R2，它同样是基于预测表并且取值在0～100%，参见Long和Freese（2006）。

[5]系数前面的负号是需要的，这是因为累积概率是使用＜＝符号，而系数应当估计解释变量对因变量增长水平的影响。

[6]这种解释只是接近于正确，因为它是从求ln（E[yi｜x1i，…，xki]）关于xi的微分中得出的。

[7]准泊松模型假设Var[yi]＝φ2·E[yi]。其中φ为过度分散系数。φ2的一个估计值为。准泊松系数的标准误可通过泊松MLE的标准误与相乘得到。

[8]利用Generalized Negative Binomial Regression可进一步提高拟合度，它以过度分散系数建模（见Stata中的gnbreg命令）。

[9]AIC＝-2 ln（likelihood）＋2k，其中k是模型中估计系数的数量。所以应选择AIC值较小的模型。与R2不同，AIC是一种相对指标，并且只有在同一数据上比较模型时才有用。

[10]这些模型是一般模型Generalized Linear Model（GLM）的一部分。准泊松模型在Stata中以GLM进行估计，其中使用模型观测和预测值的Pearson卡方值（即在前面讨论过的过度分散系数的估计值φ）对标准误进行了调整（Scaled）。