当变量用于衡量一个事件的频率时，计数资料模型（而不是有序数据模型）更适合于充分利用该数据的基本性质。分析计数资料的标准回归模型为Possion模型，但是在大多数实际应用中需要这种模型的拓展版本（准泊松分布和负二项模型）来克服潜在假设不满足的情况（下文将讨论）。

Abbasi、Altmann、Hossain（2011）应用泊松模型来识别合著网络对学者科研能力的影响。Niu、Hemminger（2012）通过泊松回归实施了信息搜寻行为的Logistic分析。负二项回归模型已经被用于论文数量的建模（Barjak，Robinson，2007；Gantman，2012）和引文量研究，例如比较一系列的论文（Bornmann，Daniel，2006，2008）或作者和期刊的相对重要性（Walters，2006）。Lee，Y.G.、Lee，J.D.、Song，Y.I.、Lee，S.J.（2007）率先在信息计量学中使用零膨胀负二项分布分析韩国科学技术研究所的专利引文量。零膨胀模型有两部分：利用二分类模型预测组别的归属，在后一组数据中使用计数模型（Hoekman，Frenken，van Oort，2009；Long，Freese，2006）。最近，Chen（2012）、Didegah、Thelwall（2013a）和Yoshikane（2013）在他们各自的研究中都运用了零膨胀负二项模型，预测结构变异对引文量的影响，分析纳米科学领域中引文影响力以及日本专利的引文量。零膨胀模型假设有两个来源，故导致零点的原因也有所不同：通过结构性因素解释零观测值的Perfect zero（如新人的人均学术论文数量）和在计量分布中出现的零点值（如一些学者在一段时间内没有论文）。正如Didegah和Thelwall（2013b）所描述的，Hurdle模型可能是一个不错的选择，至少对于引文量分析是这样的。对一篇文献而言，其第一次引用可以视为一个真正的门槛Hurdle，此后其被再次引用的可能性增加。下面我们仅对标准负二项回归作出解释，如果读者对截断模型或其他拓展模式感兴趣的话，可以参考Hilbe（2011）的研究。

（1）泊松、准泊松和负二项回归模型。

如果yi是计数资料，只能取非负整数值（yi＝0，1，2，…），我们假设yi在解释变量的取值上的条件概率服从泊松分布。

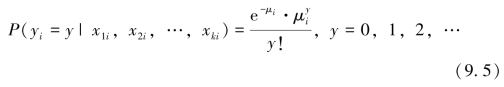
这里的μi是此分布的期望值，注意假设是指yi的条件分布，而不是yi非条件分布。因为后者还由解释变量的分布决定，故观察值yi的分布并不是该模型优于其他模型的有效证据。下面的例证清晰地表明了这一点：在仅有一个二分类解释变量的模型中，其条件分布为泊松分布，而非条件观察值yi通常服从双峰分布（与泊松分布明显不同）。

期望值μi通常采用下面的模型：

由于一些技术性原因，我们估计泊松（以及负二项）模型条件均值的对数，而非均值本身。由此，泊松回归分布可定义为：

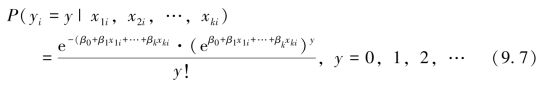
其中各系数用最大似然法进行估计。如果我们将所需值写为如下形式，就可以很明白地解释这些系数。

这是一种类似于线性回归的半对数模型。βi的意义是在其他变量保持不变的条件下，当xi增加一个单位时，μi的相对（百分比）增量^[6]。

泊松回归分布模型的局限在于：任一泊松分布都完全由均值确定，且假设方差与平均值相等（等分散假设）。这种限制条件在许多应用中并不成立，因为方差通常会大于平均值。在这样的情况下存在过度分散，意思就是其方差大于由泊松分布所假设的方差。然而，不管实际条件分布如何，最大似然估计总能为系数给出一致的估计（Wooldridge，1997）。在没有假设泊松分布的情况下使用泊松最大似然估计是正确的，这被称为准泊松模型或泊松QMLE（准最大似然估算法）。在过度分散情况下，泊松分布中系数的标准误会被低估，因而增加了Ⅰ型错误的危险（即错误地认为影响是显著的）。准泊松模型通过估计模型中一个附加参数来调整标准误（准泊松模型假设方差是均值的固定倍数）^[7]。泊松与准泊松模型通常会得到相同的估计系数。

在过度分散的情形中，另外一种可能性是估算负二项回归模型。通过估算一个附加参数（分散参数α），该模型也允许条件均值yi（μi）与其方差不同。因为负二项模型假定方差是其平均值二次函数，因而此模型所允许的均值估计的变异程度远大于准泊松模型^[8]。当α为0时，泊松模型可以看作是负二项模型的特殊情况。由此，对α的显著性检验可以看作是对泊松模型中是否存在过度分散的检验。负二项分布的概率质量函数不同于泊松分布，因而其系数估计，不像在拟泊松分布模型中那样，与在泊松分布模型中的估计不相同，尽管它们似乎很相似。

通常，计数资料回归模型的拟合优度——准R2是通过观测数据yi与模型的预测值的相关性的平方来进行计算。当模型被用作预测时，该R2是该模型（内在）有效性的指标。另外一种衡量方式是Akaike Information Criterion（AIC），它通过对模型估计参数的数量加以惩罚，从而达到拟合度与模型复杂性之间的权衡^[9]。(www.daowen.com)

（2）阐述。

现在我们使用泊松回归模型分析期刊文献在出版一年后的引文量。图9.1展示了样本数据集的2271篇论文引文量的分布情况。

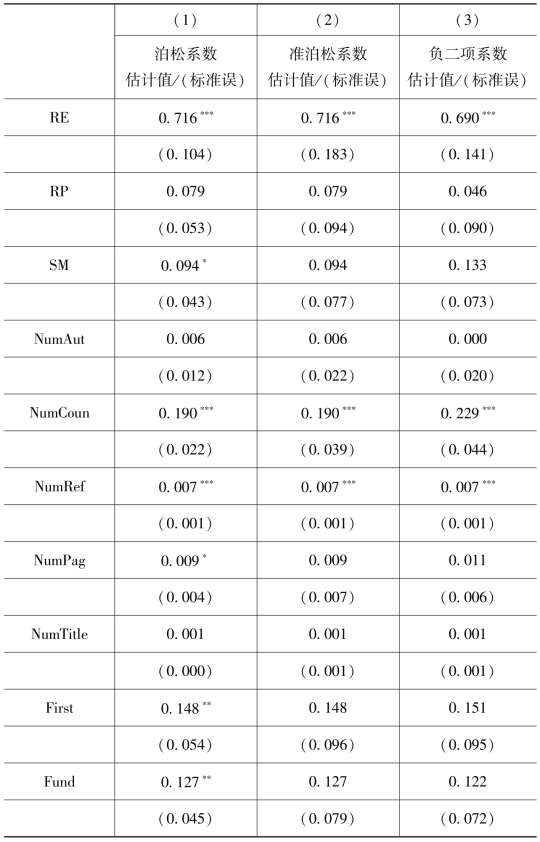
在此分布中，引文量的平均值为1.94，而方差为7.38。这说明泊松回归模型中可能存在过度分散，因此需要考虑替代方法。表9.5中列出了泊松、准泊松模型和负二项回归模型的系数估计。

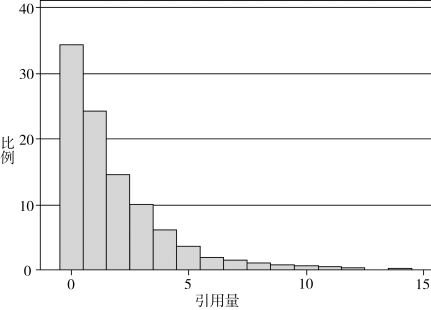
图9.1　引文量的频次分布情况

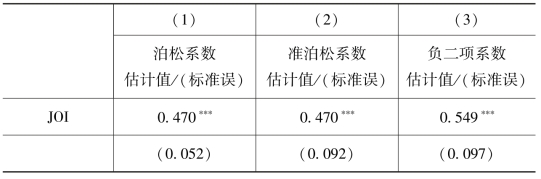
在泊松模型中，JOI的估计的系数为0.47，这表明在其他变量保持不变的条件下，JOI论文的预测引用量比JASIST论文高47%。有关h指数的论文的引文量较其他主题论文多66%。需要注意的是准泊松模型中的系数估计与泊松模型中的相同，可以预期，准泊松模型中的标准误远大于泊松模型。事实上这个差距是77%，因为过度分散的统计值是ψ＝1.77（没在表中显示）。这表明泊松分布的假设不能成立，因而其不可用于推论。例如，判定变量“First”的影响具有显著性是错误的，这是因为泊松分布中的这个结果是基于低估的标准误产生的。准泊松模型的显著性检验表明在JOI中发表论文对其被引量有正面影响，而在RE发表论文对其被引量则有负面影响（相对于JASIST中的论文而言）。我们还发现国际合作、参考文献引用数量、有关h指数的论文以及出版月份这几个控制变量对于论文的引用量也存在显著的正面影响。负二项模型的结果同准泊松模型的结果非常相似：相同的影响在同一显著性水平是显著的，且具有非常相似的估计效应量。例如，有关h指数论文的引文量的期望值比其他论文高70%，而增加一篇参考文献的影响为0.7%。因而增加100篇参考文献所产生的影响同转为与h指数相关的主题所产生的影响是相同的。这也说明了h-bubble的影响（Rousseau et al.，2013）。分散参数α的估计值是0.88，这表明存在过度分散。在似然比检验中，将负二项模型与α为0时的泊松模型进行比较，可以确认过度分散参数具有统计学意义（χ2＝1544，p＜0.001），因此泊松模型并不适用而应采用准泊松模型或负二项模型。

为了计算拟合优度，我们计算了引文数量的观察值同准泊松模型（r＝0.300）以及负二项模型（r＝0.290）中预测值之间的Pearson相关系数，得到的准R2结果分别为0.09和0.08。另一方面，AIC在负二项模型中的值较小，因而此模型的拟合度更好。

表9.5　计数资料模型

续表

续表

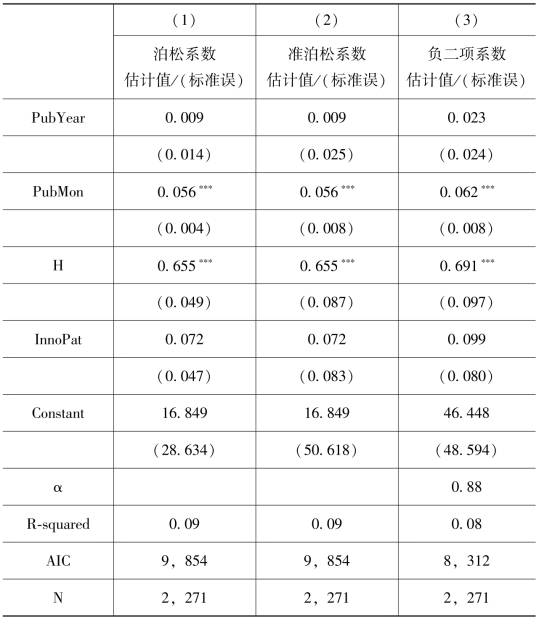
*p＜0.05；**p＜0.01；***p＜0.001

在计数资料模型中发现的效应与之前在分类模型（二分类变量和有序变量）中发现的效应基本上是相同的。这表明分析的主要结果并不受模型改变的影响。然而，尽管结果非常健壮，但每一种方法都确实能够为结果提供额外的见解，而这些见解在仅使用一种方法时往往可能被忽略。例如，对于解释变量“First”，即表示文献是否第一次发表在期刊上，在有序变量模型中确实会对论文的被引量产生显著的影响，然而在二分变量模型或是计数资料模型中却没有这种效应。就期刊的影响效应而言，无论是对于JOI还是RE，从每种模型中都可以得到相似的结论（与JASIST相比，前者会产生较高的引文影响，而后者则会产生较低的引文影响）。然而对于RP以及SM，通过比较其与JASIST中论文的引文影响力，不同模型的结果会有一些细微的差别。