在用二分变量回归模型对引用情况进行分析时，所有的被引论文归为一组（样本数据的66%）。然而，被引量少的论文和被引量多的论文之间的区别可能会很大。由于没有利用这一信息，二分类变量回归模型性能降低，增大了Ⅱ型错误。当因变量是一个有序变量时，用有序变量回归模型比较合适。

近年来，在文献计量学和信息计量学研究领域，分类或有序Logistic模型的应用案例包括分析和预测学术研究者信息搜寻行为的影响因素（Niu，Hemminger，2012），国际间合作对引文影响力的作用（Sin，2011），对科研团队的同行评议（Engels，Goos，Dexters，Spruyt，2013）。以及推特中出现的“＃”号标签的受欢迎程度（Ma，Sun，Cong，2013）等。其他可用有序变量模型分析的案例包括期刊投稿论文的同行评议结果（包括录用、小修、大修及拒稿）和教授的头衔（助理教授、副教授、全职教授）。有些情况下，如研究项目的发表成果（仅学术论文，仅专利，学术论文＋专利，学术论文＋受欢迎的论文等），其分类并不是严格的有序变量。在这种情况下，可以用多项Logit模型来分析数据。

（1）有序变量Logit模型。

如果yi是有序变量，取值为j＝1，2，…，J，其累积概率为观察值i在第j类或更低类别中概率的总和：

有序变量Logit模型的定义为

对于不同类别的j值，有不同的截距aj，并假设随着类别的变化斜率系数是不变的^[5]。βi是指在其他变量不变的情况下，xi每增加一个单位，文献属于更高类别时log-odds的增加量。与二分类模型一样，比值比eβi是指随着xi增加1个单位，文献属于更高类别所增加的几率。

在有序Logit模型中，假定每一个类别斜率系数相等，这个“proportional odds assumption比率成比例假定”可以通过Brant检验来评估，该检验会计算斜率系数在各二分类变量模型中是否相等。当检验结果不支持假设时，则会考虑其他模型，在这些模型中允许系数在不同类别中变化，例如多项Logit模型。

（2）阐述。

现在我们使用有序Logit模型来研究期刊论文引用量的决定因素。在分析过程中发现，因变量是一个有序变量，可以分为三类：第一类，发表之后未被引用；第二类，发表之后很少被引用（仅被引用1次或2次）；第三类，发表之后被引较多（3次以上）。信息计量学这一领域的2271篇文献中，34%没有被引用，39%的文献只有1～2次被引量，27%的文献被引量大于3次。表9.3显示了被估计的有序变量的模型。

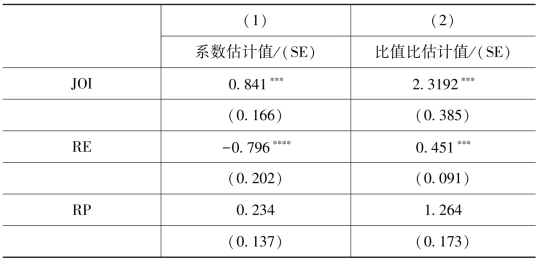
表9.3　有序变量Logit模型

(www.daowen.com)

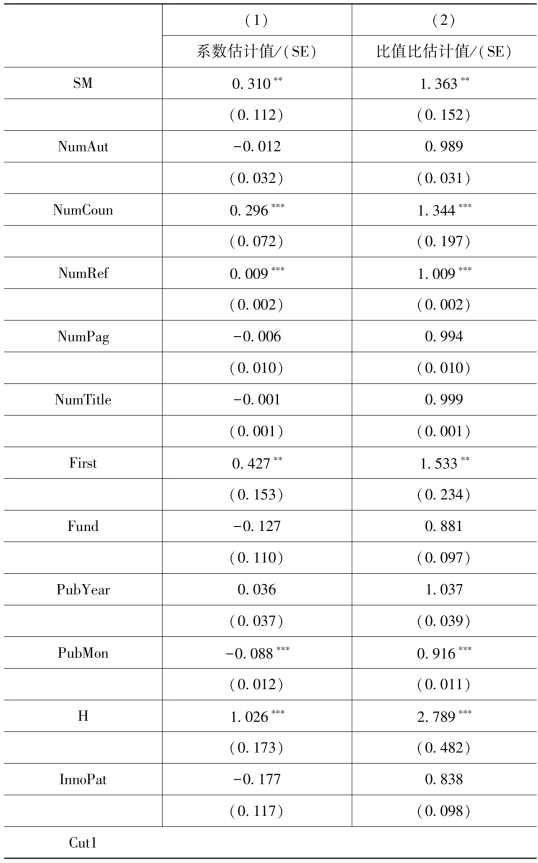
续表

续表

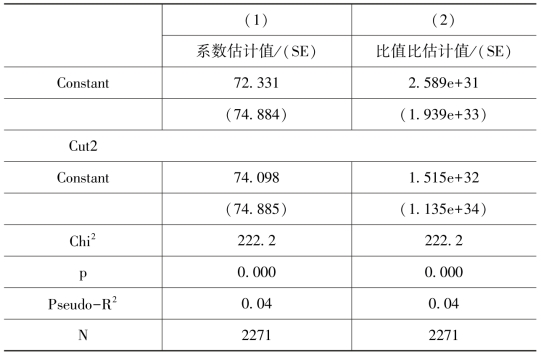
*p＜0.05；**p＜0.01；***p＜0.001

JOI的比值比是2.3，表明在其他条件不变的情况下，JOI中文献属于更高类别的几率要比JASIST中的文献高2.3倍。将这些结果与二分类变量模型中的计算结果进行对比后发现，许多系数都有较小的p值，这表明将论文按照被引频次的高低区分后，模型的性能得以提高。例如，国际合作这一变量的系数在此模型中具有显著的统计学意义（p＜0.0001，在二分类变量模型中p＝0.035）。用于表明论文是否为本期第一篇论文的虚拟变量在此模型中也有统计学意义（p＝0.005），而在二分类变量模型中却显示无意义（p＝0.135）。进一步分析可以发现其原因是：虽然首篇文献与其他文献相比未被引用的概率是相似的，但它们获得较多被引量的概率却很大。这种情况违背了有序Logit模型的潜在条件，即比率成比例假定（对无被引和有被引比率的影响与对低被引和高被引的比率的影响是不同的）。这里有一个变量的情况与上一个模型相反：在有序变量模型中，是否为RP期刊发表的文献这一指标不再有统计学意义。原因是与JASIST类别中的文献相比，RP期刊中有很大一部分论文没有被引用（在二分类变量模型中产生了影响），然而同时在RP期刊中有相当一部分文献的引用量很高（消除了有序模型中的影响）。

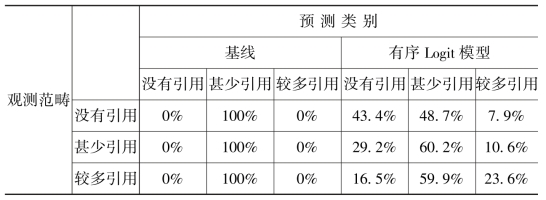
估计好的有序Logit模型现在可以用来计算每一类别的预测积累概率。因为割点会随着类别水平的增加而增加，所以累积概率随之增加。相邻两个累积概率之间的差异生成每一种类别的预测概率。如果我们以使用最大预测概率预测类别作为决策规则，则该模型在预测无被引论文时的正确率为43%，预测低被引论文时的正确率为60%，预测高被引论文时的正确率为24%（见表9.4）。

无解释变量的基线模型会为每一篇文献预测一些被引量，因为那是总体比例最大的种类（占38%）。表9.4显示有序Logit模型中对角线元素的总和为127.2%，大于基线模型对角线元素的总和（通常为100%），这是任何评估模型最低质量的要求。

表9.4　有序变量Logit模型预测表

Brant检验计算“比率成比例假设”所得的结果为χ2＝23.5（p＝0.07），如果p＞0.05，则表明该比率成比例假设的反对证据没有统计学意义。值得注意的一点是，显著性检验与样本是相关的，在该例证中意味着，如果样本量很大（在小样本中较大的差异也可能没有统计学意义），即使斜率系数有很小的差异也会导致拒绝无效假设。因为我们的p值与显著性水平相比并没有高出很多，因此我们还使用多项Logit模型进行了估计，此模型由多个二分类模型组成，因此斜率系数允许变化（没有报告具体参数和估计值）。此模型中，对角线元素的和增加至131.8%。然而，预测力的这一点增加需要模型使用更多的参数进行估计，而这将增加过度拟合的风险。虽然有序模型和多项模型都有自身的优点，但是由于此例中该模型的简约性以及比率成比例假设的可能性，作者偏向于使用有序模型。在比率成比例假设明显不成立，以及非有序因变量的情况下，使用多项模型更为合适。