我们先关注合作者网络。依据合作者关系这种协作的最可见表现形式，这些网络已经被广泛用于研究科学中的协作。虽然这个假设有自身的问题，但详细讨论协作网络超出本章的范围。近来关注合作者网络的文章有：Mali，Kronegger，Doreian，Ferligoj（2012）和Biancani，McFarland（2013）。

在数据集中有2294个作者和3687个链接。网络相对稀疏，密度为0.001。平均节点度为3.2。但是，7.8%的作者在那段时间没有合作过。协作者最多（值为40）的作者是Glänzel。请注意，我们使用“协作者”（Collaborators）一词来表示一个给定作者在一段时期内合作写过文章的全部作者（或者，更精确地说，清楚的作者名字），而“合作者”（Coauthors）一词用于表示在一篇文章中出现的作者。

协作者数量的分布是一个作者网络结构和形成此结构的过程的重要指标。因为在合作者网络中，每位作者拥有的协作者数量是一个节点的度，所以协作者数量分布和节点度分布一样。网络中的度分布通常是右偏的（意味着大部分节点的度低于平均值，一小部分中心节点的度是平均值的几倍），是无标度网络，至少在尾部服从幂率函数（Börner et al.，2007；Newman，2003；Watts，2004）。事实是无标度本身就是一种指标，少量的“明星”（Stars）（拥有大量链接）负责连接整个网络。

为了在Pajek中获得度分布，可以点击Network＞Create Partition＞Degree。对无向网络选择All。对有向网络，如果你对入度感兴趣就选Input，如果你对出度感兴趣则选Output（见图3.8）。

一旦Pajek已计算好度分布，你会在Partitions行看到一个新文件（见图3.9）。想要获得数据就在Partitions下点击i按钮，或者点击Partition＞Info并在弹出窗口保留默认选项。

图3.8　在Pajek中计算无向网络的度分布

图3.9　计算度分布后的结果

Report窗口（见图3.10）列出了度频率分布表。但是，如果想要以图形方式展示，就需要一个其他程序，如Excel。如果列表不长，可以在Excel中键入值，然后生成图表。如果列表长，或者想要更从容地处理，就应该通过点击Partitions下的第二个按钮（Save）来保存值，并选择保存为Pajek分区的.clu格式选项。一旦在Excel导入此文件，就得到只有一列的度值。这是一个度值列表，而不是它们的频率。我们需要计算频率然后生成图表。

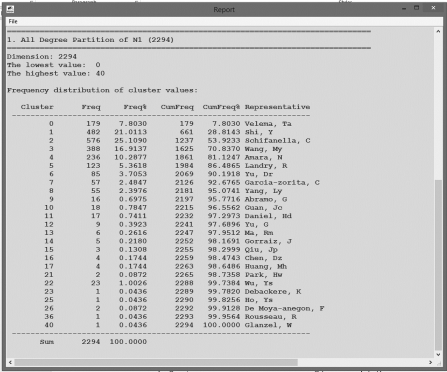
图3.10　Pajek节点度频率分布的报告

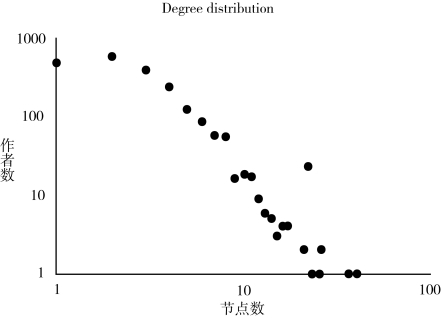
图3.11　2003—2012年《科学计量学》期刊上发表文章的作者的节点度分布

例子中的节点度分布（见图3.11）和文献中大量协作者分布是一样的（Barabási et al.，2002；Moody，2004；Newman，2004b），也是右偏的。但是，对具有少量协作者的作者来说，它也有一个所谓的陷阱特征，这一特征被Wagner和Leydesdorff（2005）识别并被进一步Milojevi（2010）研究。这一特征很重要，科学研究团队形成和进化的模型（Milojevi，2014）已经揭示了其存在的潜在原因。它服从知识产生的两种模式：一个较小的核心团队服从泊松分布，另一个拓展的团队由于偏好链接能变得非常大。前者的分布在小值上有一个峰值，在陷阱中被反映出来。这些过程影响着网络拓扑结构。

网络的一种重要特性是连通性。如果网络是不连通的，那么一些节点对就不能到达彼此。基本方式之一是通过连通分量识别这些关系紧密的子群的存在。特大连通分量的规模可以表示为其中所有节点的比例。理解了连通分量的分布，尤其是特大连通分量的出现，在协作研究中可用于研究一个学科的出现。也就是说，网络中一个健壮的特大连通分量的存在已经被解释为领域形成的一个标志。大型连通分量规模的增加预示着从一个相对无组织的研究团体转变为一个科学领域。

为了识别Pajek中的连通分量，可点击Network＞Create partition＞Components＞Strong（见图3.12）。如3.3节所讨论的，对于一个有向网络，在强连通和弱连通分量之间有差别。如何选择依赖于我们想要解决的问题。

在《科学计量学》协作网络中有586个连通分量。最大的连通分量包含647个作者，如，所有作者中的28.2%在数据集中（见图3.13）。之后的三个大型分量规模较小，各自有28、20和20个作者。在Sci2中点击Visualization＞Networks＞Gusess可视化网络，然后在Layout选择GEM。关于网络可视化的更多信息可参见第13章。

在最大连通分量中作者间的平均距离是6.4，直径是17。在Pajek中计算距离可点击Nework＞Create Vector＞Distribution of Distances。上述结果显示，在《科学计量学》发表文章的研究者不是一个已建立的科学领域的部分。然而，想要获得更多领域形成的信息，我们需要评估纵向数据，不仅仅是某一时刻的快照。

(www.daowen.com)

图3.12　Pajek中识别连通分量

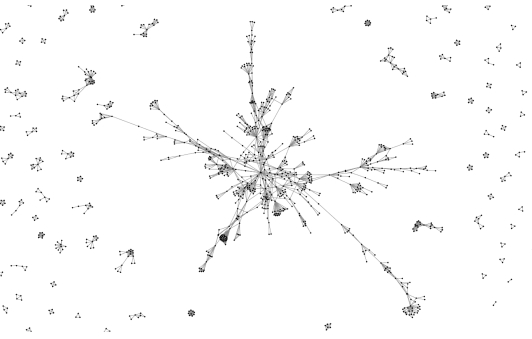
图3.13　协作网络中的最大连通分量

在得到这些基本的网络属性后，让我们把注意力转向有潜在用途的网络度量的一些指标。最流行的一个网络度量指标是中心性（或者是有向网络中的声望）。中心性的度量试图回答网络中谁最重要或谁是中心节点的问题。关于中心性，Freeman（1979）提供了一种综合分析方法。

主要的网络中心性度量可分为本地：度中心性度量和与网络其余部分相关的（如：基于网络中节点的位置），紧密度中心性、介数中心性和特征向量中心性（或者Bonacich能力）度量。这些度量最初都是为无权网络设置的。然而对加权网络的中心性度量也已经被研究了（Barrat et al.，2004；Newman，2004a；Opsahl et al.，2010），那些度量方法的应用和解释不是那么明确，因此不在本章作深入介绍。许多中心性和声望度量指标已经用于科学计量学。例如，在度量期刊的跨学科特性方面，Leydesdorff研究了介数中心性的使用（Leydesdorff，2007；Leydesdorff，Rafols，2011）。他发现归一化的介数中心性是跨学科特性的一个好指标。他研究了《科学引文索引》（Science Citation Index）和《社会科学引文索引》（Social Science Citation Index）2004年收录的7379种期刊的中心性度量^[2]。关于期刊指标的另一项研究是Leydesdorff（2009）将传统的期刊指标（如影响因子）和中心性度量及PageRank进行了对比，发现PageRank（我们会在后文中讨论）不是一个影响力指标。最后，Abbasi、Hossain、Leydesdorff（2012）研究了协作网络的进化，发现那些高介数中心性的作者比那些高度中心性和紧密度中心性的作者更能吸引合作者。

要在Pajek中计算度、特征向量、介数和紧密度中心性等，可点击Nework＞Create Vector＞Centrality并分别选择Degree＞All，Hubs-Authorities，Betweenness和Closeness＞All（见图3.14）。在有向网络中，Hubs-Authorities计算Hubs和Authorities，但在无向网络中，Hubs和Authorities是相同的，而且和特征向量中心性度量一样。

在Pajek的Vectors区域，点击Report窗口中的i按钮可看到结果。在同一区域点击Magnifying Glass按钮（“View/Edit Vector”），我们能看到所有的名字和隶属于名字的值。

图3.14　Pajek中计算度中心性、特征向量中心性、介数中心性和紧密度中心性

最简单的本地中心性度量方法之一是度中心性。这个方法与社会资本的思想有关联。根据中心性度量，最突出的节点是那些在网络中与其他节点链接最多的。这些节点能使用链接影响其他节点，或者能更快地得到信息。根据度中心性，在《科学计量学》网络中最核心的五位作者是W.Glänzel、R.Rousseau、F.DeMoya-Anegon、B.Klingsporn、Ys Ho（见表3.1）。其中一个非常有趣的作者是B.Klingsporn，他证实了对较大型合作者团队的存在进行度量的敏感性。也就是说，他在10年的时间里仅在《科学计量学》上发表了两篇文章，其中一篇有21个合作者，是在整个数据集中合作者数量排在第二的。在此领域，那些强合作关系列表正变成一种创建协作者网络的标准选择方式，度量指标诸如中心性度量需要被仔细测试。

然而，并非所有节点在影响力或权力上是相等的。Bonacich（1987）是第一个提出考虑节点的不平等而拓展简单度中心性度量。也就是说，他提出一种度量方式，建立在一个想法的基础上，即在和其他重要的节点建立连接后，网络中一个节点的重要程度可能增加。这种度量方式就是特征向量中心性度量，通过赋给每个节点一个与其邻居分值总和相对应的分值进行计算。因此，特征向量中心性的值可能会大，要么因为一个节点有很多邻居，要么因为它有重要的邻居（或者两者都是）。这种度量方式很适用于无向网络。根据特征向量中心性，在《科学计量学》网络中最核心的五位作者是：W.Glänzel，B.Thijs，A.Schubert，K.Debackere，B.Schlemmer（见表3.1）。和度中心性度量比较，我们看到最核心的作者列表已经发生显著变化（除了Glänzel，两种方式都是最高的）。除了Glänzel和Debackere（他的度中心性是23，在列表中排第六），其他基于特征向量中心性的核心作者都有相对较低的度中心性。最明显的优点是有较少链接，但非常有影响的个体能被看到，在Schlemmer例子中，他的度中心性为3（根据度中心性，他在最核心作者列表中排在670位）。他的位置通过与协作网络中最核心的作者Glänzel合写五篇文章得以确保。有趣的是，Thijs（在特征向量中心性中第二个重要作者）发表的22篇中有21篇是和Glänzel合作的。

表3.1　基于《科学计量学》数据集，利用四种中心性度量方式计算的14位作者的值和排名（小括号内）

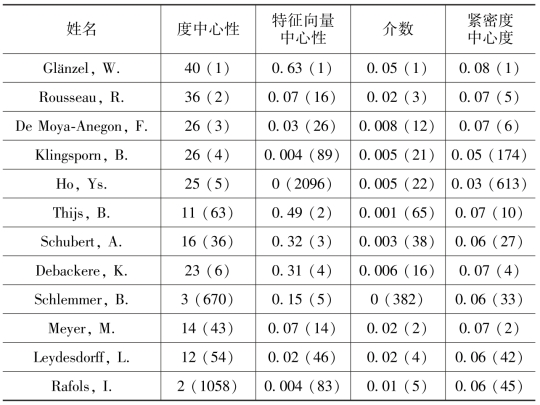
在权力、地位和影响力研究方面，度中心性和它的演变已被证明是有用的。然而，这些中心性度量不可能在所有环境下都是最好的。例如，度中心性在描述团体间的代理人方面是不充分的，或者可能是网络中任何来源的信息都将到达一个特殊的节点。对这些情况，更好的中心性度量是介数中心性。高介数中心性的节点可能不仅作为不相连社区间的通信使者，而且可能作为看门人，因为它们拥有控制信息通过其他节点的权力。根据介数中心性，在《科学计量学》网络中最核心的五位作者是：W.Glänzel，M.Meyer，R.Rousseau，L.Leydesdorff，I.Rafols（见表3.1）。这组中最有趣的作者是I.Rafols，在数据集中他只发表了3篇文章，只有2位合作者（M.Meyer和A.Porter）。尽管如此，他是连接57位研究者和围绕Glänzel图中最核心部分唯一的链接。看图示非常明显，最核心的作者实际上是作为桥梁的（见图3.15）。

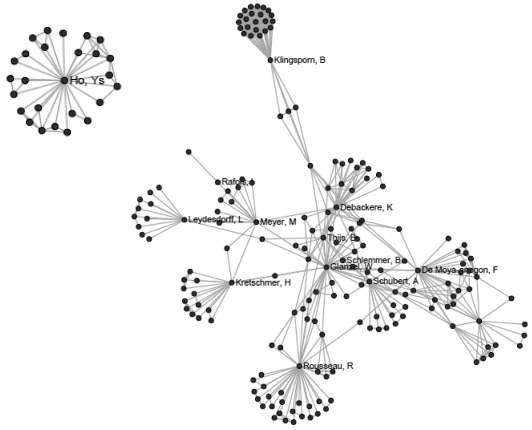
图3.15　基于至少一种中心性度量方式，《科学计量学》数据集中14位作者的协作网络和他们的协作者

最后，也有这样的环境，和多数节点的直接联系不是很重要，不同社区间的代理也不重要，但需要看离中心距离的远近。这种用于识别网络中的个体能多快地到达其他节点的度量方式叫作紧密度中心性度量。紧密度中心性是建立在一个节点和网络中其他节点的平均最短路径长度的基础上。有高紧密度中心性的节点，例如，那些在网络中比较靠近其他节点的节点能够有机会让它们的观点在社区中更快地被听到。根据紧密度中心性，在《科学计量学》网络中最核心的五位作者是：W.Glänzel、M.Meyer、H.Kretschmer、K.Debackere和R.Rousseau。

总之，协作网络已经用于更好地理解科学的社会结构，尤其是科学团体间的联系（和联系的潜力）。因此，我们所讨论的不同的中心性度量方式有能力识别在通过社团传送信息、共享观点、促进跨学科和跨领域方面是由哪个个体扮演或者有潜力扮演重要的角色。在21世纪初，我们已经识别出《科学计量学》期刊研究团体最核心的两个作者是W.Glänzel和R.Rousseau。根据中心性的四种度量方式，Glänzel已经被识别为最核心的研究人员（数据集中最高产的作者）。这位研究人员的核心作用已经被《科学计量学》期刊的新编辑所证实。另一个最核心的作者R.Rousseau是除了特征向量中心性度量外所有度量方式中排在前五的作者（数据集中第二高产的作者）。与其他最活跃的作者比，他在特征向量中心性度量中的排名较低（第16位核心作者），可能是由于较少重复合作及与大量较少协作的个体合作的综合结果。这个作者的重要作用也已经被外界所证实，他自2007年起已经是国际科学计量学和信息计量学协会（International Society for Scientometrics and Informetrics）的主席。