Map Equation的理论基础是基于流和信息论的，最早被Rosvall和Bergstrom（2008）引入。值得一提的是Map Equation利用了二元性，即在网络中查找社区结构和最小化随机游走运动的描述长度间的二元性。也就是说，给定一个网络的模块分区，就有描述随机游走运动的相关信息，或者可能存在的经验流。一些分区给出的描述长度短，另一些分区给出的描述长度长。就网络动力学而言，最短描述长度的分区恰恰是那个可最佳获取的网络结构。

如果网络中有些区域随机游走倾向于待一长段时间，Map Equation的底层代码结构就能被设计成压缩描述。因此，就网络动力学而言，一个作为真实流代理的随机游走，在所有可能的网络分区上最小化Map Equation来表明网络结构的重要方面。也就是说，Map Equation是一种直接的度量方法，可以度量给定的网络分区如何很好地获取模块化规律。

Map Equation基于流的理论基础很适合文献计量分析，因为在分析研究人员如何通过阅读文献和相应的引文进行学术导航时，引文网络的随机游走是一种合适的模型。图1.2就是网络中随机游走移动的呈现图。例如，在引文网络中，或者在基于期刊级别的引文集合中，通过Map Equation识别出的模块对应着研究领域。与此类似，在合作者网络中，通过Map Equation识别出的模块对应着研究群体。

为了解释Map Equation的原理，我们首先导出其表示，然后通过例子说明，这些互动的演示例子可在www.mapequation.org/apps/MapDemo.html获得（见图1.2、图1.3、图1.4）。但是，我们首先对Map Equation的原理给出一个简要的介绍：网络中随机游走的数学机理和基本的信息理论。对Map Equation理论原理不感兴趣的读者可到1.3节、1.4节看说明的例子。

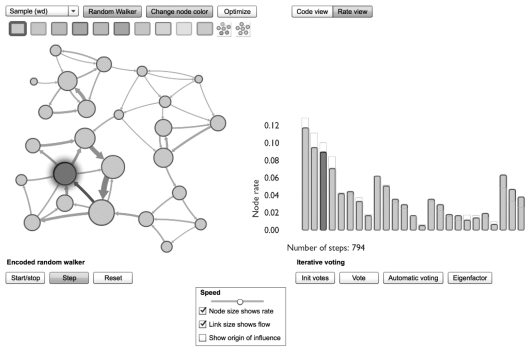
图1.2　在网络中随机游走的Map Equation演示图

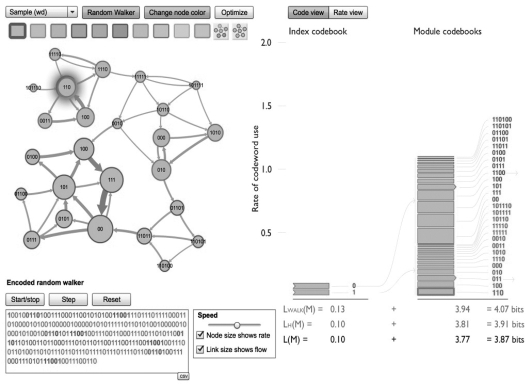
图1.3　在二模网络中随机游走的Map Equation编码演示图

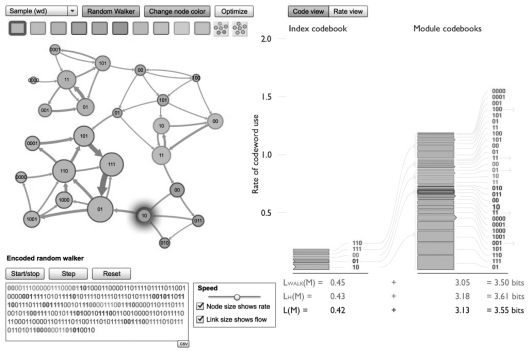
图1.4　在最优化五模块网络中随机游走的Map Equation编码演示图

（彩图可参考原著）

1.3.1.1　随机游走网络建模的动力学

Map Equation测量在网络中随机游走的模块所描述的每一步的理论下限。与测量一长步的代码长度和划分为一些步骤相比，这种方式更高效，它能从节点和链接的随机游走稳定分布中提取代码长度。总之，给定一个n个节点的网络，在节点α，β∈{1，2，…，n}间存在带权重的链接Wα→β，从节点α到节点β随机游走步骤的条件概率通过相对链接权重给出式（1.1）。

在Flash中的应用例子可在www.mapequation.org/apps/MapDemo.html获取。遵循与其权重相称的有向链接，随机游走从一个节点到另一个节点移动。在图1.2显示的快照中，随机游走用了794步，而且根据图右的频率分布遍历了节点。当前访问的节点在网络和柱状图中呈高亮显示。

假定pα给出稳定分布，理论上则可以从递归系统中推导出式（1.2）。

然而，为确保一种独特的解决方案独立于有向网络中随机游走开始的位置，因此，以低速τ随机漫步而不是传送一个随机节点。因为多数结果对传送参数τ的依赖较小，所以我们经常使用一个节点的与指向此节点的所有链的总权重比值（Lambiotte，Rosvall，2012）。稳定的分布由式（1.3）给出。

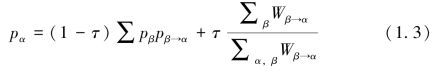
利用幂迭代方法（Golub，Van Loan，2012）能够有效地解决方程系统。

为确保结果对传送参数τ更具鲁棒性，我们使用非记录传送步骤仅记录链接的步数（Lambiotte，Rosvall，2012）。和式（1.3）类似，我们无需一个固定方案上的远程瞬移，而是使用附加步骤获得这些变化，加上一个到达此节点的与离开此节点的所有链的总权重比值。

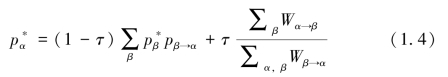
对未记录的链接访问频率qβ→α和节点pα可以表示成式（1.5）和式（1.6）。

这就是所谓的智能传送机制，确保方案独立于有向网络中随机游走开始的位置，而且对根据传送参数计算得到的结果影响最小。传送频率的标准值是τ＝0.15，但实际上聚类结果显示传送参数在一个范围内τ∈（0.05，0.95）仅有小的变动（Lambiotte，Rosvall，2012）。例如，对无向网络来说，结果完全独立于传送率，和式（1.2）计算出的结果一样。对于有向网络，传送率几乎接近于0，结果依赖于随机游走最初是怎么被激发的，这一点应该避免，但是传送值为1则意味着使用链接权重作为稳定分布。相应地，未记录的传送机制也使得描述通过链接自身给出的原始流成为可能，没有首先引入随机游走动力学。1.3.2节介绍的Infomap能够使用上述规律，但是，为得到更具鲁棒性的结果，我们建议使用与链接权重相称的未记录传送机制。

Map Equation是不受外部参数约束的。相反，方案的规模可以动态设置。上述的动态性对应于随机游走访问节点的每一步编码，但代码等级可设置成低和高（Schaub，Lambiotte，Barahona，2012）。较高的代码等级能通过指向内部的链接获得，较低的代码等级可通过增加非本地链接获得（Schaub et al.，2012）。因为随机游走会在更小的区域受限制，所以编码等级高的会导致更小的模块。Infomap代码允许通过随机游走每一步访问的节点编码的自然值来提高编码等级。

1.3.1.2　基本信息理论

当Map Equation给出网络中一个随机游走模块描述的理论最底限时，交互的Map Equation示例证明了用真实编码语言的描述。我们使用哈夫曼编码（Huffman，1952），这个是最优的，在某种意义上说，没有什么二进制编码比它更靠近理论值。然而，为了识别出网络中的最优分区，我们只对压缩率和非实际的码字感兴趣。相应地，Infomap算法只计算由Map Equation给出的理论极限。(www.daowen.com)

申农（Shannon，1948）的编码理论认为描述n个独立和等分的随机分布变量的理论最低值由概率分布的熵值给出。也就是说，给定概率分布P＝{pi}，∑ipi＝1，那么每步编码长度的最底限是：

用底数为2的对数以比特为单位测量编码长度。或者说，没有码书能够根据P给出的事件分布码字在平均水平上使用更少的比特位。

相应地，网络中随机游走动力学的最好压缩方式是由熵速率给出的（Shannon，1948）：

式（1.8）对应着由当前节点位置给出的下一个访问节点的平均代码长度，即在所有节点位置的平均值。这种编码机制利用由当前节点位置给出的下一个要访问节点的独立性和恒分布性，但是不能利用网络的模块结构。然而，Map Equation使用附加的限制条件，使得从一步到下一步的可靠信息只来源于当前访问的模块或者模块间的随机游走开关，独立性和恒分布性限于模块内和模块间。考虑网络动力学，这种假定自然遵循了模块化描述被表示网络模块结构的网络分区最大化压缩。

1.3.1.3　Map Equation的数学原理

给定一个网络分区，Map Equation定义了理论的模块描述长度，体现了我们能够多精确地描述随机游走的轨迹，这些轨迹受可能加权的有向网络链接引导。我们使用M表示具有n个节点m个模块的网络分区，每个节点α对应一个模块i。然后，我们寻求最小化描述长度L（M），是由可能的网络分区M的Map Equation给出的描述长度。再一次，考虑网络动力学，给出最短描述长度的网络分区能最佳地获取到网络的社区结构。

Map Equation能用申农的源编码定理以紧凑格式表达，如式（1.7），对多种码书的每一种，可以用它们的使用频率给它们赋权值。描述长度和使用频率能以节点—访问频率pα表示，模块转化频率qi←和qi→分别表示随机游走进入和退出模块i的频率：

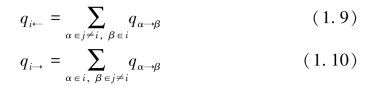
为了利用网络的模块结构，m模块编码书和一本索引编码书各自用来描述随机游走在模块内和模块间的运动。对每个节点α∈i，模块编码书i有一个码字和一个退出码字。码字的长度来自随机游走访问模块内节点的频率pα∈i和离开模块频率qi→。我们用pi←指代这些频率的总和，即在模块i中码字总的使用之和，Pi指代归一化概率分布。我们需要表达编码书索引中码字的平均长度和根据其使用频率赋予模块编码书的权重。因此，Map Equation为：

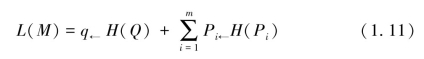
表1.2中我们详细解释了Map Equation的形式，在图1.3和图1.4中我们提供了霍夫曼编码的例子来进行说明。

表1.2　Map Equation形式

续表

1.3.1.4　Map Equation的原理

Map Equation的示例可在www.mapequation.org/apps/MapDemo.html获取，它提供了可交互的界面，可帮助我们理解Map Equation的原理。示例有两种模式，通过频率视图（Rate View）和编码视图（Code View）这两个按钮实现。图1.2中频率视图的目的是说明我们如何使用随机游走来引导网络中的流。图1.3和图1.4中编码视图的目的是说明在网络结构中找规律和通过网络结构引导的流描述压缩间的二元性。

在Flash应用（可在www.mapequation.org/apps/MapDemo.html获取）中，随机游走目前访问的绿色节点用码字110（见图1.3）。在码书索引中的块高度表示随机游走进入模块的速率。紧邻每个块的位序列是相关的码字。类似地，在模块码书中的块高度表示随机游走访问一个节点或退出一个模块的速率。表示退出速率的块在其右边有个箭头。左下角的文本区域显示了随机游走的前一步编码，是以到码字110的节点为结束。两个模块的步子分别以绿色和蓝色高亮度显示，进入和退出的码字是粗体。右下角的L（M）表示由式（1.11）给出所选择的两个模块网络分区的描述长度的理论限值。LM（M）表示由实际码书给出的哈夫曼编码的限值。LWALK（M）表示在仿真模拟中实际行走的每一步描述长度的平均值。

从速率的角度看，点击Random Walker和Start/Stop，一个随机游走开始穿越网络。从一个节点到另一个节点，由式（1.1），随机游走选择下一个节点的根据是和其邻居节点间链接的权重相称的节点。正如1.3.1.1节所描述的，为确保一个遍历解，平均访问速率将会达到一个相对稳定的状态，不依赖随机游走开始的位置。随机游走有时不管链接结构，会移动到一个随机节点。在此试验中，随机游走每步有15%的概率传送到一个随机节点或者每六步可能到一个随机节点。

在速率视图中，右边的柱状图显示访问节点的分布。色条显示了到目前为止的平均分布，灰色边框显示了遍历解。遍历解的访问速率对应于由网络决定的转移矩阵最大特征值的特征向量。这一解也对应于节点的PageRank值（Brin，Page，1998）。一长段时间过后，随机游走的平均访问速率将会接近遍历解，但是这种基于走步的方法非常没有效率。实践中，因为Map Equation仅使用遍历速率作为输入，因此我们使用幂率迭代方法求遍历解（Golub，Van Loan，2012）。幂率迭代方法使用随机游走的概率分布而不是具体的随机游走。通过选择Init Votes，每个节点接收到概率的一个平均份额。通过点击Vote，每个节点的概率被推送到与其链接权重对应的邻居节点，其中15%是自由分布的。正如点击Vote一段时间所看到的，概率分布快速地接近遍历解。

图1.3中，与两模块方案相比较，索引码书比我们通常使用的要大。尽管如此，归功于较小模块码书中模块内更高效的运动编码，每一步码长比平均值短0.32位。

在编码视图中，每个节点都用其码字作了标记（见图1.3、图1.4）。每个事件也被表示为右边堆栈中的一块，比如随机游走访问一个节点、进入一个模块或退出一个模块。索引码书中的堆栈显示了进入模块事件，模块码书中的堆栈显示了模块内的事件。在Map Equation演示中，鼠标移动到一个节点或者一个块都会高亮度显示。块高度表示相应事件发生的速率，每个块右边的位串是与事件关联的码字。码字是哈夫曼编码（Huffman，1952），取自它们的使用频率。给定一个概率分布，对使用二进制码字进行逐字符编码来说，哈夫曼编码是最理想的。如1.3.1.2节解释的，哈夫曼编码的平均码长是有下限的，即概率分布的熵（Shannon，1948）。总之，哈夫曼编码的平均码长比由熵给出的理论限值要稍微长些，在使用整数长度的码字上没有限制。例如，在图1.3和图1.4的右下角，实际二进制码字的平均长度比理论限值要长约1%。

在实践中，为了利用查找社区结构和最小化描述长度的二元性，我们使用Map Equation给出的理论限值。也就是说，在Map Equation示例中，我们显示的码字仅用于教学。例如，为那些经常被访问的节点指派短码字，为那些不被经常访问的节点指派长码字，所以描述长度要比平均值短。类似地，随机游走经常访问的模块被指派短码字，依此类推。这种变化的码字长度利用了一些事件要比其余经常发生的事件更规律，但没有利用网络的社区结构。然而，索引码书和模块码书的模块编码结构却运用了社区结构。

最优化的网络分区对应一个模块编码结构，均衡了在模块内和模块间指定运动所付出的代价。图1.3显示了具有两个模块的网络分区。模块内指定运动的平均描述长度的底限是每步3.77位，进入模块的指定运动每步只有0.10位。进入模块的运动描述代价低，因为一旦在模块间转换，一个独立位是必需的，用来说明随机游走进入了两个模块中的哪一个，而且平均每十步转换一次。但是，模块内的运动代价相对要高些，因为每个模块内部含有很多节点，每个节点有一个相对较长的码字。一本码书包含的事件越多，码字的平均长度越长。图1.4显示了具有5个模块的最优化网络分区。在这个分区中，较小的模块允许在模块内对运动更有效率的编码。平均而言，在模块内指定运动需要每步3.13位，在图1.3中的两模块分区要少0.64位。这种压缩获益可导致对5个模块间的运动描述花费更高的代价，但不管怎样，总的码长会更短些，相比2个模块分区的3.87位，在最优化方案中只有3.55位。为了更好地理解Map Equation的内部机理，可以在Map Equation示例中通过改变网络的分区，研究编码结构和相关联的编码长度是如何变化的。

这里我们已经介绍了基本的两层Map Equation。Map Equation Framework的一个重点是，总是能达到高阶结构，例如达到层级结构（Rosvall，Bergstrom，2011）、交叠结构（Esquivel，Rosvall，2011），或者更高阶的马尔科夫动态（Rosvall et al.，2013）。关于这些方法更详细的内容，请阅读本书参考文献。