1.特性仿真激励信号

设特性仿真谐波激励x=Asin（2πft），A为激励位移幅值，f为激励频率，最大仿真速度为V_max。

（1）仿真激励频率f根据仿真所需要的最大速度V_max=ωA=2πfA，可以求得在确定幅值下激励信号频率为

（2）仿真激励周期T根据频率f和周期T之间的关系，可以求得仿真激励信号周期为

因此，将激励信号频率f代入上式，可得仿真激励信号的周期为

（3）仿真激励位移x对激励位移x=Asin（2πft），在各个时间点上速度的数值可以表示为

x（i）=Asin（2πfΔt·i） （11-54）

式中，Δt为离散数据时间间隔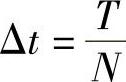，，N为仿真激励信号周期的离散点个数；i为任意第i个离散点。

（4）仿真激励速度V对激励位移求导，可以得到相应位置的仿真激励速度，即

V=2πfAcos（2πft）

因此，在各个时间点上速度的数值可以表示为

V（i）=2πfAcos（2πfΔt·i） （11-55）(www.daowen.com)

（5）仿真激励加速度a对位移求二次导数，可以得到相应位置的加速度，即

a=-4π²f²Asin（2πft）

因此，在各个时间点上加速度的数值可以表示为

a（i）=-4π²f²Asin（2πfΔt·i） （11-56）

2.活塞杆惯性力F_a

由活塞及活塞杆的质量和仿真激励加速度a，可得活塞杆惯性力F_a，即

F_a=m·a=-4mπ²f²Asin（2πft）

式中，m为活塞及活塞杆的质量。

在活塞杆惯性力各个时间点上的数值可表示为

F_a（i）=-4mπ²f²Asin（2πfΔt·i） （11-57）