如图11-6所示，由于蓄能器出口与油液管路相连，则在出口处存在局部压力损失p₃₄可表示为

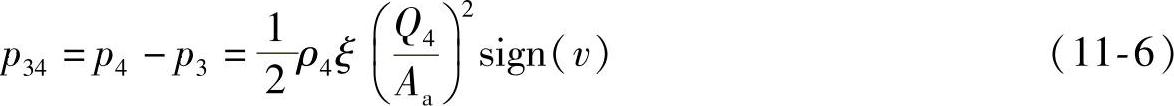
式中，ρ₄为蓄能器出口处油液的密度；ξ为局部压力损失系数；Q₄为蓄能器出口流量；A_a为蓄能器出口截面积；sign（v）表示油气弹簧运动速度方向的符号函数。

蓄能器内的气体为氮气，其气体性质与理想气体相近，可用气体状态方程来描述，即

式中，n为气体多变指数（1.0～1.4）；p_q0和V_q0分别为储能器的初始充气压力和体积；p_q和V_q分别为储能器的瞬时气体压力和体积。

当蓄能器内的气体被看做理想气体时，上述气体状态方程可简单表示为

p_q0V_q0=p_qV_q

忽略蓄能器中油液与气体间作用力的延迟，即p₄=p_q，则蓄能器中气体体积变化量可以表示为

ΔV_q=V_q-V_q0=∫Q₅dt （11-8）

式中，Q₅为蓄能器中油液的体积流量。(www.daowen.com)

根据式（11-3）和式（11-4），蓄能器中油液的体积流量可表示为

将式（11-9）代入式（11-8），可得蓄能器中气体体积变化量为

设储能器的截面积为S_q，则浮动活塞位置高度的变化量Δx_g为

因此，如果将油气弹簧储能器中的气体看做是理想气体，则油气弹簧储能器的刚度可表示为

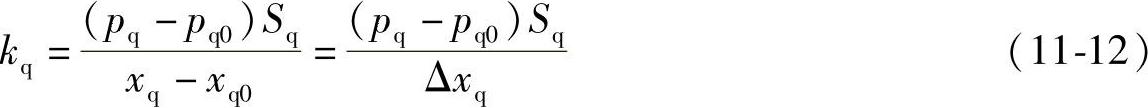
式中，x_q0为油气弹簧储能器浮动活塞的初始位置高度；x_q为储能器浮动活塞位置；Δx_q为储能器浮动活塞偏离初始位置的高度差。