基于车辆参数的减振器阀系参数设计，其关键点是如何根据车辆参数（车辆类型、簧上质量、车身固有频率、最佳阻尼比、平安比和杠杆比）确定出与车辆悬架达到最佳阻尼匹配的减振器速度特性曲线，然后根据所得到的减振器最佳阻尼匹配速度特性曲线，利用基于速度特性减振器阀系参数的优化设计方法，对减振器阀系参数进行优化设计。

设单轮总质量为m_t，单轮簧下质量为m_d，则单轮簧上质量m_u=m_t-m_d。按1/4单自由度振动模型，根据悬架系统最佳阻尼比，可得悬架系统最佳阻尼系数为

c_s=4πξf₀m_u （8-54）

式中，ξ为悬架最佳阻尼比，是由被动悬架的最佳阻尼匹配所决定的；f₀为悬架固有频率。

因此，根据悬架系统杠杆比i，可求得减振器复原行程在首次开阀时的阻尼系数为

根据减振器平安比η_ps的定义，可得

η_ps=k₁/k₂=c_d1/k₂ （8-56）

式中，k₁为减振器首次开阀前的速度特性直线斜率；k₂为最大开阀前的速度特性直线斜率。

因此，可得减振器复原行程最大开阀前速度特性曲线的斜率k₂为

k₂=c₁/η_ps （8-57）

根据阻尼力与阻尼系数和速度之间的关系，可得到减振器复原行程最大开阀阻尼系数c_d2为(www.daowen.com)

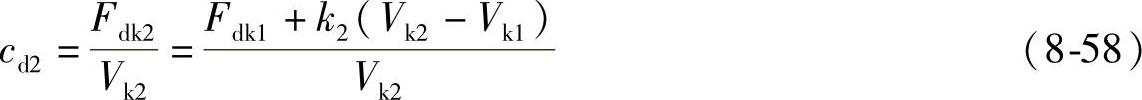
式中，V_k1和V_k2分别为减振器首次开阀速度和最大开阀速度；F_dk1和F_dk2分别为减振器在首次和最大开阀时的阻尼力。

将F_dk1=c_d1V_k1和k₂=c_d1/η_ps代入式（8-58），得

根据减振器压缩行程和复原行程阻尼特性的双向比β_d，可得减振器压缩行程在开阀前、后的阻尼系数分别为

由以上分析可知，利用车辆参数以及复原行程和压缩行程的初次开阀速度和最大开阀速度，可求得减振器复原行程的首次开阀阻尼力F_dk1和最大开阀阻尼力F_dk2，以及压缩行程的首次开阀阻尼力F_dk1y和最大开阀阻尼力F_dk2y。因此，可得设计减振器要求的分段线性速度特性曲线，如图8-21所示。

图8-21 基于车辆参数的最佳阻尼匹配减振器速度特性曲线