1.阀片厚度优化设计目标函数

常通节流孔设计确定后，根据开阀后的不同速度点，所设计得到的节流阀片厚度不同，则减振器开阀前的速度特性不同，如图8-18所示。

对复原阀片h_f可建立优化设计目标函数，进行曲线拟合优化设计。设阀片设计厚度h_fj减振器速度特性曲线在速度范围[V_k1，V_k2]所组成的面积，即代表设计阀片厚度减振器在该速度范围内的功率P_Dj；而目标要求速度特性曲线在速度范围[V_k1，V_k2]所组成的面积，代表减振器在速度范围[V_k1，V_k2]内设计要求功率P_dj，则复原阀片厚度h_f的曲线拟合优化设计目标函数为

目标函数随速度的变化曲线如图8-19所示。

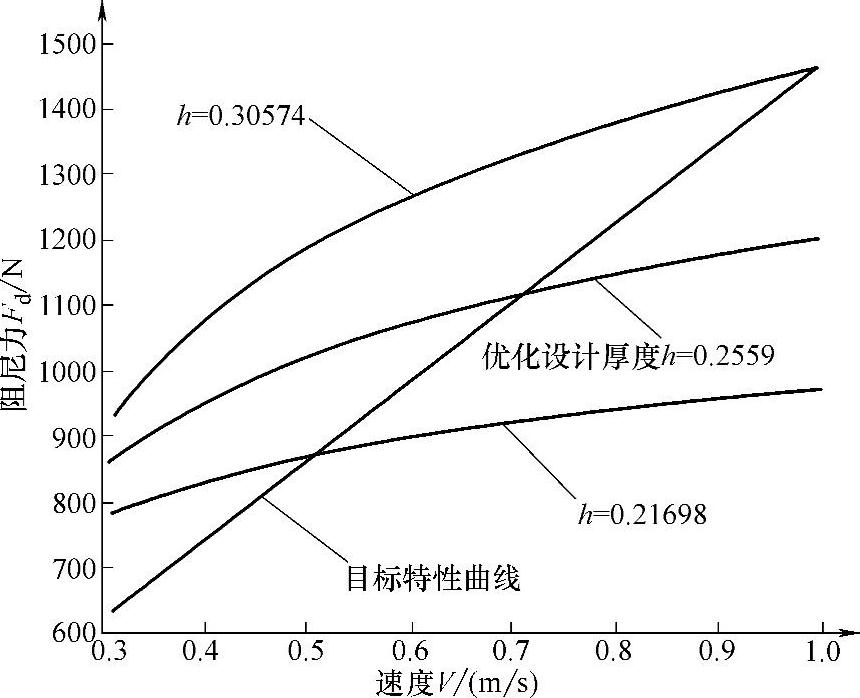
图8-18 不同阀片厚度下的复原速度特性曲

由此可知，目标函数存在极值点，极值点不仅与速度离散点的个数有关，还与减振器结构参数有关。例如，在常通节流孔面积A_0f不同的情况下，优化设计速度点也不同。因此，必须是在常通节流孔面积设计确定之后，才能对阀片厚度进行优化设计。

2.最优阀片厚度h_f

当目标函数P_D-dhj达到最小值时，所对应设计速度点即为最优阀片设计厚度速度点，所对应阀片厚度即为节流阀片优化设计厚度，如图8-20所示。

图8-19 目标函数随设计速度变化曲线

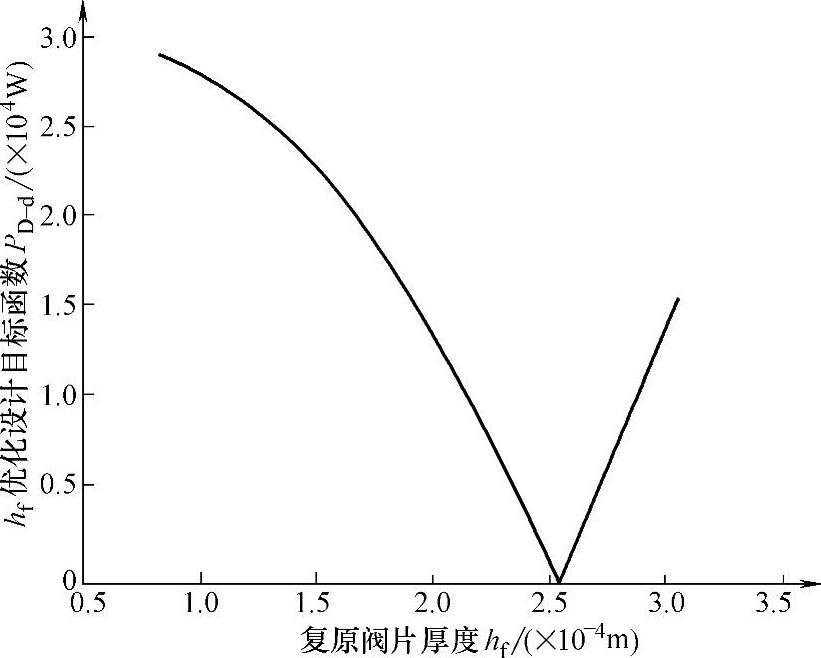
图8-20 目标函数随阀片厚度h_f的变化曲线(www.daowen.com)

3.优化设计过程

1）利用速度点V_j∈[V_k1，V_k2]，j∈[1，2，…，n]，设计节流阀片厚度h_j。

2）对设计阀片h_j计算在速度[V_k1，V_k2]范围内各速度点的阻尼力值F_Dj。

3）建立阀片厚度优化设计目标函数P_D-dhj=P_Dj-P_dj。

4）求阀片优化设计目标函数P_D-dhj的极值，极值所对应的速度点即为最优速度设计点，对应的阀片厚度h_i即为所求的最优阀片厚度。

4.基于速度特性的减振器其他阀系参数的曲线拟合优化设计

利用曲线拟合优化设计方法得到减振器常通节流孔面积A₀和节流阀片厚度h设计值之后，可根据初次开阀速度点和最大开阀速度点所要求的阻尼力，分别对减振器复原阀和压缩阀的阀片预变形量和最大限位间隙进行设计，即

1）复原阀片预变形量：

2）复原阀片最大限位间隙：

3）压缩阀片预变形量：

4）压缩阀片最大限位间隙：

因此，将曲线拟合优化设计得到的复原节流阀片厚度h_f和压缩节流阀片厚度h_y设计值，分别代入以上四式，便可以分别得到减振器复原阀的节流阀片预变形量f_rk0和最大限位间隙δ_maxf，以及压缩阀的节流阀片预变形量和最大限位间隙设计值。