1.弹性力学基本方程

根据弹性力学理论，橡胶衬套的应变与位移分量的6个几何方程分别为

橡胶衬套应变与应力分量的6个物理方程分别为

式中，E为弹性模量；G为剪切模量；μ为泊松比，对于橡胶材料，。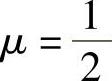

弹性模量、剪切模量和泊松比三者之间满足如下关系

把式（7-2a）～（7-2c）左、右两边分别相加，并把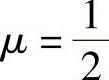代入，可得

ε_r+ε_θ+ε_z=0 （7-4）

由式（7-2a）～（7-2c）及式（7-4），可得

σ_r=σ_z+2G（2ε_r+ε_θ） （7-5a）

σ_θ=σ_z+2G（2ε_θ+ε_r） （7-5b）

在橡胶衬套中取微元六面体，并将各力投影到z轴上，得六面体的力平衡方程为

2.第一施加载荷情况下的变形

设橡胶衬套的内筒不动，在外筒施加向上的集中载荷F，同时在衬套两自由端施加应力载荷σ_z=δsin（θ-θ₁）；设外筒的位移为Δr₁，则橡胶衬套内P点的位移可表示为

u=U_rsin（θ-θ₁） （7-7a）

v=V_rcos（θ-θ₁） （7-7b）

w=0（7-7c）

式中，U_r和V_r仅为半径r的函数。

把式（7-7a）～（7-7c）代入（7-1a）～（7-1c），可得

ε_z=0 （7-8c）

把式（7-8a）～（7-8c）代入式（7-4），可得

根据式（7-2d）～（7-2f）、式（7-5）、式（7-8）和式（7-9），可得

τ_zr=τ_zθ=0 （7-10a）

把式（7-10a）代入式（7-6），可得

式（7-11）表明，在z方向上的应力分量σ_z是定值，而z=±L/2时，σ_z=δsin（θ-θ₁），故橡胶衬套内任何处都有

σ_z=δsin（θ-θ₁） （7-12）

把式（7-12）分别代入式（7-10c）和式（7-10d），可得

取半径r处的微元面，其边长为rdθ和dz，则载荷F可表示为

将式（7-10b）和式（7-13a）代入式（7-14），可得

在集中力F的作用下，z方向的正应力为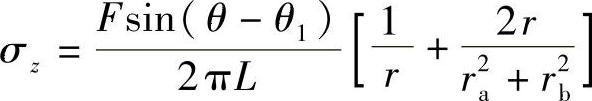，又σ_z=δsin（θ-θ₁），则

把式（7-16）代入式（7-15），可得

则式（7-17）的通解为

由式（7-9）和式（7-18）可得

根据边界条件U_r（r_a）=V_r（r_a）=0，由式（7-18）和式（7-19）得

由式（7-20）和式（7-21）可求得待定常数C₁和C₂分别为

把常数C₁和C₂分别代入式（7-18）和式（7-19），可得(www.daowen.com)

此时，橡胶衬套在径向（y方向）的变形量可表示为

即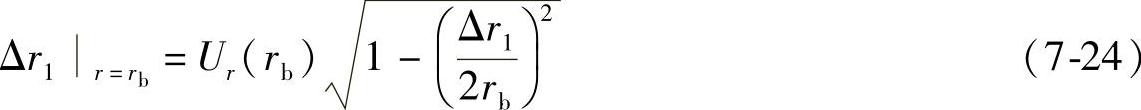

因此，可得在第一施加载荷情况下，橡胶衬套在径向y方向的变形量为

3.第二施加载荷情况下的变形

设橡胶衬套的内套筒不动，在橡胶衬套的两自由端施加反向应力载荷σ_z=-δsin（θ_-θ₁），此时外套筒的位移为Δr₂，则橡胶衬套内P点的位移表示为

u=Ysin（θ-θ₁） （7-26a）

v=Ycos（θ-θ₁） （7-26b）

w=w（r，θ，z） （7-26c）

把式（7-26a）～式（7-26c）代入式（7-1a）～（7-1c），可得

ε_θ=0 （7-27b）

把式（7-27）代入式（7-4），可得

根据对称性，在z=0处的横截面上，对于任意r、θ，都有w=0，因此，由式（7-28）积分可得

将式（7-26a）、式（7-26b）及式（7-29），代入式（7-1d）～（7-1f），可得

将式（7-30a）～式（7-30c）分别代入式（7-2d）～式（7-2f），可得

将式（7-27a）和式（7-27b）代入式（7-5a）和式（7-5b），可得

将式（7-31a）和式（7-31b）代入平衡方程式（7-6），可得

将式（7-33）对z积分，可得

将σ_zz=±L/2=-δsin（θ-θ₁）代入式（7-34），可求得常数C为

把式（7-35）代入式（7-34），可得

将式（7-36）代入式（7-32a）和式（7-32b），可得

由于在y轴方向没有施加载荷，故式（7-14）的右边等于0，将式（7-37a）和式（7-31c）代入式（7-14）可得

对式（7-38）积分可得

其通解为

式中，A₁、A₂、A₃为常系数；I（0，αr）、K（0，αr）为Bessel修正函数，且α=215/L。

下面根据边界条件，求常系数A₁、A₂和A₃。因为橡胶衬套镶嵌在内、外金属套筒之间，故w（r_a，θ，z）=w（r_b，θ，z）=0，即

根据边界条件，由式（7-41）可得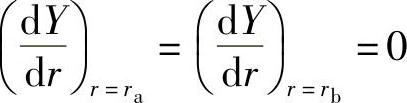，即

因为内套筒固定，所以Y（r_a）=0，由式（7-40）可得

由式（7-42）～式（7-44），可解得常数A₁、A₂和A₃。

因此，外套筒的变形可表示为

即

把式（7-25）代入式（7-45），可得在第二施加载荷情况下，橡胶衬套在径向y方向的变形量

4.径向变形叠加

根据变形叠加原理，两种施加载荷的变形叠加为在径向集中力F的作用下，橡胶衬套的y轴方向的变形量，即Δr=Δr₁+Δr₂。

把将式（7-25）和式（7-46）代入上式，可得橡胶衬套在集中力F作用下的变形量为