1.橡胶衬套的力学模型

圆环形橡胶衬套的轴向长度为L，其内、外圆的半径分别为r_a和r_b，并分别与刚性圆柱形金属内、外套管联结。内套管在固定位置夹紧，外套筒上施加径向力集中力F，使外套筒产生径向位移为Δr，如图7-1所示。

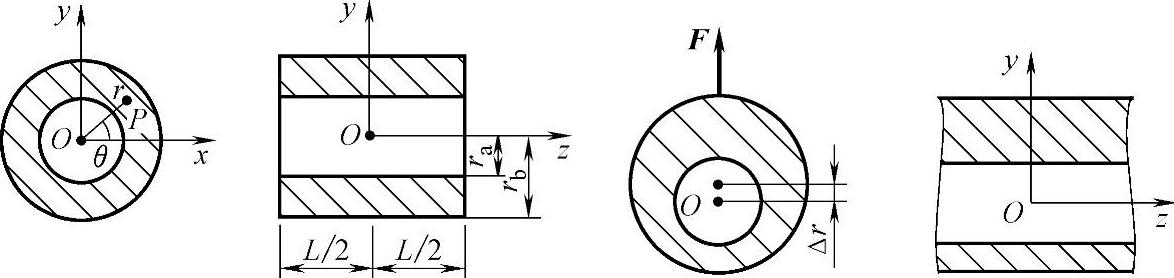
图7-1 橡胶衬套力学模型示意图

2.橡胶衬套的叠加力学模型

橡胶衬套的径向变形量可以利用变形叠加原理进行计算，在径向集中力的作用下，橡胶衬套的y轴方向的变形，可以分解为两种施加载荷情况下y轴方向变形的叠加，如图7-2所示。

第一施加载荷情况，如图7-2a所示，除了在外套筒上施加径向力F外，在橡胶衬套两自由端施加非均布应力载荷σ，以使两自由端保持为平面，此时，橡胶衬套径向的变形量为Δr₁。

在施加该载荷的情况下，所构建的非均布载荷应力函数σ=δsin（θ-θ₁），其中，δ仅为r的函数；θ₁为该载荷情况下的偏移角，即橡胶衬套径向变形为零处偏离x轴方向的角度，如图7-3所示，OO′=Δr₁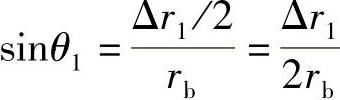，。其中，在θ∈（θ₁，π-θ₁）范围内，橡胶衬套为拉伸变形；在θ∈（-π-θ₁，θ₁）范围内，橡胶衬套为压缩变形。(www.daowen.com)

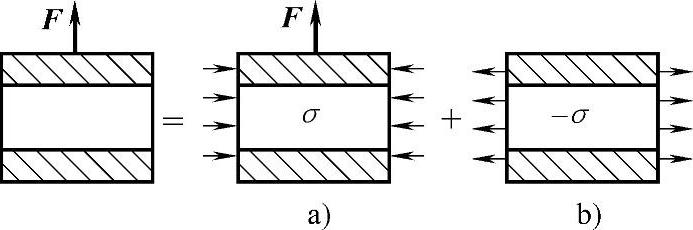
图7-2 橡胶衬套变形叠加示意图

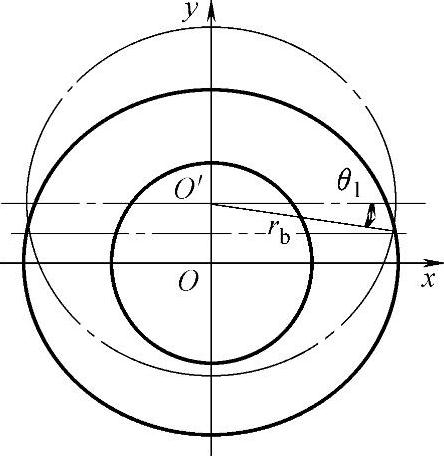
图7-3 橡胶衬套变形示意图

第二施加载荷情况，如图7-2b所示，为了抵消第一种施加载荷σ引起的径向变形，在橡胶衬套两自由度端施加非均布应力载荷-σ，故所构建的非均布载荷应力函数σ′=-σ=-δsin（θ-θ₁）。此时橡胶衬套径向的变形量为Δr₂，由橡胶衬套变形所引起的偏移角θ₂满足。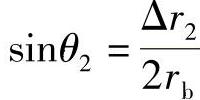

因此，根据叠加原理，在径向集中力F的作用下，橡胶衬套径向的总变形可表示为两种载荷情况下径向变形量之和，即Δr=Δr₁+Δr₂；总的变形偏移角θ₀满足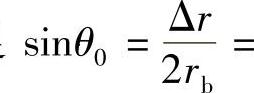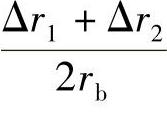，即sinθ₀=sinθ₁+sinθ₂。