1.多片不等长叠加钢板弹簧重叠部分的等效厚度

要解决多片钢板弹簧等效厚度的计算问题，首先要解决不等长的两片钢板弹簧的叠加问题。两片不等长叠加钢板弹簧的力学模型如图6-3所示，可以把图6-3中的力学模型等效为自由端受集中力F和弯矩M₀=F（L₁-L₂）的力学模型，如图6-4所示。要解决图6-4中所示力学模型的问题，必须解决图6-5所示的单片钢板弹簧的变形问题。

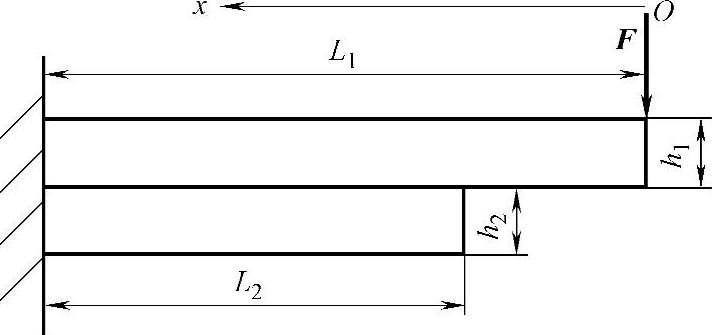
图6-3 两片不等长叠加钢板弹簧力学模型

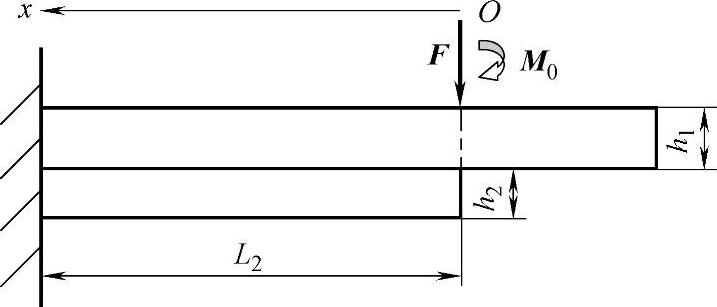
图6-4 两片不等长叠加钢板弹簧等效力学模型

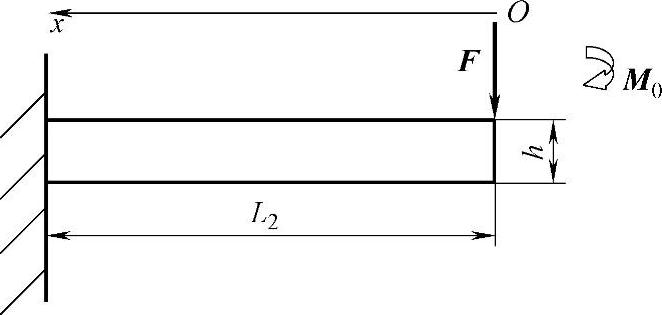
图6-5 单片钢板弹簧自由端受弯矩和集中力的力学模型

根据第2章2.2.2节的分析，可知钢板弹簧的变形微分方程为

式中，w为钢板瘫痪的挠度；I为钢板弹簧截面的惯性矩，且I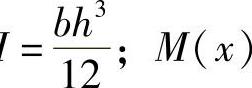为钢板弹簧任意截面x处的弯矩。

根据图6-5中钢板弹簧的力学模型，可得其任意截面上的弯矩为

M（x）=Fx+M₀=F（x+L₁-L₂） （6-21）

把式（6-21）代入钢板弹簧变形微分方程[式（6-20）]，可得

对式（6-22）积分，可得

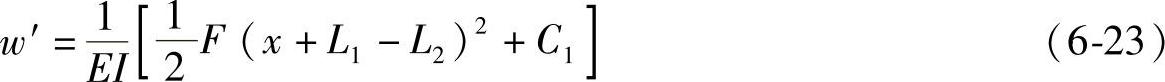
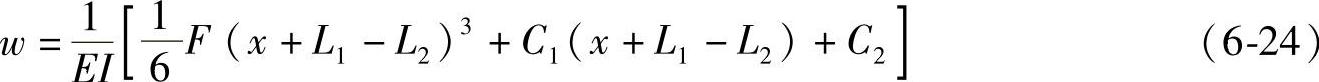
根据固定端的约束条件，可得变形w_A=0，转角w′_A=0，即

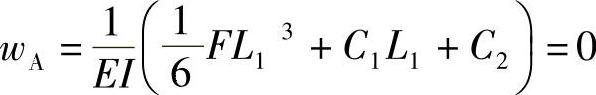
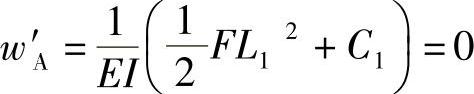
由以上两式可以解得常数C₁和C₂，即

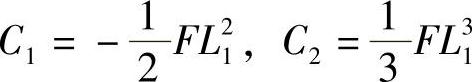
将常数C₁和C₂代入式（6-24），可得钢板弹簧任意位置处的挠度（变形）为

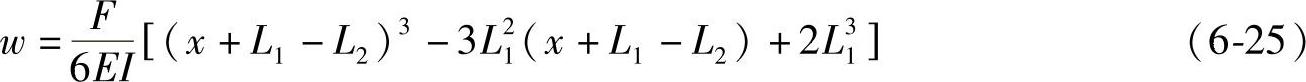
将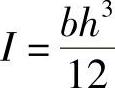代入式（6-25），可得

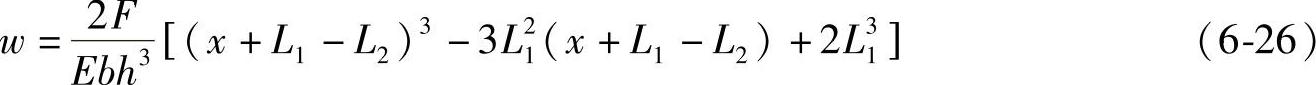
将式（6-26）提出因子F/h³，剩余因式归结为与厚度及载荷无关的变形“长城”系数G_x，即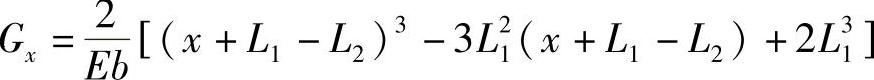，因此，式（6-7）可以表示为(www.daowen.com)

钢板弹簧任意截面上的抗弯截面系数为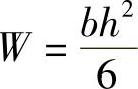，钢板弹簧任意截面上的正应力σ=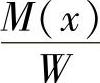，由此可得

由钢板弹簧的受力情况可知，n片不同厚度的钢板弹簧叠加在一起，且自由端受到集中力和弯矩时，各钢板弹簧所受的力不相等，但是各钢板弹簧承受的力之和等于总的载荷，即

F₁+F₂+…+F_n=F （6-29）

由钢板弹簧的变形情况可知，各钢板弹簧的弯曲变形量相等，且等于总的弯曲变形量。因此，由钢板弹簧变形解析式（6-27）可得

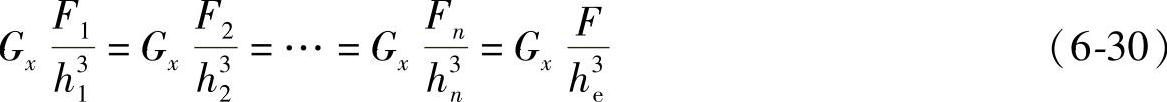
由式（6-29）和式（6-30），可得自由端受到集中力和弯矩的n片等长钢板弹簧的等效厚度为

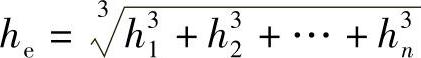
因此，n片不等长叠加钢板弹簧重叠部分（最厚部分）的等效厚度h_e为

由式（6-31）可知，图6-4中两片钢板弹簧的叠加厚度为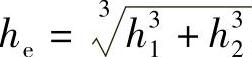，因此，图6-5中两片钢板弹簧重叠部分的等效厚度也为。

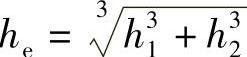2.多片不等长叠加钢板弹簧重叠部分的应力

通过上面的分析，可知多片不同（相同）厚度节流钢板弹簧叠加在一起，在集中力作用下，各叠加钢板弹簧重叠部分的弯曲变形量相等，都等于总变形量，即等于与重叠部分等长的厚度为h_e的单片钢板弹簧的变形量。

（1）叠加钢板弹簧重叠部分的受力 当n片钢板弹簧叠加时，根据式（6-29）和式（6-30），可得厚度为后h_i节流钢板弹簧所受力F_i，即

定义h_i/h_e=k_hi为叠加钢板弹簧重叠部分h_i的厚度系数，则式（6-32）可表示为

（2）叠加节流钢板弹簧重叠部分的应力 将式（6-33）代入钢板弹簧应力解析式（6-27），可得厚度为h_i的钢板弹簧的应力为

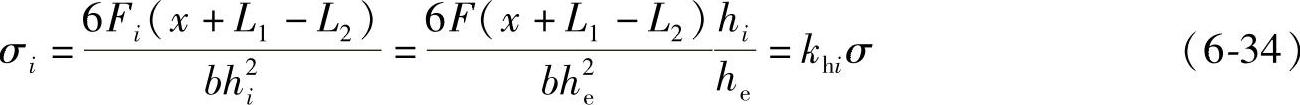
由式（6-34）可知，各叠加钢板弹簧重叠部分应力的大小，与叠加钢板弹簧重叠部分厚度的厚度系数k_hi成正比，也就是与钢板弹簧的厚度成正比。因此，n片厚度分别为h_i的叠加钢板弹簧，其重叠部分的最大应力σ_imax，也是钢板弹簧每片的最大应力σ_imax，即

σ_imax=k_hiσ_max （6-35）

定义第i片叠加钢板弹簧的应力系数为

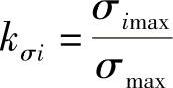
可知，第i片叠加钢板弹簧重叠部分的应力系数等于叠加钢板弹簧重叠部分的厚度系数，即

k_hi=k_σi （6-36）

由式（6-35）可知，叠加钢板弹簧的最大应力发生在重叠部分，而且是发生在最厚的一片钢板弹簧上。