减振器采用多片不同外半径的叠加阀片，可以使得叠加阀片各横向截面的应力近似，从而使阀片成为近似的等强度阀片，这样可以提高阀片材料的利用率，同时降低阀片应力，延长阀片的使用寿命。

多片不同外半径节流阀片叠加在一起，在轴对称力作用下，各叠加阀片在重叠部分的弯曲变形量相等，且都等于总变形量；各叠加阀片所受的力不相等，且在重叠部分各阀片所承受的压力之和等于总的压力。因此，其物理模型可以看做是长度不同、刚度不同（相同）的弹簧并联，如图5⁃22所示。

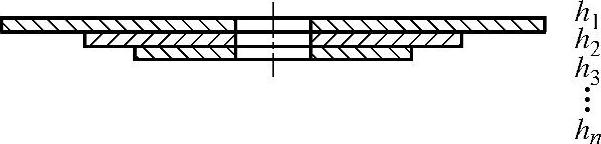
图5⁃22 不同外半径叠加阀片物理模型

不同外半径叠加阀片等效厚度计算及等效拆分的依据，都是不同外半径叠加阀片在阀口半径r_k位置处的变形量，等于等半径的单片阀片在阀口半径r_k位置的变形量，其中，阀口位置半径r_k等于不同外半径叠加阀片最大外半径r_b为特例。

1.不同外半径叠加阀片等效厚度计算

为了保证其特性保持不变，则必须保证在相同压力下，叠加阀片在阀口半径位置处的变形量等于等半径单片阀片的变形量。不同外半径叠加节流阀片等效厚度示意图如图5-23所示，其中h₁、h₂、h₃……h_n可以是单片的实际物理厚度，也可以是每组阀片的等效厚度。

图5-23 叠加阀片等效厚度示意图

（1）两组不同外半径节流阀片组成的叠加阀片 如图5-24所示，不同外半径的叠加阀片由两组叠加阀片组成，第一组叠加阀片等效厚度为h₁，外半径为r_b；第二组叠加阀片等效厚度为h₂，外半径为r_t，且r_t<r_b。根据第5.2.5节，两组叠加阀片重叠部分的等效厚度为h_E=h²₁+h²₂。可以将不同外半径的两组叠加阀片等效为外半径为r_b的单片节流阀片。

图5-24 两组不同外半径组成的叠加阀片等效厚度示意图

根据式（5-37），在均布压力下，两组不同外半径节流阀片组成的叠加阀片在阀口半径r_k位置处的变形量f_rk为

式中，G_rk为不同外半径节流阀片组成的叠加阀片在阀口半径r_k位置处的变形系数。

根据第4章可知，在均布压力下，等半径的单片节流阀片的在阀口半径r_k位置处的变形量f_rks为

式中，G_rks为等半径的单片节流阀片的在阀口半径r_k位置处的变形“长城”系数。

根据不同外半径的叠加阀片在阀口半径r_k位置处的变形量f_rk，等于等半径单片节流阀片在阀口半径r_k位置处的变形量f_rks，即f_rk=f_rks，因此有

由式（5-71），可得不同外半径的叠加阀片的等效厚度h_E为

定义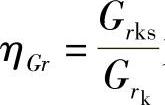为变形系数比，因此，式（5-72）可以表示为

（2）两片不同外半径节流阀片组成的叠加阀片 两片不同外半径节流阀片组成的叠加阀片，可以视为两组不同外半径节流阀片组成的叠加阀片的特例。在这种情况下，h₁为第一片节流阀片的物理厚度，h₂为第二片节流阀片的物理厚度，因此有。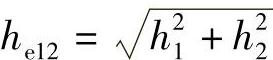

此时，由式（5-73）可知，两片不同外半径节流阀片组成的叠加阀片等效厚度h_E，也表示为

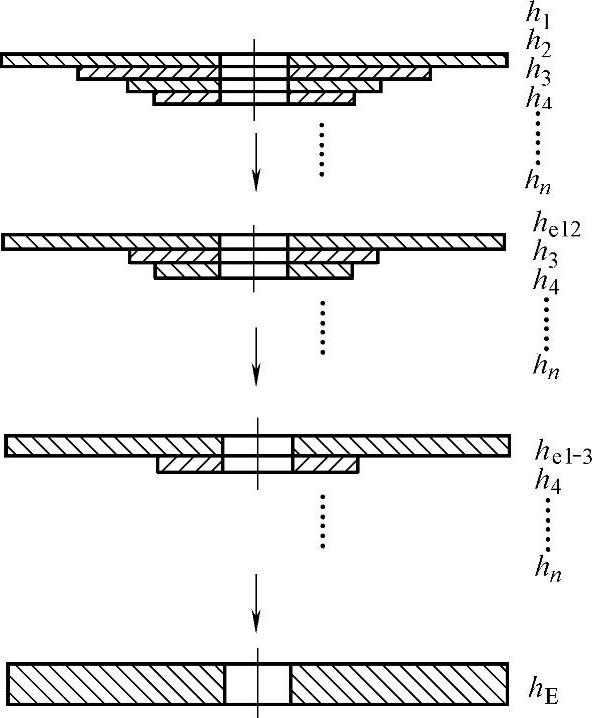
图5-25 多组不同外半径组成的叠加阀片等效厚度示意图

（3）多组不同外半径节流阀片组成的叠加阀片 多组不同外半径节流阀片组成的叠加阀片如图5-25所示，第1组至第n组阀片的等效厚度依次为h₁、h₂、h₃……h_i……h_n，即第i组等半径的叠加节流阀片的等效厚度为h_i，所对应的外半径依次为r_t1、r_t2、r_t3……h_ti……r_tn，其中r_t1等于阀片最大外半径r_b，内半径为r_a，阀口位置半径为r_k。

对于多组不同外半径节流阀片组成的叠加阀片等效厚度的计算，可以利用两组（两片）不同外半径节流阀片组成的叠加阀片的建模及其求解方法，解得阀片变形解析计算式，在建立等式求解通解中常数的时候，每多一组等半径的节流阀片就需要多4个连续性条件；在求得变形解析式后，利用两组（两片）不同外半径节流阀片组成的叠加阀片等效为等半径单片节流阀片的类似推导方法，可以导出多组不同外半径节流阀片组成的叠加阀片等效为等半径单片节流阀片的等效厚度计算公式。这里不再详细推导。

为了简化运算，满足实际工程的应用，下面根据等效原理，采用以下等效法进行计算。

首先，利用式（5-74）将第一组和第二组阀片等效为外半径为r_b的一片阀片，其厚度为h_e12。

然后，再利用式（5-74）将把厚度为h_e12、外半径为的r_b第一片阀片和第三组阀片等效为外半径为r_b的一片阀片，其厚度为h_e1-3，即h_e1-3为前三组的等效厚度。

依此类推，可得前i组的等效厚度h_e1-i，当i=n时，等效厚度h_e1-n为叠加阀片总的等效厚度h_E。

（4）多片不同外半径节流阀片组成的叠加阀片 如同两片不同外半径节流阀片组成的叠加阀片，可以视为两组不同外半径节流阀片组成的叠加阀片的特例一样，可以把多片不同外半径节流阀片组成的叠加阀片视为多组不同外半径节流阀片组成的叠加阀片的特例，从而求出等效厚度h_E。

2.等效厚度计算实例及验证

（1）等效厚度计算实例 某减振器由不同外半径的两组阀片叠加组成，如图5⁃22所示，有效内圆半径r_a=5.0mm；第一组阀片由两片组成，外圆半径r_b=8.5mm，厚度均为0.2mm；第二片阀片由两片组成，外半径r_t=7.0mm，第一片厚度为0.2mm，第二片为0.1mm；阀口半径r_k=8.5mm；阀片材料的弹性模型E=200GPa；泊松比μ=0.3。

根据式（5-5），可得第一组的等效厚度h_1e=0.251984mm，第二组的等效厚度h_2e=0.208008mm。

根据式（5-61），可得等效为等半径的单片节流阀片的厚度h₀=0.289798mm。

根据式（4-18），可得在均布载荷p=3.0MPa作用下，厚度为h₀=0.289798mm的单片节流阀片的在阀口半径r_k位置处的变形量f_rks为0.113857954004379mm。根据式（5-24），可得在均布载荷p=3.0MPa的作用下，两组不同外半径节流阀片组成的叠加阀片在阀口半径r_k位置处的变形量f_rk为0.113857954004379mm。由此可见，在相同压力下，两种模型的变形量相吻合。

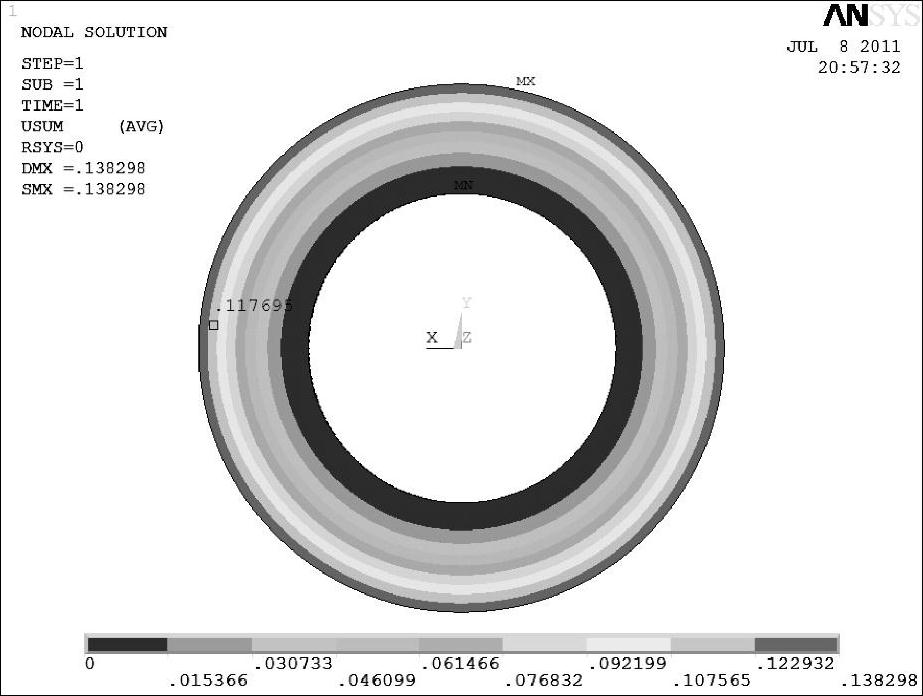
图5-26 节流阀片实际模型变形云图

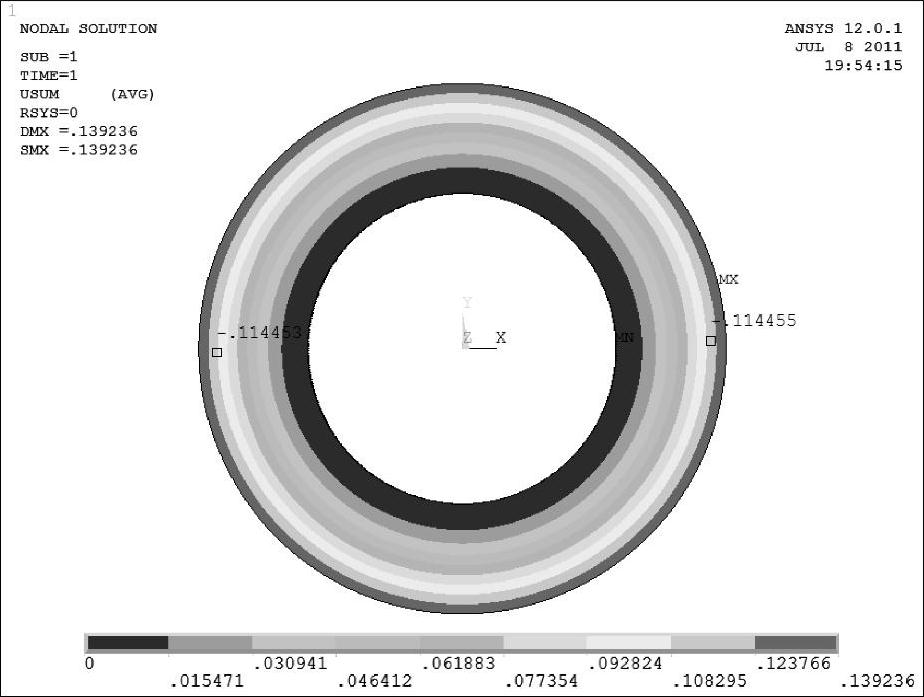
图5-27 节流阀片等效模型变形云图

（2）ANSYS仿真验证 利用AN⁃SYS有限元分析软件分别建立减振器节流阀片不同外半径实际模型及等效模型，分别如图5-9所示和图5-10所示，其边界条件与图中的力学模型一致。在建立模型之后，以0.1mm为单位对模型分别划分网格，对两个模型施加相同的均布载荷进行静力学变形仿真分析，仿真结果如图5-26和图5-27所示。

由图5-26和图5-27可知，不同外半径的叠加阀片在阀口r_k位置处的变形量为0.117695mm，等效的等半径单片节流阀片在阀口r_k位置处的变形量为0.114455mm，且都与变形解析值0.113857954004379mm相吻合。可见，叠加阀片的最大应力发生在较厚的阀片上。通过对比，结果表明所建立的不同外半径叠加阀片等效厚度计算方法是正确的，同时再一次验证了不同外半径叠加阀片变形解析计算方法及等半径节流阀片解析计算方法是正确可靠的。

3.不同外半径叠加阀片等效拆分设计

为了满足应力强度和阀片系列批量加工要求，可以将原等半径的单片设计厚度阀片拆分设计为多片不同外半径的叠加阀片，如图5⁃28示。

图5⁃28 阀片拆分设计为叠加阀片示意图

一组（可以是单片）等半径的节流阀片拆分为不同外半径的叠加阀片是等效厚度计算的逆过程，依据同样是这组（可以是单片）等半径的节流阀片在阀口半径r_k位置处的变形量，等于不同外半径的叠加阀片在阀口半径r_k位置处的变形量。

（1）拆分为两组不同外半径节流阀片组成的叠加阀片 如图5-29所示，根据两组叠加阀片重叠部分的等效厚度h_e=h²_1e+h²_2e。一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片，可以拆分为两组不同外半径节流阀片组成的叠加阀片。第一组叠加阀片等效厚度为h_1e，外半径为r_b；第二组叠加阀片等效厚度为h_2e，外半径为r_t，且r_t<r_b。

(www.daowen.com)

图5-29 拆分为两组不同外半径组成的叠加阀片示意图

拆分设计所得的第一组的叠加阀片等效厚度为h_1e，且h_1e<h₀。此时，不同外半径节流阀片的变形系数看作厚度比_ηh的函数，即G_rk=G_rk（η_h）根据式（5-71），可得

由式（5-36）可得阀口位置r_k处的变形系数为

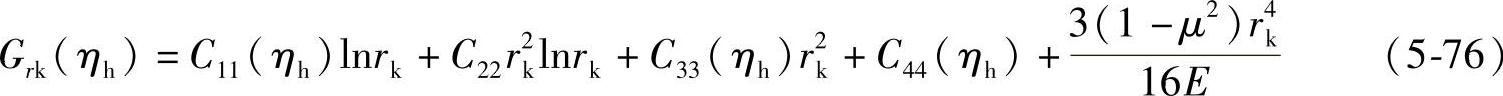
由式（5-75）和（5-76），可得

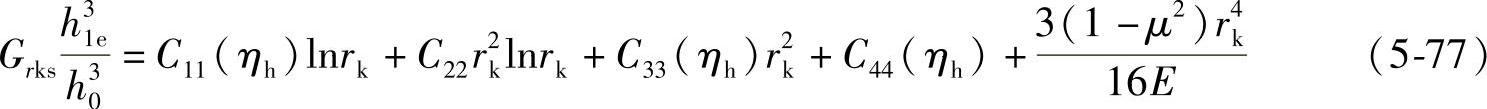
式中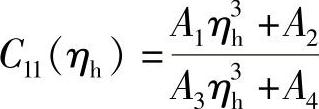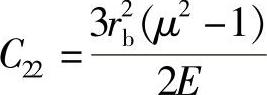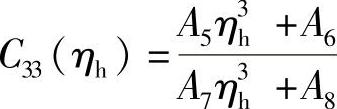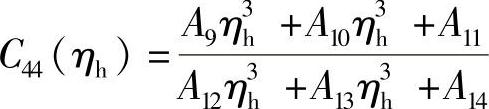，，，，，其中，A₁、A2……A₁₄均是由E、μ、r_a、r_b及r_t决定的常数。

令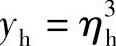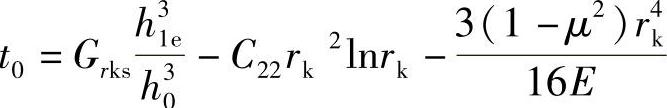，，由式（5-77）可得

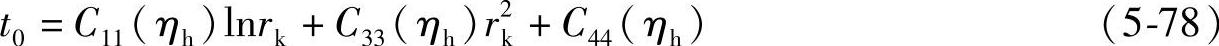
即

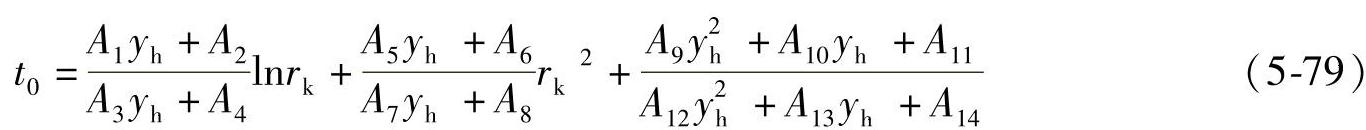
整理式（5-79），可得关于y_h的4次方程，即

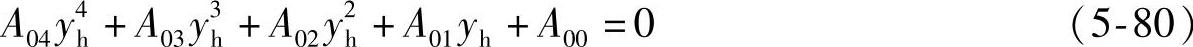
式中，A₀₄=-t₀A₃A₇A₁₂+lnr_kA₇A₁A₁₂+r²_kA₅A₃A₁₂+A₃A₇A9

A₀₃=-t₀（A₃A₇A₁₃+A₁₂A₈A3+A₁₂A4 A7）+lnr_k（A₂A₇A₁₂+A₈A₁A₁₂+A₇A₁A₁₃）+r²_k（A₄A₅A₁₂+A₆A₃A₁₂+A₅A₃A₁₃）+（A₄A₇A₉+A₈A₃A₉+A₃A₇A₁₀）

A₀₂=-t₀（A₃A₇A₁₄+A₄A₈A₁₂+A₈A₃A₁₃+A₄A₇A₁₃）+lnr_k（A₂A₇A₁₃+A₈A₁A₁₃+A₇A₁A₁₄+A₈A₂A₁₂）+r²_k（A₄A₅A₁₃+A₆A₃A₁₃+A₁₄A₅A₃+A₆A₄A₁₂）+（A₄A₇A₁₀+A₈A₃A₁₀+A₃A₇A₁₁+A₄A₈A₉）

A₀₁=-t₀（A₈A₃A₁₄+A₄A₇A₁₄+A₄A₈A₁₃）+lnr_k（A₂A₇A₁₄+A₈A₂A₁₃+A₈A₁A₁₄）+r²_k（A₄A₅A₁₄+A₆A₃A₁₄+A₆A₄A₁₃）+（A₄A₇A₁₁+A₈A₃A₁₁+A₄A₈A₁₀）

A₀₀=-^t₀A4 A8 A14+lnrk A8 A2 A14+r2k A6 A4 A14+A4 A8 A11

由式（5-80），利用计算机程序可以求得y_h，即可得厚度比。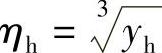

根据厚度比的定义可得

把根据式（5-80）可求得的厚度比η_h代入式（5-81），可得第二组叠加节流阀片的厚度为

h_2e=η_hh_1e （5-82）

（2）拆分为两片不同外半径节流阀片组成的叠加阀片 一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片，拆分为两片不同外半径节流阀片组成的叠加阀片，可以一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片拆分为两组不同外半径节流阀片组成的叠加阀片的特例。在这种情况下，第一组叠加阀片等效厚度h_1e为第一片节流阀片的厚度，即h_1e=h₁；第二组叠加阀片等效厚度h_2e为第二片节流阀片的厚度，即h_2e=h₂。

首先拆分设计得到第一片节流阀片厚度h₁，且h₁<h₀。

然后，利用式h₂=η_hh₁求得第二片节流阀片的厚度h₂。

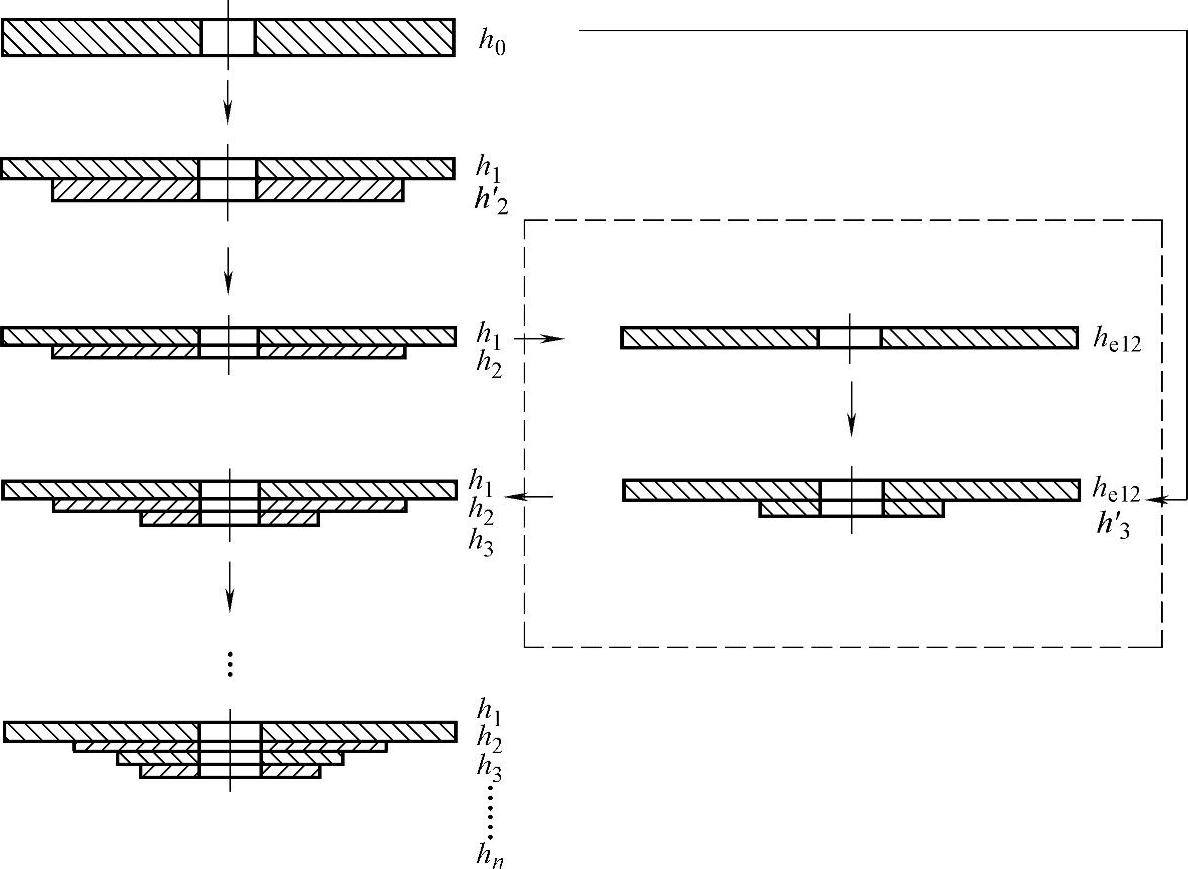
图5-30 拆分设计示意图

（3）拆分为多组不同外半径节流阀片组成的叠加阀片 如图5-30所示，一组（可以为单片）外半径为r_b且等效厚度为h₀的节流阀片，可以拆分为多组不同外半径节流阀片组成的叠加阀片，且第一组至第n组阀片的等效厚度依次为h₁、h₂、h₃……h_i……h_n，即第i组等半径叠加节流阀片的等效厚度为h_i，所对应的外半径依次为r_t1、r_t2、r_t3……h_ti……r_tn，其中r_t1等于阀片最大外半径r_b，内半径都为r_a，阀口位置半径为r_k。

可以首先根据拆分的组数建立不同外半径叠加节流阀片微分方程并及求得变形解析式；在求得变形解析式后，利用一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片拆分为两组不同外半径节流阀片组成的叠加阀片的推导方法，即可以导出拆分设计公式。这里不再详细推导。

为了简化运算，满足实际工程的应用，下面根据等效原理，采用以下等效法进行拆分设计。

第一步，根据外半径为r_b及节流阀片厚度h₀，在阀片系列中选取外半径为r_t1=r_b的一组阀片，且这组阀片的等效厚度为h₁，其中h₁<h₀。

第二步，根据阀片外半径r_b，确定第二组阀片外半径r_t2，且r_t2<r_t1；再根据阀片阀口r_k位置处变形相等，利用式（5-74）可得虚拟阀片厚度h₂′，根据第二组阀片厚度小于等于虚拟阀片厚度h₂′，从而确定第二组阀片厚度h₂。

第三步，根据第二组阀片外半径r_t2，确定第二组阀片外半径r_t3，且r_t3<r_t2；利用式（5-82）把第一组和第二组阀片等效为外半径为r_b且厚度为h_e12的一片阀片，再利用式（5-74）及参数h₀和h_e12确定虚拟阀片厚度h′₃；根据第三组阀片厚度小于等于h′₃，从而确定第三组阀片厚度h₃。

依此类推，可把一组（可以为单片）外半径为r_b且等效厚度为h₀的节流阀片，拆分为n组不同外半径节流阀片组成的叠加阀片。

（4）拆分为多片不同外半径节流阀片组成的叠加阀片 一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片，拆分为多片不同外半径节流阀片组成的叠加阀片，可以一组（可以为单片）外半径为r_b且厚度为h₀的节流阀片拆分为多组不同外半径节流阀片组成的叠加阀片的特例。

4.拆分设计实例及仿真验证

（1）拆分设计实例一与ANSYS仿真验证 某节流阀片单片设计厚度为h₀=0.30mm，有效内圆半径r_a=5.0mm，外半径r_b=8.5mm，阀口半径r_k=8.0mm；阀片材料的弹性模型E=200GPa；泊松比μ=0.3。

根据不同外半径叠加阀片拆分设计方法，可得拆分设计结果为：第一片节流阀片厚度h₁=0.25mm，外半径r_b=8.5mm；第二片节流阀片厚度h₂=0.2mm，外半径r_t2=7.0mm；第三片节流阀片厚度h₃=0.178473976512616mm，外半径r_t3=6.0mm。

为了验证拆分设计方法的正确性，第三片节流阀片厚度没有圆整。利用第4章中阀片在均布压力下的变形解析计算式，可得实例中单片设计厚度为h₀=0.30mm的阀片在均布压力3.0MPa作用下，阀口位置r_k=8.0mm处变形解析值为0.1026mm。

利用ANSYS有限元分析软件建立减振器节流阀片不同外半径的实际模型，其边界条件与图5⁃9中的力学模型一致。在建立模型之后，以0.1mm为单位对模型分别划分网格，对模型施加3.0MPa均布载荷进行静力学变形仿真分析，仿真结果如图5-31所示。

由图5-31可知，在阀口半径r_k=8.0mm圆周上的变形值为0.10346mm，与实例中单片设计厚度为h₀=0.30mm的阀在相同均布压力下的变形解析值相吻合，相对偏差仅为0.838%。通过对比，表明所建立的不同外半径叠加阀片拆分设计方法是正确的。

（2）拆分设计实例二与ANSYS仿真验证 某节流阀片单片设计厚度为h₀=0.30mm，有效内圆半径r_a=5.0mm，外半径r_b=8.5mm；阀口半径r_k=8.5mm；阀片材料的弹性模型E=200GPa；泊松比μ=0.3。

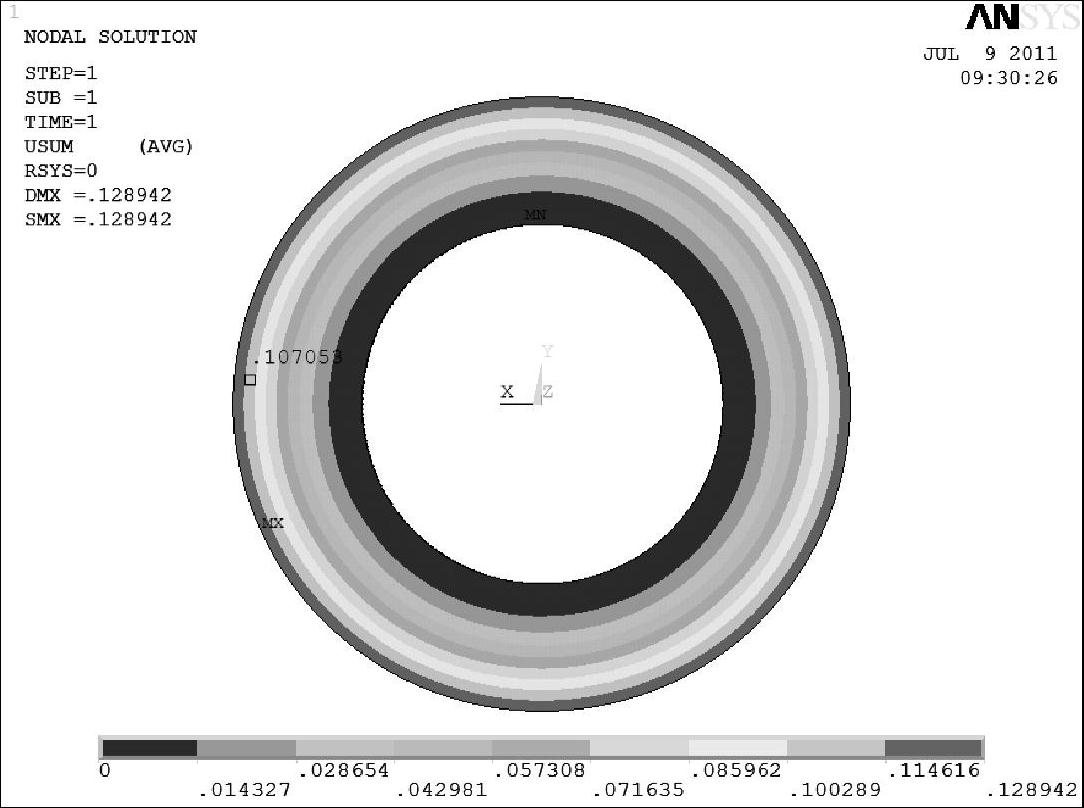
图5-31 节流阀片变形云图

根据不同外半径叠加阀片拆分设计方法，可得拆分设计结果为：第一片节流阀片厚度h₁=0.25mm，外半径r_b=8.5mm；第二片节流阀片厚度h₂=0.2mm，外半径r_t2=7.0mm；第三片节流阀片厚度h₃=0.169541282530516mm，外半径r_t3=6.5mm。

为了验证拆分设计方法的正确性，第三片节流阀片厚度同样没有圆整。利用式（4-5），可得实例中单片设计厚度为h₀=0.30mm的阀片在均布压力3.0MPa的作用下，阀口位置r_k=8.5mm处变形解析值为0.1248mm。

利用ANSYS有限元分析软件建立减振器节流阀片不同外半径实际模型，其边界条件与图5-7中的力学模型一致。在建立模型之后，以0.1mm为单位对模型分别划分网格，对模型施加3.0MPa均布载荷进行静力学变形仿真分析，仿真结果如图5-32所示。

图5-32 节流阀片变形云图

由图5-32可知，在阀口半径r_k=8.5mm圆周上的变形量为0.127076mm，与实例中单片设计厚度为h₀=0.30mm的阀在相同均布压力下的变形解析值相吻合，相对偏差仅为1.75%。通过对比，表明所建立的不同外半径叠加阀片拆分设计方法是正确的。

其中，实例二是阀口位置半径r_k等于不同外半径叠加阀片最大外半径r_b的情况。