1.不同外半径叠加节流阀片的应力数学模型

（1）等效叠加节流阀片所受内力及应力 不同外半径叠加节流阀片等效模型所受的内力主要是径向弯矩M_r和周向弯矩M_θ，根据第3章中阀片内力与变形之间关系，叠加节流阀片所受总的内力矩M_r和M_θ可分别表示为

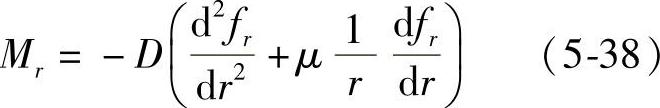
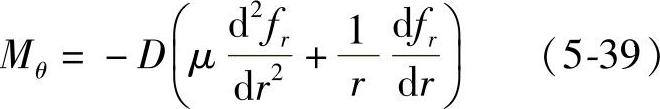
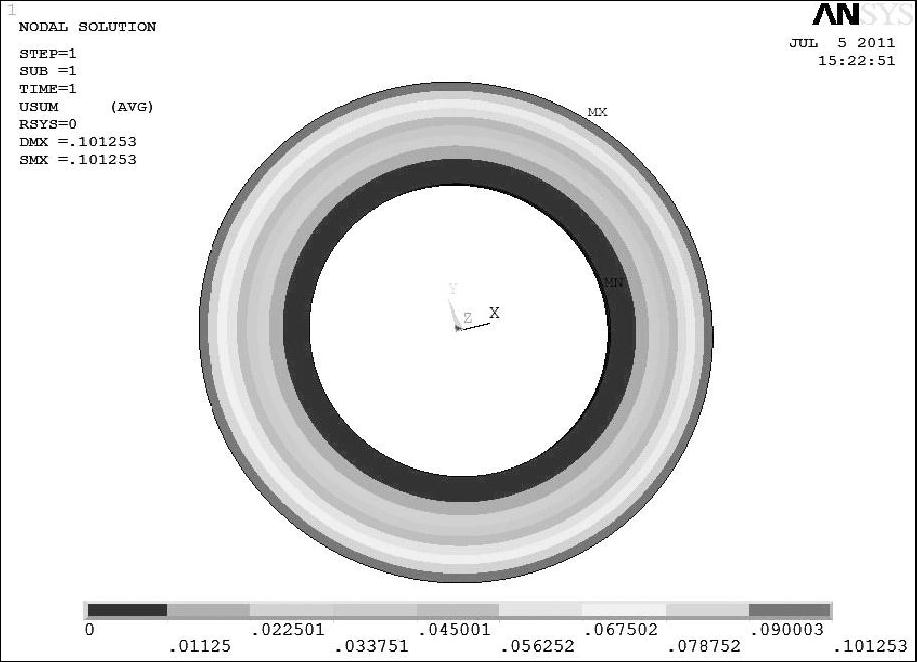
图5-16 节流阀片等效模型变形云图

将式（5-37）分别代入两式（5-38）和式（5-39），并代入D的表达式，整理可得

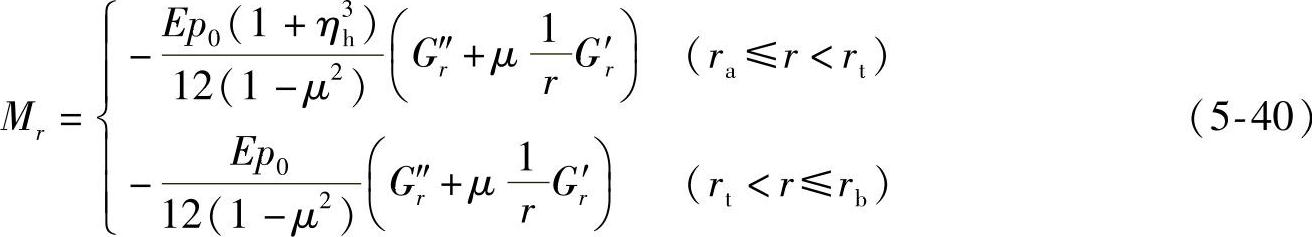
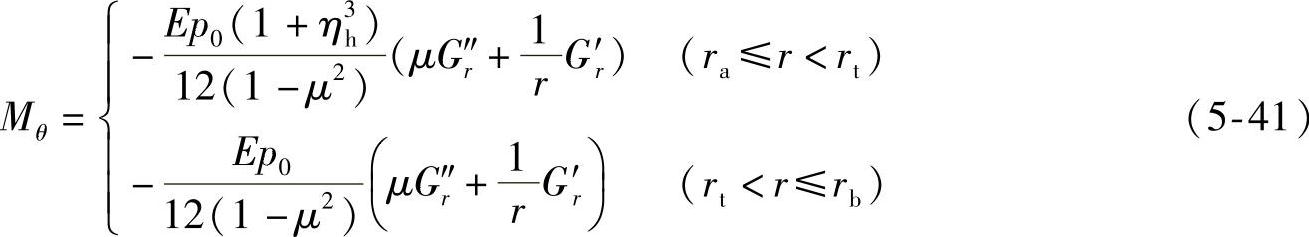
式中，G′_r和G″_r分别表示阀片变形“长城”系数G_r的一阶导数和二阶导数。

若在r_a<r≤r_t上，两片阀片等效为一片阀片时，则阀片在半径r位置上、下表面（z=±h/2，z为阀片轴向位置坐标）处的应力最大，且上、下表面上的径向应力和周向应力，可分别表示为

将式（5-40）和式（5-41）分别代入式（5-42）和式（5-43），可得

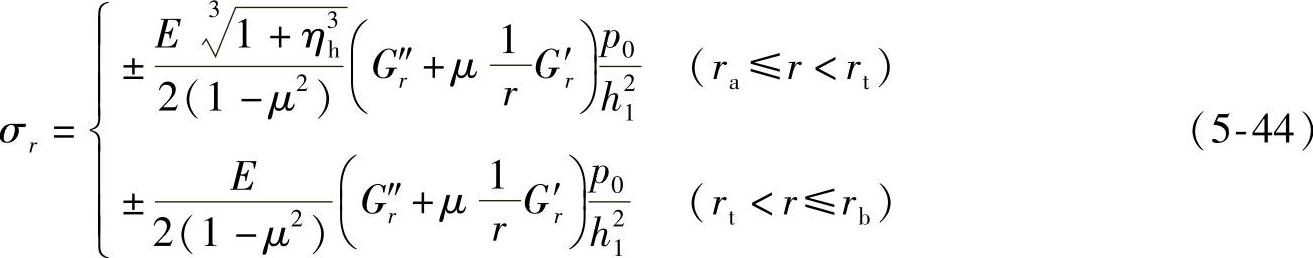
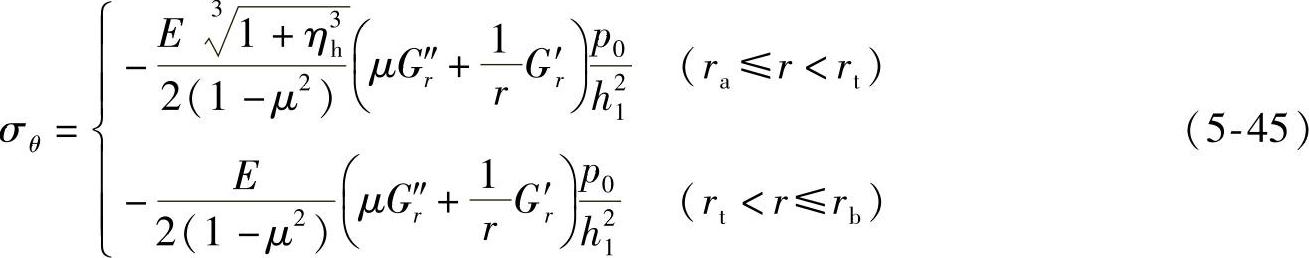
令

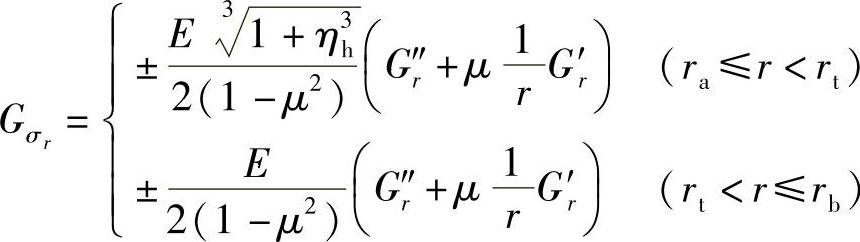
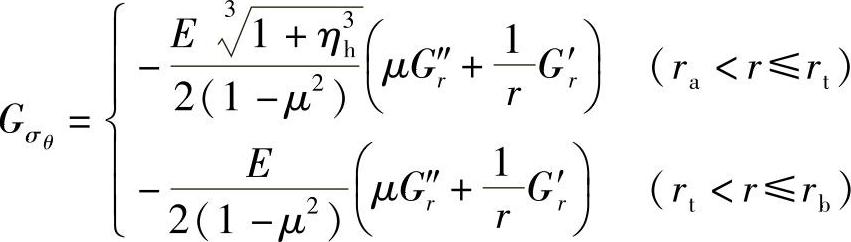
因此，式（5-44）和式（5-45）分别表示为

式中，G_σr为阀片径向应力“长城”系数；G_σθ为周向应力“长城”系数。其物理意义分别为单位厚度阀片在单位压力作用下，阀片在位置半径r的上、下表面处的径向和周向应力的大小，单位为m²或mm²。阀片应力系数随半径变化的曲线如图5-17所示。

需要说明的是，由于在r_t处，节流阀片厚度发生突变，因此，应力系数G_σr和G_σθ在r_t处不连续。

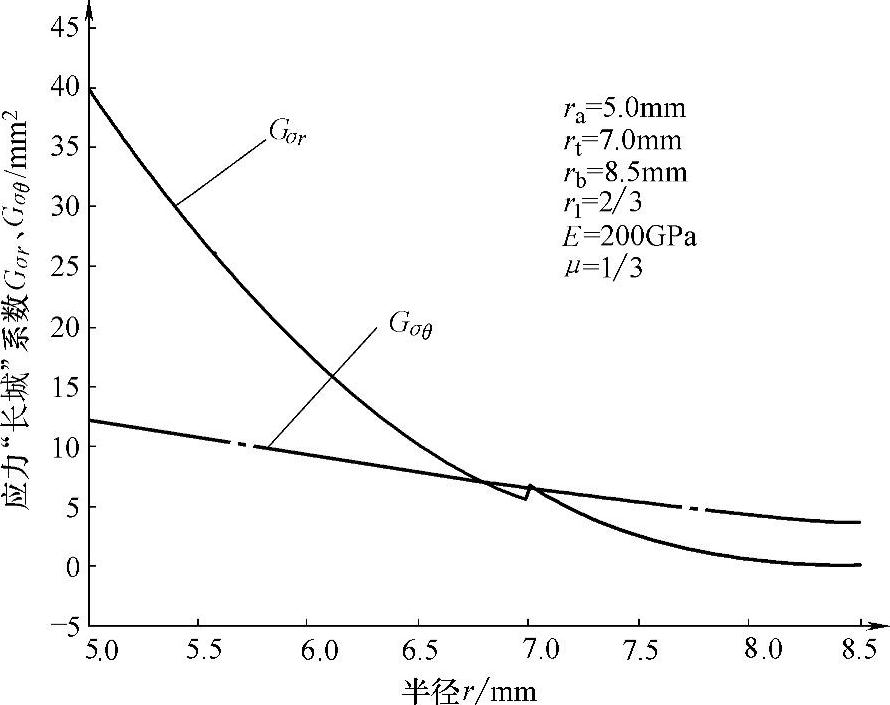
图5-17 阀片应力“长城”系数随半径变化的曲线

由于等效叠加阀片主要受径向和周向应力，因此，根据第四强度理论，节流阀片的复合应力为

（2）第一片节流阀片所受内力及应力 根据叠加原理，且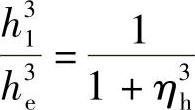，因此第一片节流阀片所受的内力M_1r和M_1θ可分别表示为

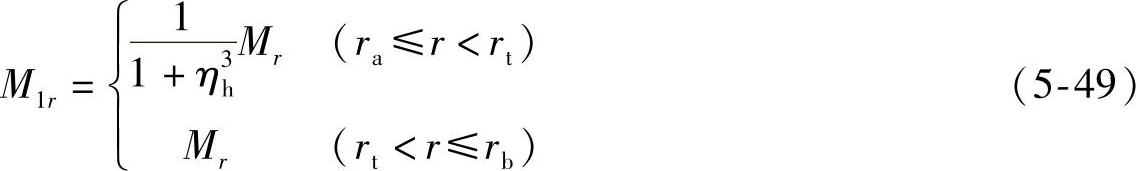
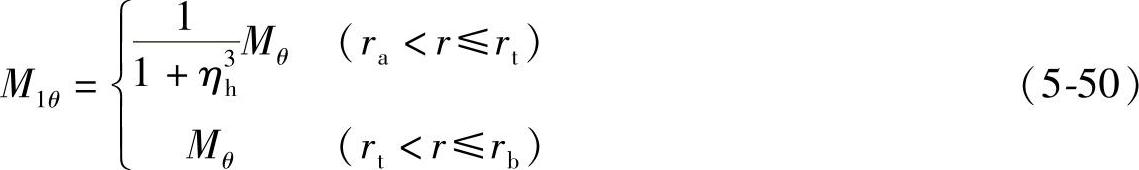
将叠加节流阀片所受总的内力M_r和M_θ代入式（5-49）和式（5-50），即可求得第一片节流阀片所受的内力M_1r和M_1θ。

节流阀片在半径r位置上、下表面（z=±h/2，z为阀片轴向位置坐标）处的径向应力和周向应力分别为

将式（5-49）和式（5-50）分别代入式（5-51）和式（5-52），可得

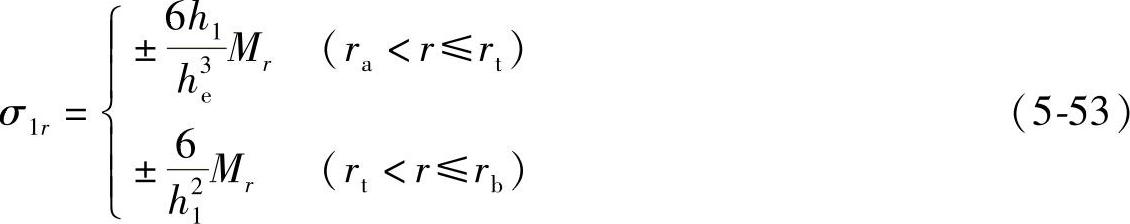
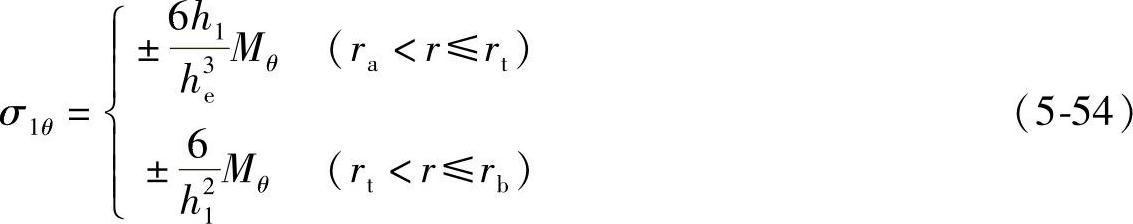
将式（5-40）和（5-41）代入式（5-53）和式（5-54）可得

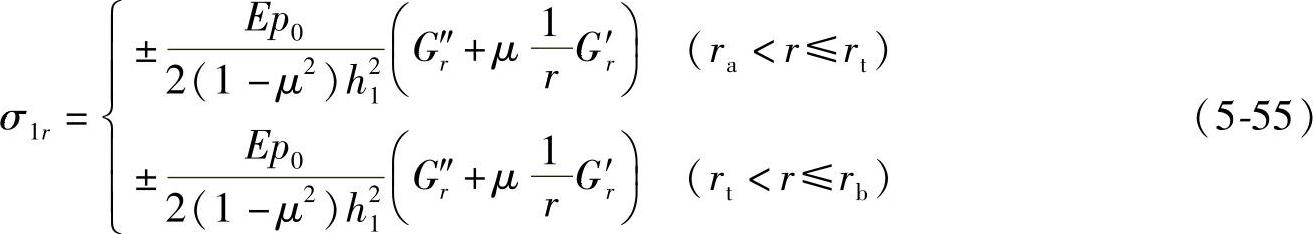
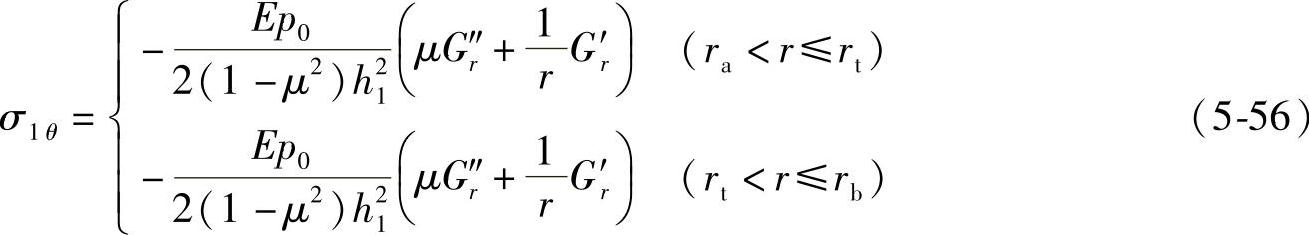
利用G_σr及G_σθ化简式（5-55）和式（5-56），可得(www.daowen.com)

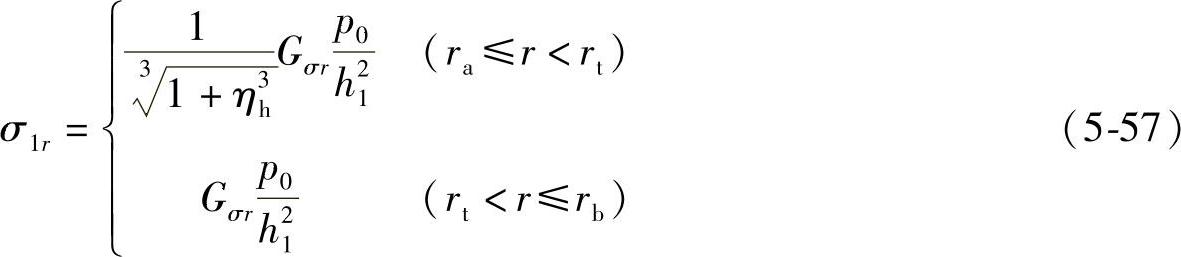
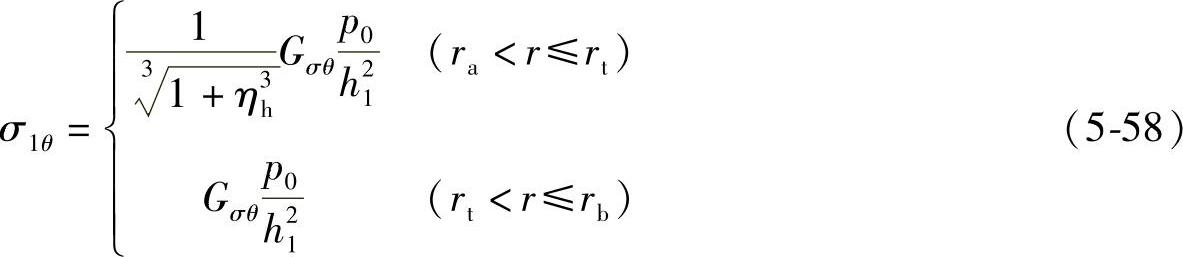
由式（5-57）和式（5-58）可知，σ_1r及σ_1θ与σ_r及σ_θ的关系为

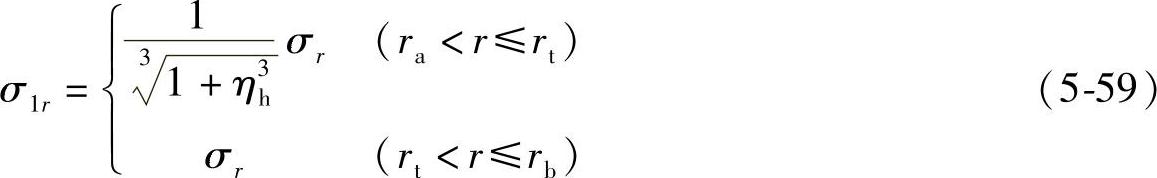
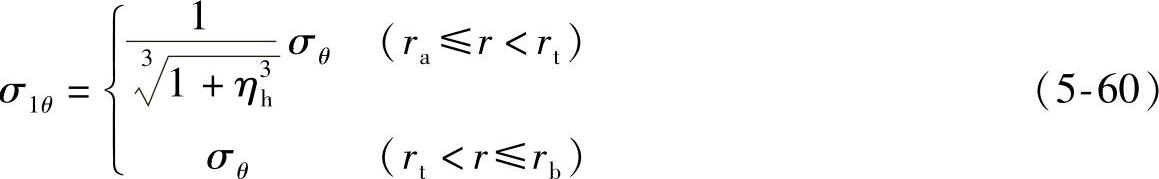
第一片节流阀片主要受径向和周向应力作用，因此，据第四强度理论，阀片复合应力为

将式（5-59）和式（5-60）代入式（5-61），可得

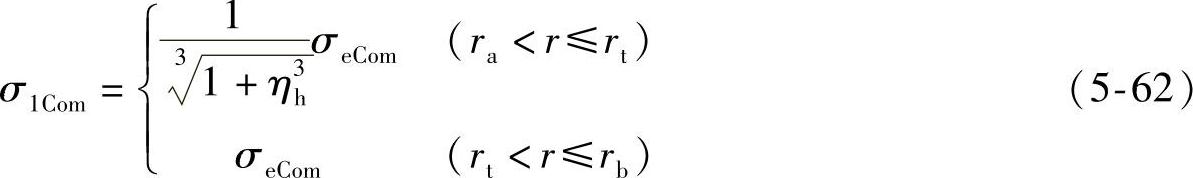
（3）第二片节流阀片所受内力和应力 根据叠加原理，且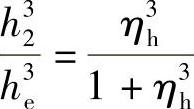，因此，第二片节流阀片所受的内力M_2r和M_2θ可分别表示为

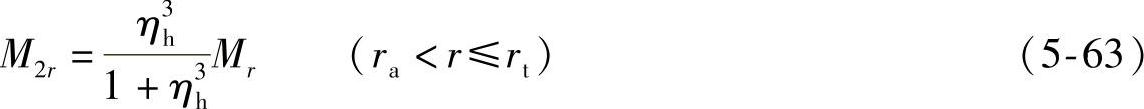
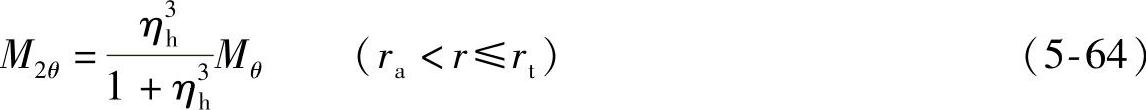
同理，第二片节流阀片所受的内力σ_2r和σ_2θ可分别表示为

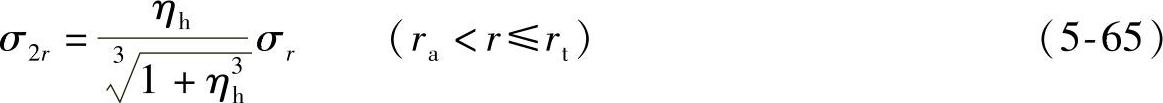
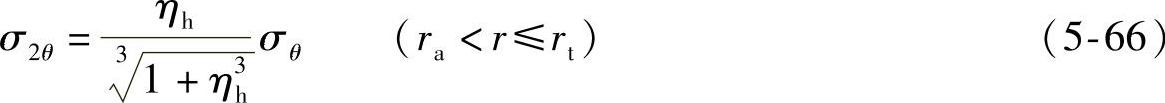
第一片节流阀片主要受径向和周向应力作用，因此，据第四强度理论，阀片复合应力为

将式（5-65）和式（5-66）代入式（5-67），可得

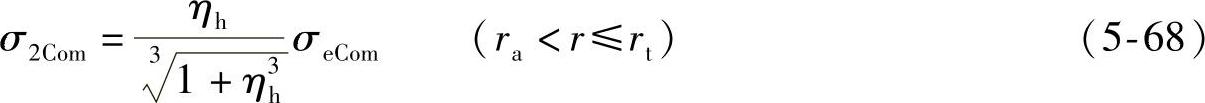
对于多片（或多组）不同外半径叠加阀片的应力计算，得出的结论也与外圆边界受弯矩和剪力的叠加节流阀片的应力完全相同，只是多片（或多组）不同外半径叠加阀片的应力系数与厚度比η_h有关，这里不再详细推导。

两片不同外半径阀片叠加是多片（或多组）不同外半径叠加阀片的特例，与外圆边界受弯矩和剪力的叠加节流阀片一样，这两片阀片的应力系数分别等于它们的厚度系数。因此有

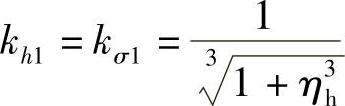
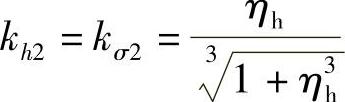
2.阀片应力计算实例

某减振器节流阀片由两片组成，如图5⁃9所示，有效内圆半径r_a=5.0mm，第一片阀片外圆半径r_b=8.5mm，厚度h₁=0.3mm；第二片阀片外半径r_t=7.0mm，厚度h₂=0.2mm；阀口半径r_k=8.5mm。阀片材料的弹性模型E=200GPa；泊松比μ=0.3。在均布载荷p=3.0MPa的作用下，各片节流阀片及等效节流阀片应力随半径r的变化曲线如图5-18所示，第一片和第二片节流阀片各应力随半径r的变化曲线分别如图5-19和图5-20所示。

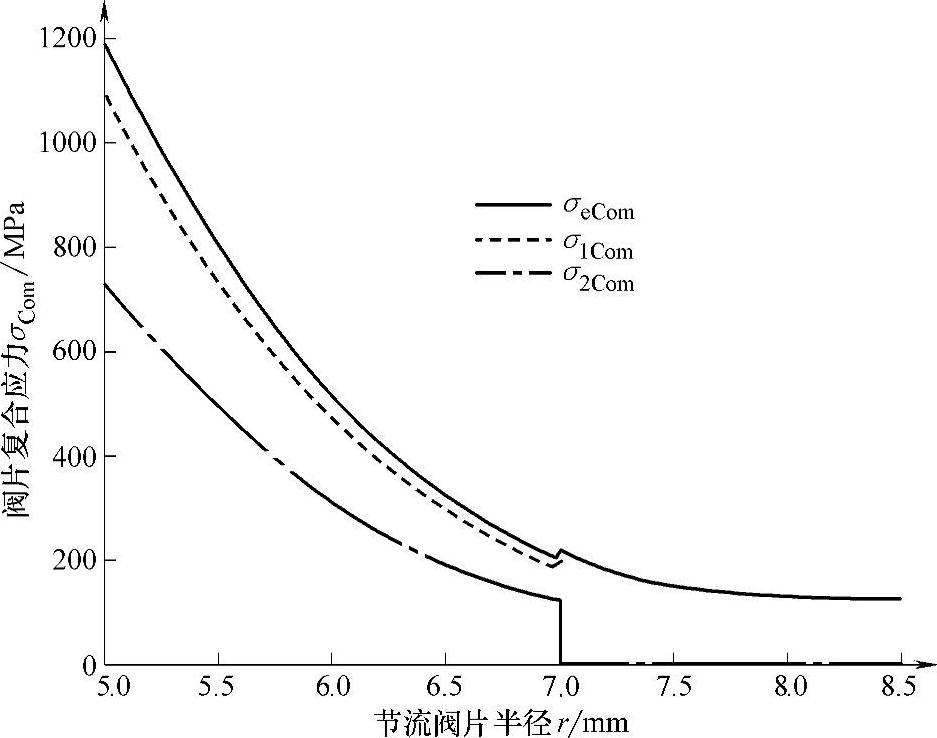
图5-18 节流阀片应力随半径变化曲线

由图5-18可知，等效节流阀片最大复合应力σ_{eCom max}=1196.09MPa；第一片节流阀片最大复合应力σ_{1Com max}=1096.97MPa；第二片节流阀片最大复合应力σ_{2Com max}=731.31MPa。采用叠加阀片使得阀片的最大复合应力降低了99.12MPa，因此，采用叠加阀片可以明显降低阀片应力，提高阀片使用寿命。

利用解析计算方法，可以得到第一片节流阀片最大径向应力σ_{1 rmax}=1234.19MPa，最大周向应力σ_{1 θmax}=370.26MPa，最大复合应力σ_{1 Com max}=1096.97MPa。

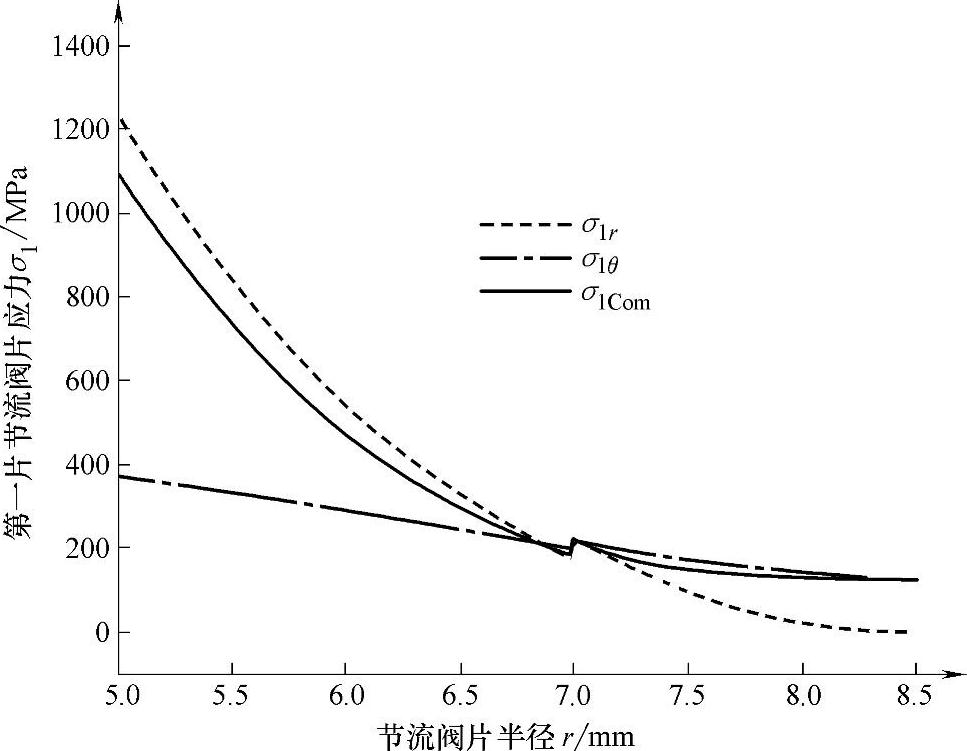
图5-19 第一片节流阀片应力随半径变化曲线

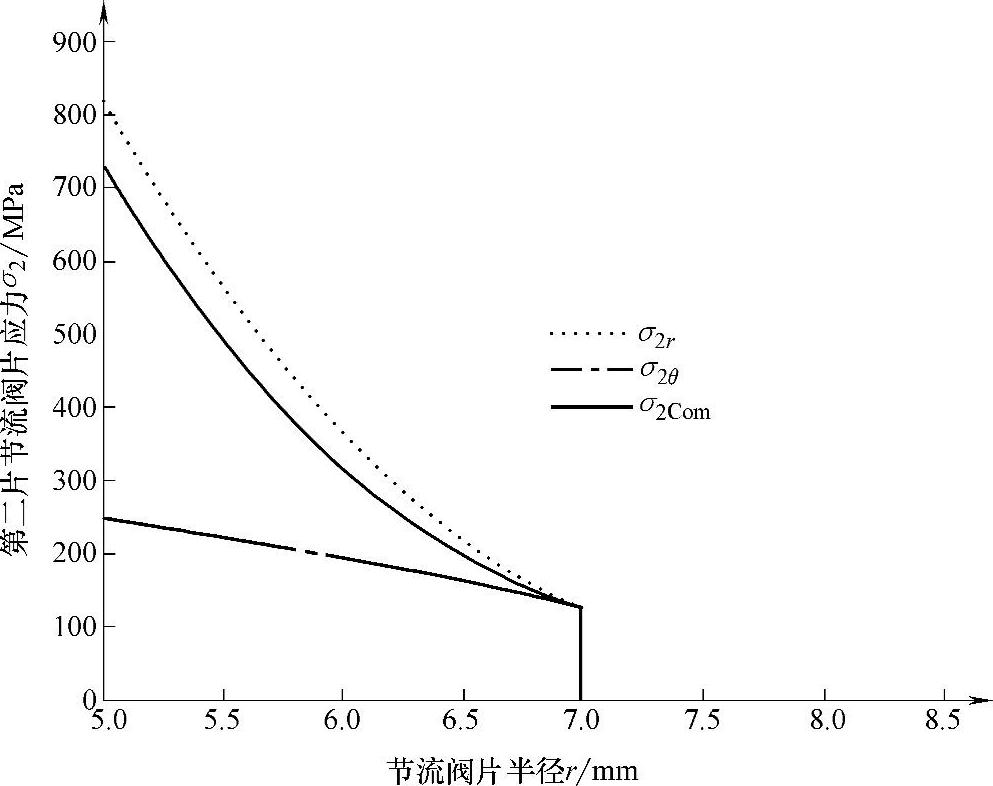
图5-20 第二片节流阀片应力随半径变化曲线

利用解析计算方法，可以得到第二片节流阀片最大径向应力σ_{2 rmax}=822.79MPa，最大周向应力σ_{2 θmax}=246.84MPa，最大复合应力σ_{2Com max}=731.31MPa。

需要说明的是，在r_t处，由于节流阀片厚度发生突变，导致阀片应力在r_t处不连读，如图5-16和图5-17所示，但是在r_t处的变形、转角（变形斜率）、剪切力及弯矩是连续的。

3.ANSYS软件数值仿真验证

对于上述节流阀片，利用ANSYS有限元分析软件建立模型，其边界条件及力学模型与图5⁃7的一致，以0.1mm为单位对模型划分网格，在半径r=[5.0，8.5]mm区间上施加均布压力3.0MPa，对阀片进行静力学应力仿真分析，仿真结果如图5-21所示。

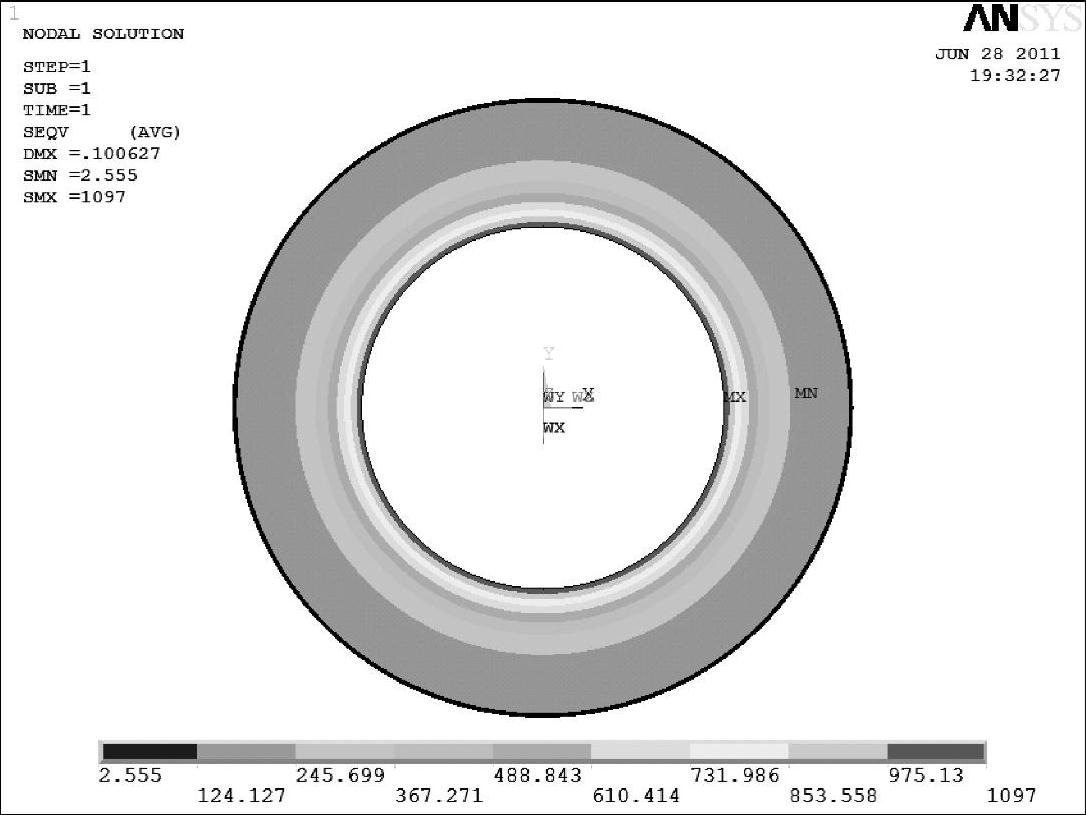
图5-21 阀片应力仿真云图

由图5-21可知，利用AN⁃SYS有限元仿真分析软件，对不同外半径叠加阀片在均布力下的应力进行数值仿真分析，所得到的第一片阀片最大复合应力为1097MPa，与利用解析计算得到的第一片最大复合应1096.97MPa相吻合，相对偏差仅为0.00255%；仿真得到的阀片最大复合应力为731MPa，与利用解析计算得到的第二片最大复合应731.31MPa相吻合，相对偏差仅为0.04241%，可见，叠加阀片的最大应力发生在较厚的阀片上。通过对比，可表明所建立的不同外半径叠加阀片应力解析计算方法是正确的。