将8个通解常数代入式（5-27），可得在均布压力作用下不同外半径叠加节流阀片在任意半径r处的变形解析式。

为了化简变形解析式，令h₂=η_hh₁，其中将η_h定义为厚度比。阀片变形解的各项都含有一个公因子p₀/h³₁，对式（5-27）提取公因子p₀/h³₁，将剩余项归结为G_r，则有

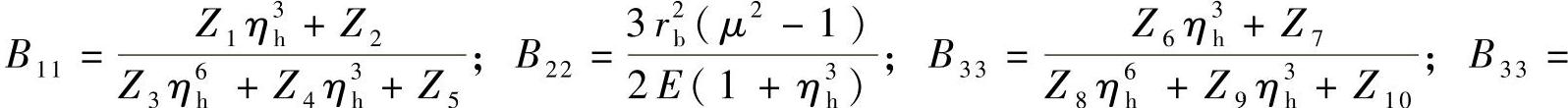
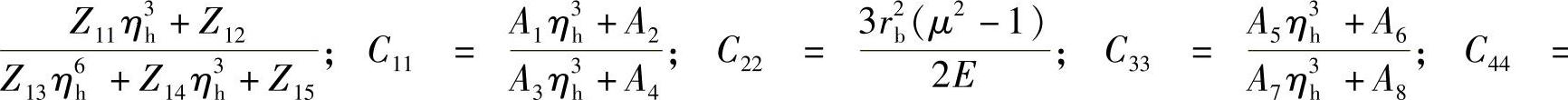
式中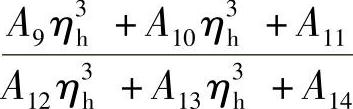，。其中，Z₁、Z₂……Z₁₅及A₁、A₂……A₁₄均是由E、μr_a、r_b及r_t决定的常数。因此，不同外半径阀片叠加，在半径r位置处的变形系数，则阀片在半径r处的变形量可表达为

式中，G_r为阀片在线性均布压力作用下，在半径r处的变形系数，即阀片变形“长城”系数。它不仅与阀片的结构、弹性模型、泊松比、半径位置有关，还与两片阀片厚度比η_h及线性非均布载荷的加载位置有关，其单位为m⁶/N或mm⁶/N。

例如，某叠加节流阀片由两片组成，内半径都为r_a=5.0mm；第一片外半径r_b=8.5mm；第二片节流阀片外半径r_t=7.0mm；阀口位置半径r_k=8.0mm；厚度比η_h=2/3；阀片材料的弹性模型E=200GPa；泊松比μ=0.3。该节流阀片在均布压力作用下的变形“长城”系数如图5-11所示。

由此可知，阀片在均布载荷作用下，其阀片变形“长城”系数G_r随半径r而变化。(www.daowen.com)

阀口位置半径r_k=8.0mm处的变形系数G_rk随厚度比η_h的变化曲线，如图5-12所示。

由图5-12可知，随着厚度比η_h的增大，阀口位置半径r_k处的变形系数G_rk逐渐减小。

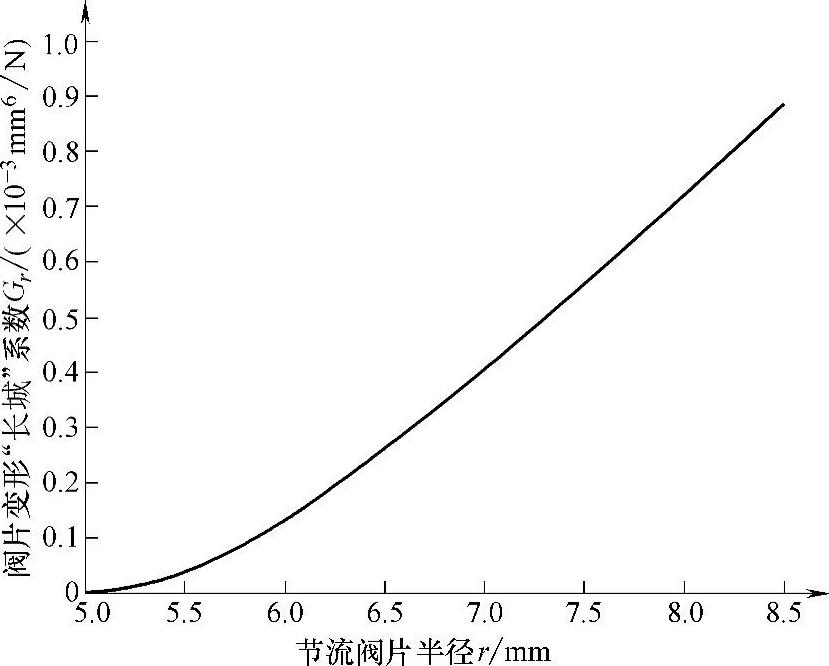
图5-11 阀片变形“长城”系数曲线

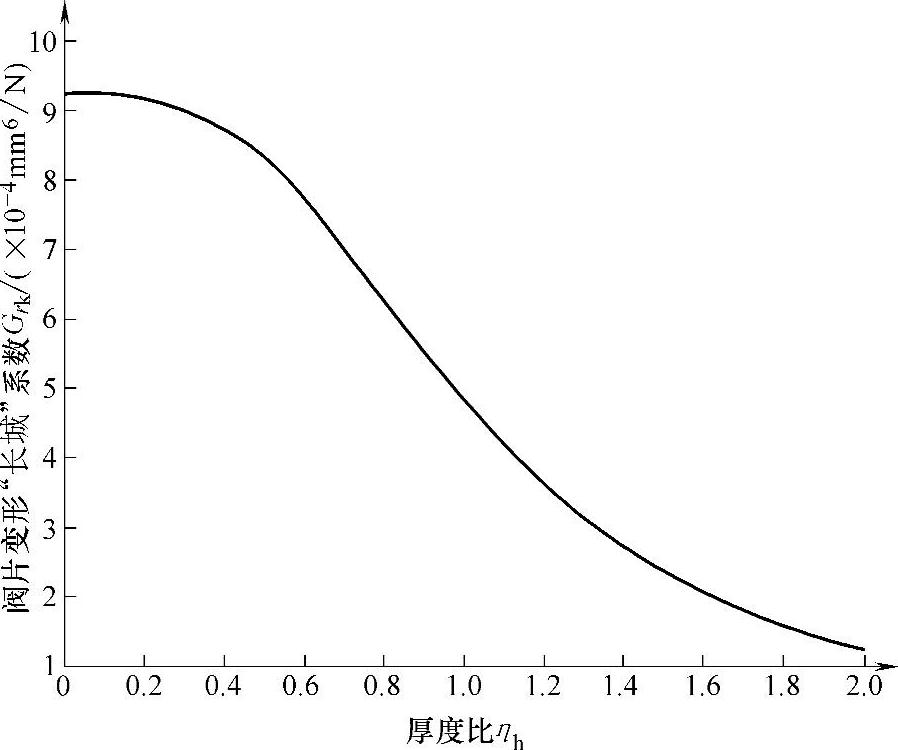
图5-12 阀片变形“长城”系数随厚度比的变化曲线