1.变厚度节流阀片在均布压力下的应力解析计算实例

根据变厚度阀片应力“长城”系数和应力的解析计算式，可求得阀片在位置半径r处的径向应力、周向应力和复合应力。此方法称为变厚度阀片应力“长城”系数法。

例如，某减振器变厚度节流阀片，弹性模量E=200GPa，泊松比μ=1/3；有效内圆半径r_a=5.0mm，外圆半径r_b=8.5mm，阀口半径r_k=8.5，变厚度半径r_t=7.3mm；在均布载荷p=3.0MPa作用下，变厚度阀片应力随半径r的变化曲线如图4-37所示。

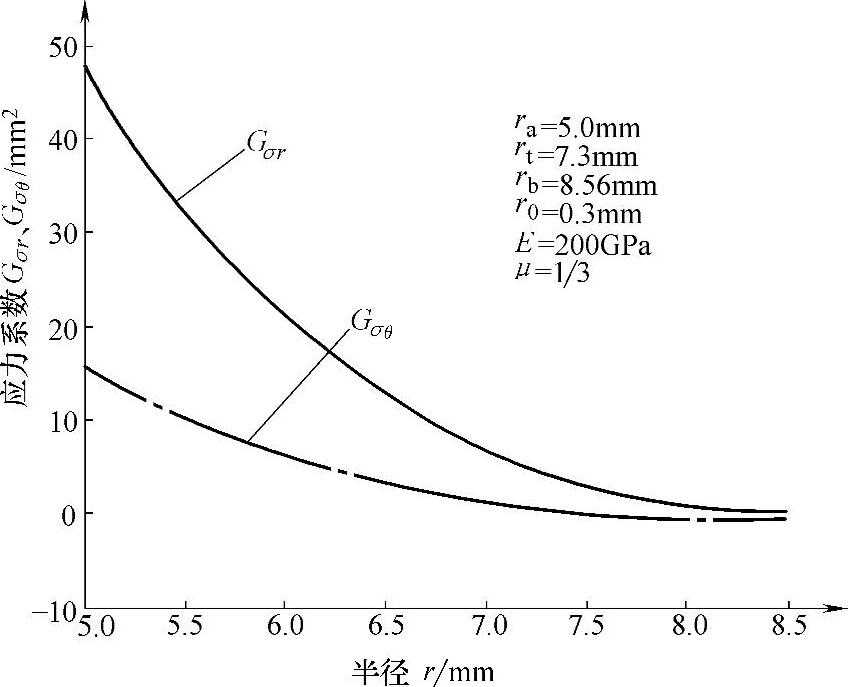
图4-36 变厚度阀片应力系数随半径变化的曲线

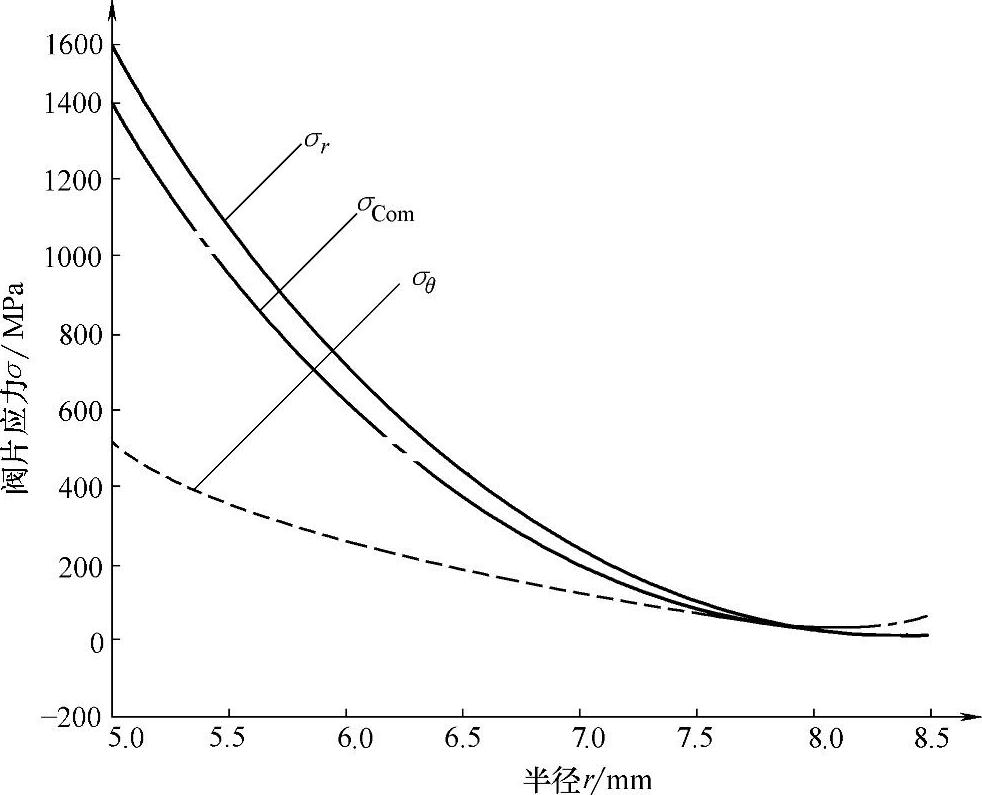
图4-37 变厚度阀片应力系数随半径变化的曲线

利用变厚度阀片应力“长城”系数法进行解析计算，可以得到阀片最大径向应力σ_rmax=1589.19MPa，最大周向应力σ_θmax=529.73MPa，最大复合应力σ_Commax=1401.53MPa。(www.daowen.com)

2.ANSYS软件数值仿真验证

对于上述变厚度节流阀片，利用ANSYS有限元分析软件建立模型，其边界条件与图4-32的力学模型一致，以0.1mm为单位对模型划分网格，在半径r=[5.0，8.5]mm区间上施加均布压力3.0MPa，对阀片进行静力学应力仿真分析。仿真结果如图4-38所示。

由图4-38可知，利用ANSYS有限元仿真分析软件对变厚度阀片在均布压力下的应力进行数值仿真分析，所得到的阀片最大复合应力为1390MPa，与利用解析计算得到的最大复合应力1401.53MPa相吻合，相对偏差仅为0.79%。结果表明，所建立的变厚度节流阀片应力解析计算方法是正确的。

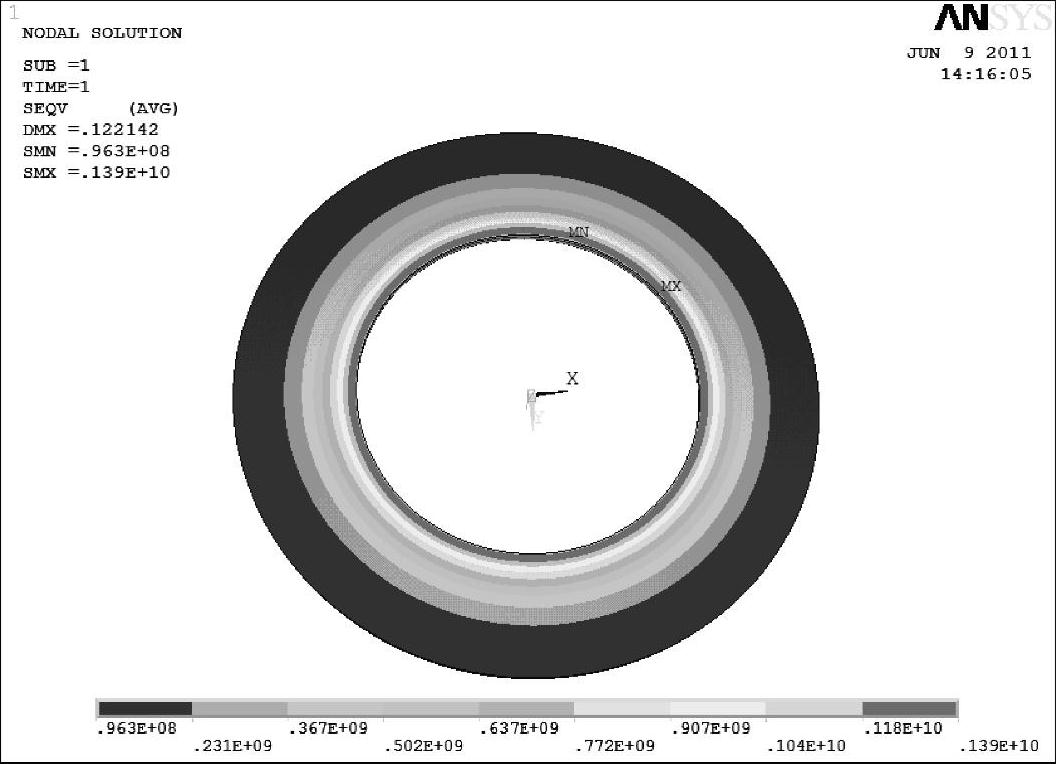
图4-38 阀片变形仿真云图

需要说明的是，对于变厚度节流阀片在非均布压力下及环形集中力下的变形量和应力计算式，同样可以根据变厚度节流阀片转角微分方程，利用边界条件和连续条件求得，这里不再进行求解。