悬架弹性力学解析计算理论

减振器变厚度节流阀片在均布压力下的力学模型如图4-32所示，阀片中间是固定约束，有效内圆半径为r_a，外圆半径为r_b，阀口半径为r_k，变厚度半径为r_t，所受均布压力为p，在半径r处的弯曲变形量为f_r，转角为θ。节流阀片厚度为

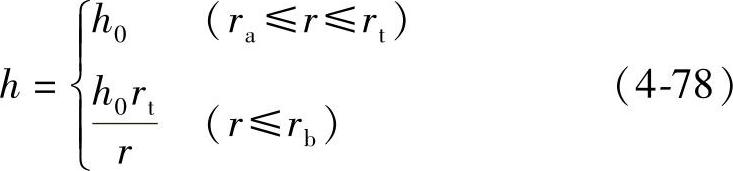
以阀片圆心建立极坐标系，由于载荷和结构绕z轴对称，故根据第3章中式（3-22）可以得到弹性变形转角的微分方程为

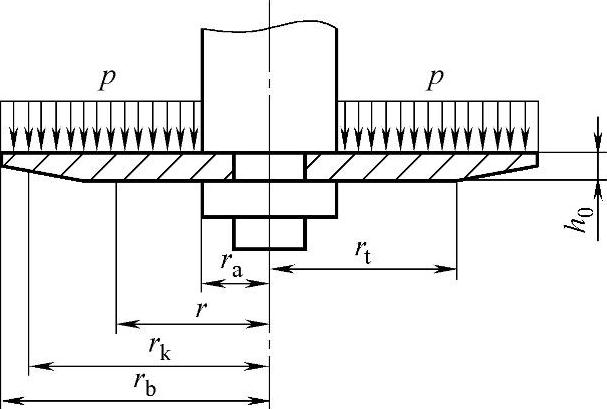
图4-32 变厚度节流阀片在均布压力下的力学模型

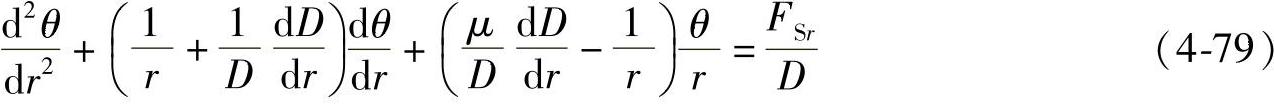
式中，θ为转角且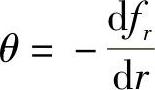（负号表示向下弯曲）；F_Sr为半径r处阀片单位宽度上的剪切力；D为阀片的弯曲刚度且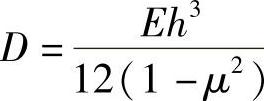；E为阀片的弹性模量；阀片泊松比μ=1/3。

将式（4-78）代入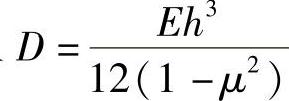，可得阀片在任意半径r处的弯曲刚度为

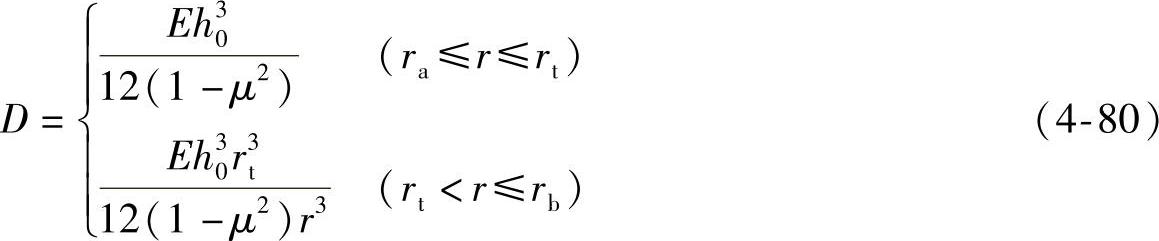
令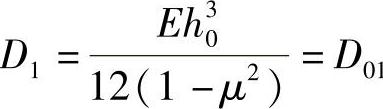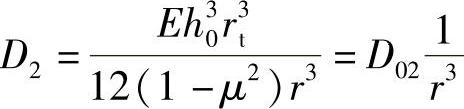，，则式（4-64）化为

在均布压力p的作用下，半径r处的弯矩为

根据式（4-82），可得

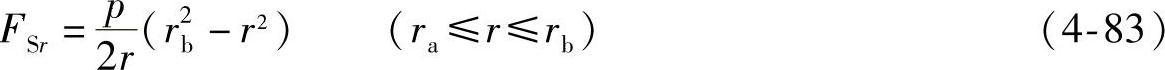
将式（4-81）和式（4-83）代入式（4-79），则曲面的微分方程表示为

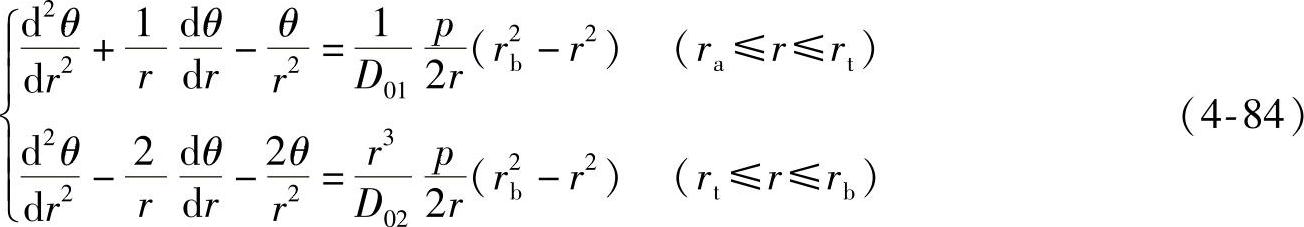
微分方程（4-84）的通解为

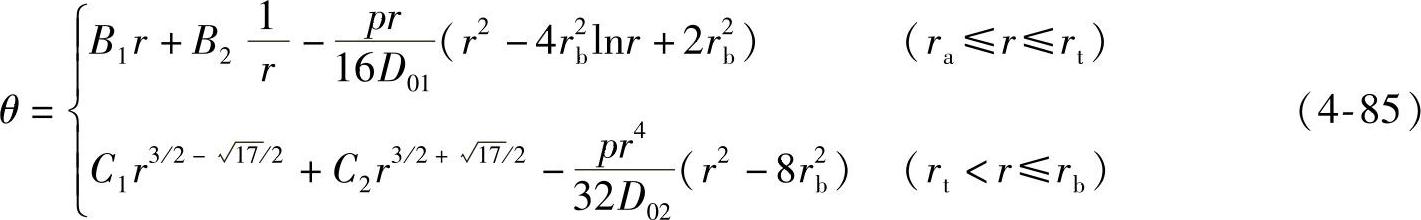
式中，B₁、B₂、C₁和C₂为4个常数，可由节流阀片在内圆和外圆处的边界条件，以及半径r_t处的连续性条件确定，即(https://www.daowen.com)

1）内圆处转角等于零，即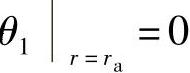，根据通解（4-85），可得

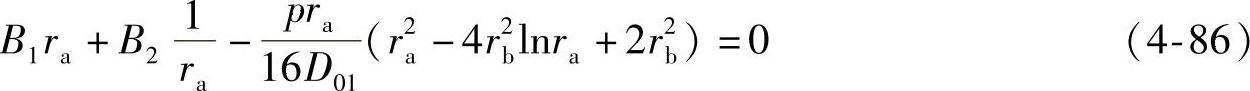
2）外圆处力矩等于零，即M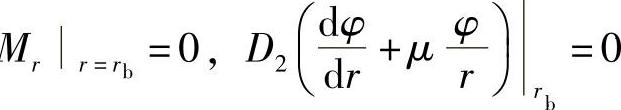，可得

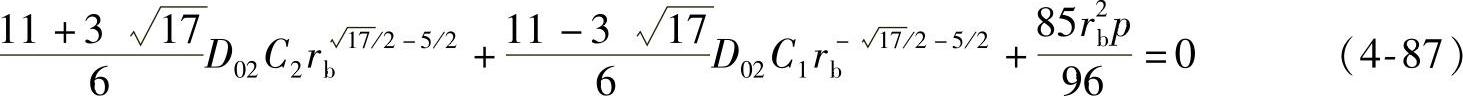
3）阀片半径r_t处的转角相等，即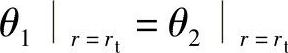，可得

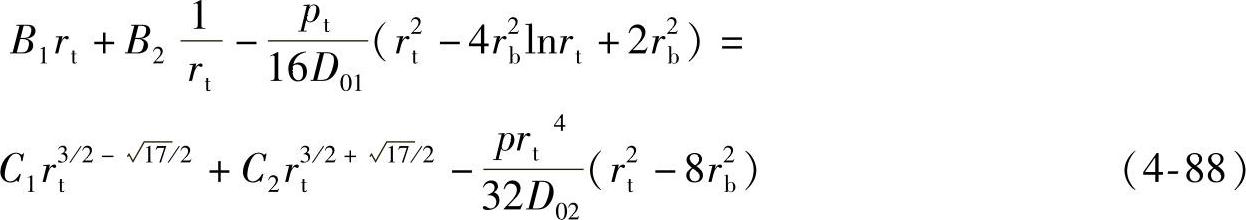
4）阀片在半径r_t处的弯矩相等，即M_1r=r_t=M_2r=r_t，即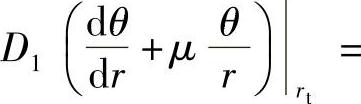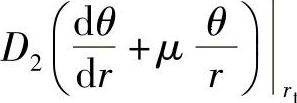,可得

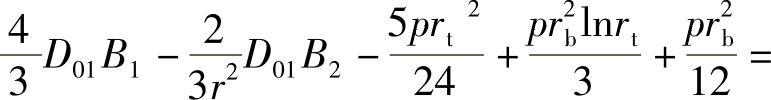
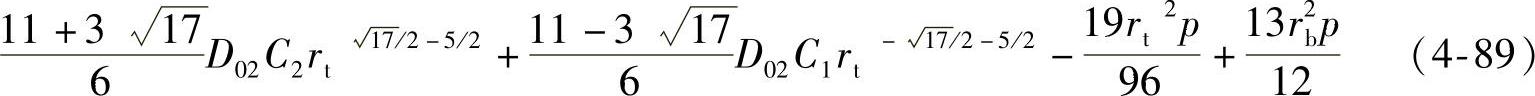
通过联立式（4-86）～式（4-89），可求得变厚度节流阀片在均布载荷作用下的转角微分方程通解的4个常数，即B₁、B₂、C₁和C₂，从而得到均布载荷作用下的节流阀片转角通解表达式。

对转角通解表达式（4-85）求不定积分，得阀片变形通解为

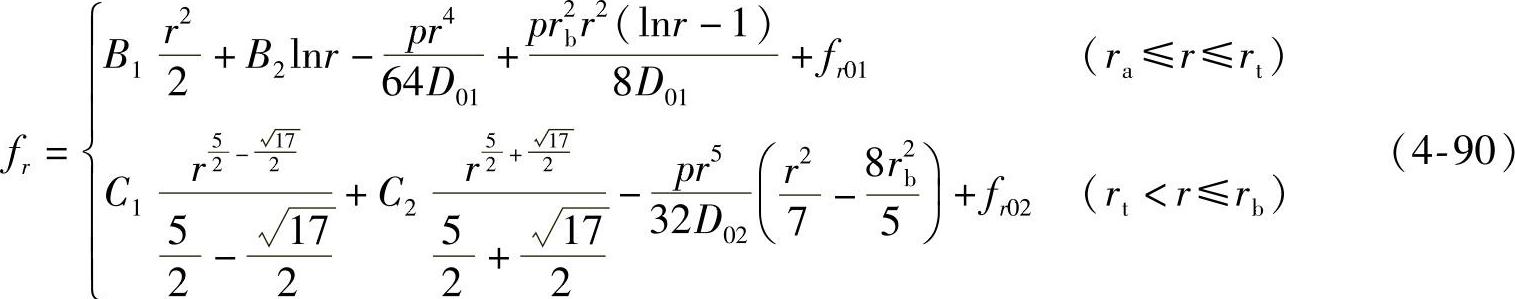
式中，f_r01、f_r02为阀片变形量的特解，可根据边界条件和连续性条件确定，即

1）内圆处变形等于零，即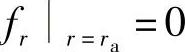，根据阀片变形量通解式（4-79），可得

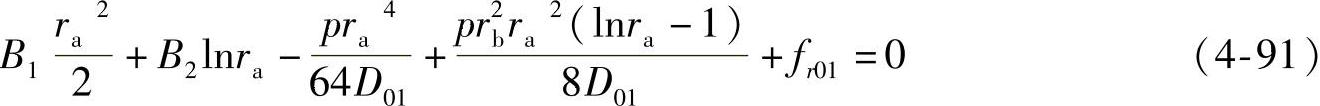
2）阀片半径r_t处的变形量相等，即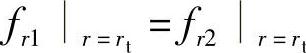，根据阀片变形量通解式（4-79），可得

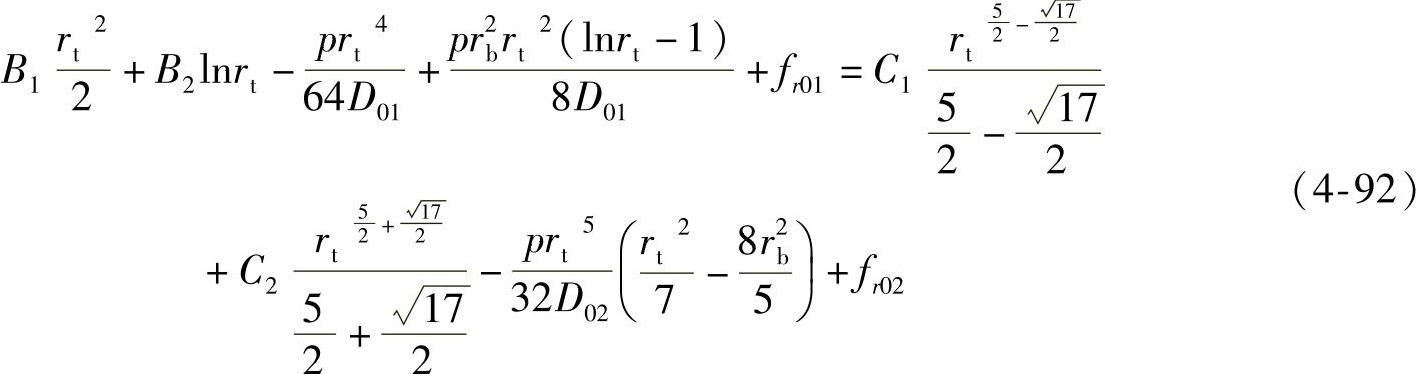
通过联立式（4-90）和式（4-91），可求得变厚度节流阀片变形通解的两个特解，即f_r01和f_r02。