由上述对节流阀片变形量的分析计算可知，利用所求得的阀片变形方程，可以求得在位置半径r处的变形量。但是由于方程解的解析表达式非常复杂，并且还是一个关于半径r的函数表达式，故很难满足阀片设计要求。

在对减振器节流阀片设计时，阀片的内半径r_a、外半径r_b、阀口半径r_k和材料弹性模量E是确定的，需要设计的主要参数是阀片厚度h。

对阀片变形方程的通解分析发现，解的各项常数都含有一个公因子p/h³。对通解进行恒等变换，将各项都化为关于p/h³的表达式，而将阀片的内径r_a、外径r_b、弹性模量E和泊松比_μ以及变形位置半径r都归到一个系数G_r。

根据上述分析，对节流阀片变形方程通解进行恒等变换，则阀片在位置半径r处的变形表达式（4-3）可表示为

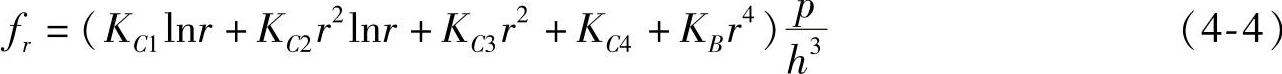
令G_r=K_C1lnr+K_C2r²lnr+K_C3r²+K_C4+K_Br⁴，则式（4-4）可简洁地表示为

(www.daowen.com)

式中，G_r为所定义的阀片在半径r处的变形系数，即阀片变形“长城”系数（是由周长城教授用自己的名字命名的）。

由式（4-4）可知，阀片变形“长城”系数G_r中的各项系数K_C1、K_C2、K_C3、K_C4和K_B是分别由变形方程解的常数C₁、C₂、C₃、C₄和B，在不考虑公因子p/h³的情况下计算求得的。例如，某减振器节流阀片的变形“长城系数”随半径变化的曲线，如图4-2所示。

由图4-2可知，阀片变形“长城”系数G_r与阀片厚度无关，只与阀片的内半径、外半径以及阀片材料的物理特性有关。因此，阀片弯曲变形系数的物理意义是单位阀片厚度h，在单位压力p作用下，在半径r处的弯曲变形能力，其单位为m⁶/N或mm⁶/N。

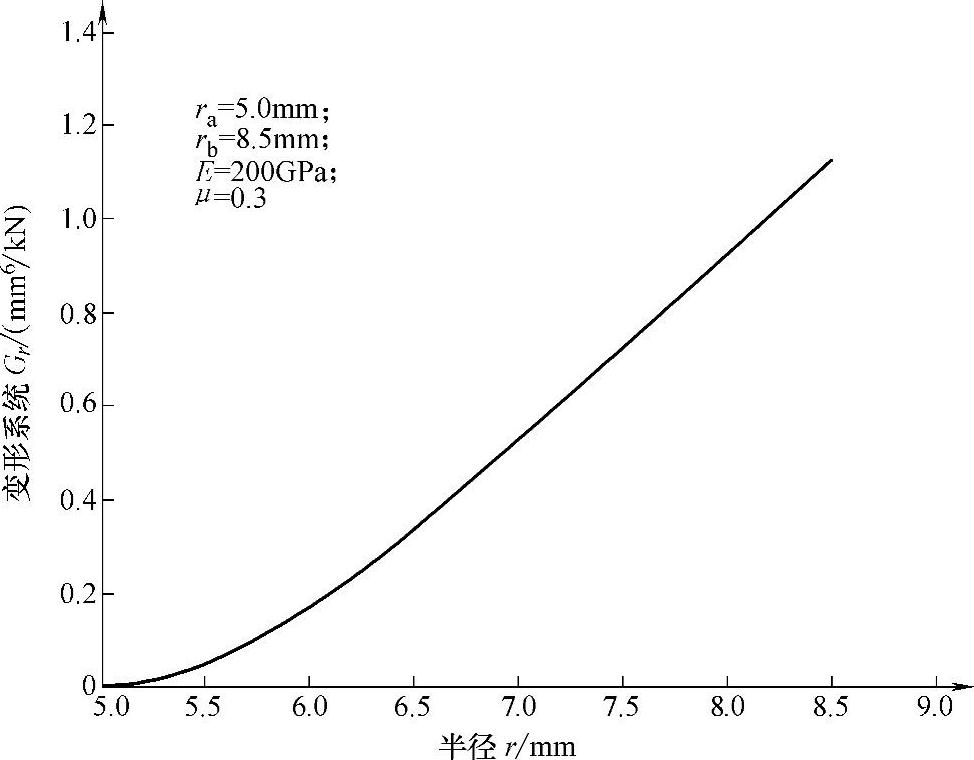
图4-2 阀片变形系数G_r随半径r变换曲线