薄板弯曲问题属于空间问题。为了建立薄板的小挠度弯曲理论，除了引用弹性力学的5个基本假定外，还补充提出了3个计算假定，用来简化空间问题的基本方程（这些计算假定已被大量的实验证实是合理的）。取薄板的中面为xy面，如图3-1所示，薄板的计算假定可以陈述如下：

1）垂直于中面方向的线应变（ε_z）可以忽略不计。取ε_z=0，则由几何方程[式（2-38）]中的第三式得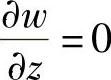，从而得

w=w（x，y）

这就是说，横向位移w只是x和y的函数，不随z而变。因此，在中面的任意一根法线上各点都具有相同的横向位移，也就是挠度。

2）应力分量τ_xz、τ_yz和σ_z远小于其余3个应力分量，因而是次要的，它们所引起的形变可以忽略不计（注意：这3个次要应力分量本身都是维持平衡所必需的，不能不计）。

这是因为，薄板弯曲问题与梁的弯曲问题相似，由各应力分量的数量级大小可知，弯应力σ_x、σ_y和扭应力τ_xy为主要应力，横向的切应力τ_xz、τ_yz为次要应力，而挤压应力σ_z为更次要应力。因此，上述假定中认为τ_xz、τ_yz和σ_z是次要的，它们引起的形变可以忽略不计。

因为不计τ_xz及τ_yz所引起的形变，所以有

γ_zx=0，γ_yz=0

于是由几何方程[式（2-38）]的第四式和第五式可得

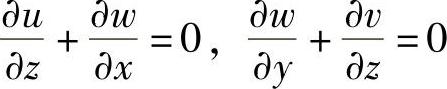
从而有

(www.daowen.com)

由于ε_z=0，γ_xz=0，γ_yz=0，可见中面的法线在薄板弯曲时保持不伸缩，并且成为弹性曲面的法线。

还应注意，在上述计算假定中虽然采用了ε_z=0，γ_zx=0，γ_yz=0，但在以后考虑平衡条件时，仍然必须计入3个次要的应力分量τ_xz、τ_yz和σ_z。因此，在薄板的小挠度弯曲理论中，放弃了关于ε_z、γ_xz和γ_yz的物理方程，即式（2-38）中的第二、第四和第五方程。

因为不计σ_z所引起的形变，所以薄板的物理方程成为

这就是说，薄板小挠度弯问题中的物理方程和薄板平面应力问题中的物理方程是相同的（以后可见，这两种问题中的应力分量和形变分量沿板厚度方向的分量是不同的）。

3）薄板中面内的各点都没有平行于中面的位移，即

（u）_z=0=0，（v）_z=0=0 （3-3）

因为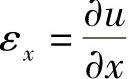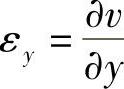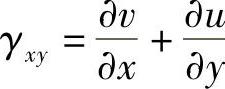，，，所以由式（3-3）得出中面内的形变分量均为零，即

（ε_x）_z=0=0，（ε_y）_z=0=0，（γ_xy）_z=0=0

这就是说，中面的任意一部分，虽然弯曲成为弹性曲面的一部分，但它在xy面上的投影却保持不变。

在材料力学里分析直梁的弯曲问题时，也采用了与以上相似的计算假定，只是在这里，薄板的中面代替了直梁的轴线，薄板的弹性曲面代替了直梁的弹性曲线，薄板的双向弯曲（实际是连弯带扭）代替了直梁的单向弯曲。